
Kaggleのタイタニックの生存予測モデル、精度向上にむけて
はじめに
こんにちは。最近Pythonを用いたデータ分析を学んでいるだはーです。
以前、「データ分析を学び始めて3ヶ月でkaggleのコンペに挑戦してみた。」という記事を投稿し、kaggleのtitnicコンペにチャレンジしました。
データの前処理から特徴量の抽出、予測モデルの選定などを行い、正答率0.82の予測モデルを作成しました。
今回はそこから、より精度の高い予測モデルの作成を目指そうと思います。
分析方針を立てる
以前の内容を振り返りつつ、どのように改善していくかを検討します。
予測モデルの性能を向上させる方法は主に下記の方法が挙げられます。
特徴量を追加する
モデルのアルゴリズムやハイパーパラメータを変更する
複数のモデルを用いてアンサンブルやスタッキングを行う
複数まとめて取り組むと何が原因で性能が向上/悪化したのかが分からなくなってしまうので、1つ1つ検証していきます。
今回は新たな特徴量を作成し、予測モデルの改善に取り組んでいきます。
特徴量は、探索的データ分析(EDA)を行い、そこで得た知見をもとに作成していきます。仮説を立てる→集計・可視化を行い検証のサイクルをまわしていきます。
新たな特徴量の作成と可視化
以前の、各カラムと目的変数との関係の可視化におけるSibSp(兄弟・配偶者の数)とParch(両親・子どもの数)のグラフから、同乗した人数と生存率の間には下記のような関係があることがわかりました。
SibSpのグラフから、同乗した兄弟・配偶者の数が1〜2人の人の生存率が高い
Parchのグラフから、同乗した両親・子どもの数が1〜3人の人の生存率が高い
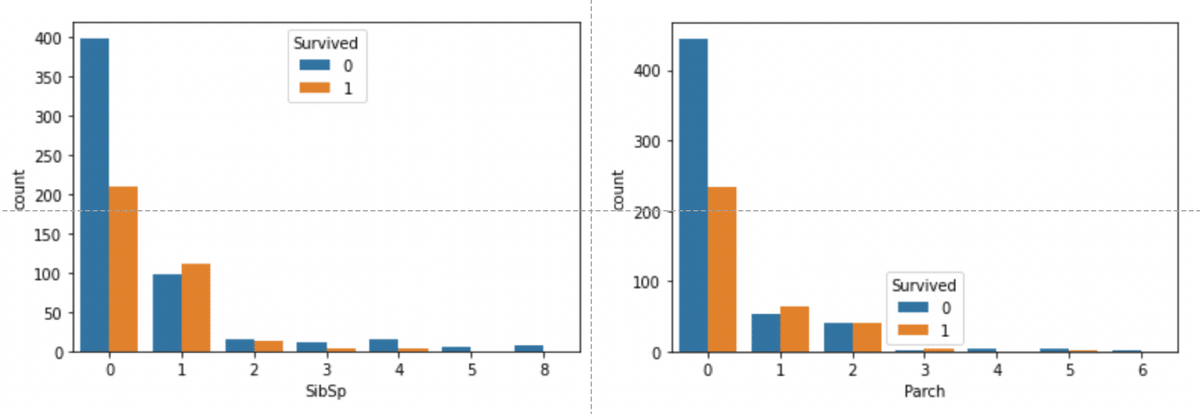
右図、Parchと生存人数の関係
これらをもとに考えると、「同乗した人数と生存率には何かしら関係があるのではないか」という仮説を立てることができます。
仮説を検証するために、「同乗した家族の人数」という新たな特徴量(FamilySize)を作成し、生存率との関係をみてみます。以下のコードで可視化を行います。
#同乗した兄弟姉妹と親子の人数の和をとり、新たな特徴量「同乗した家族の人数」を作成
train_df['FamilySize'] = train_df['SibSp'] + train_df['Parch']
#FamilySizeと生存率の関係を可視化
sns.countplot(
x='FamilySize',
hue='Survived',
data=train_df
)
plt.legend(title='Survived', loc='upper right')
plt.show()
これらのグラフから分かることを以下に記載します。
全体に占める1人で乗船した人の割合は大きいが、その生存率は低い
2〜4人の家族で乗船した場合、生存率は高くなっている
5人以上の家族では、生存率は低くなっている
新たな特徴量について集計
データの可視化で得た知見を確認するために、生存率の割合を家族人数毎で算出してみましょう。
#家族人数毎のデータに含まれる割合
display(train_df['FamilySize'].value_counts(ascending=False, normalize=True))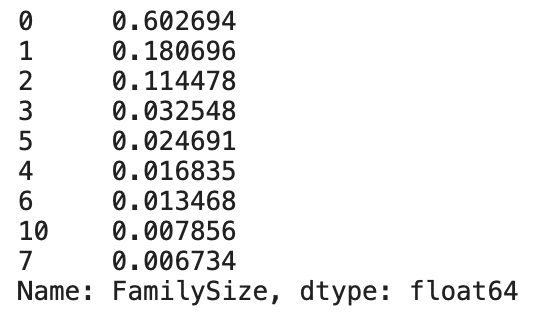
value_countsでデータの値の頻度を計算します。同乗者数が0人の割合が6割以上であることがわかります。
また、家族人数毎の生存率をみてみます。
#家族人数毎の生存率
display(pd.crosstab(train_df['FamilySize'], train_df['Survived'], normalize='index'))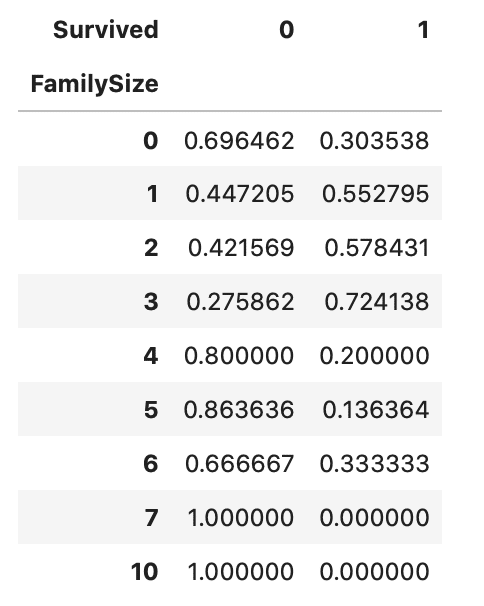
FmilySizeが1〜3、つまり同乗者数が2〜4人の場合の人数に対する生存率の割合が大きいことが分かります。
test_df = pd.read_csv('/kaggle/input/titanic/test.csv')
sample_sub = pd.read_csv('/kaggle/input/titanic/gender_submission.csv')
all_df = pd.concat([train_df,test_df],axis=0).reset_index(drop=True)
all_df['Test_Flag'] = 0
all_df.loc[train_df.shape[0]: , 'Test_Flag'] = 1
all_df['FamilySize'] = all_df['SibSp'] + all_df['Parch'] + 1
display(
all_df['FamilySize'].value_counts(ascending=False,normalize=True)
)
display(pd.crosstab(all_df['FamilySize'], all_df['Survived'], normalize='index'))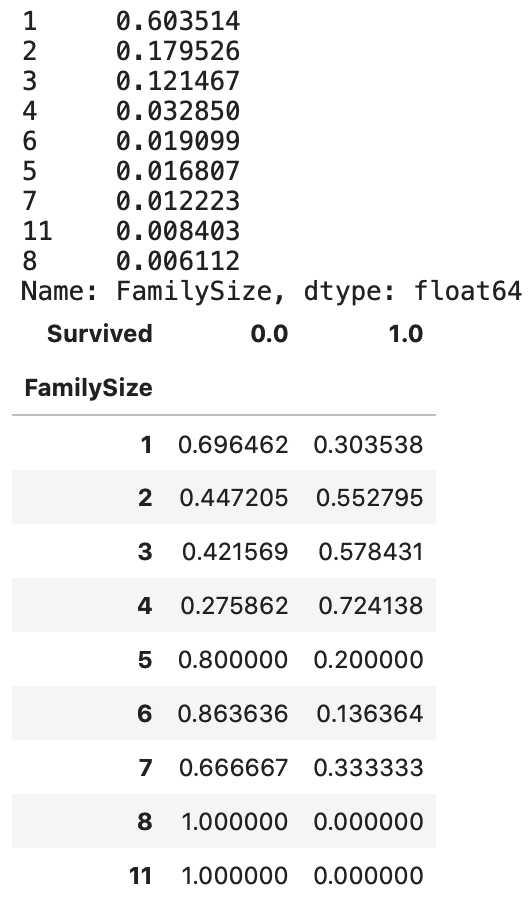
データ全体においても訓練データと同じような割合がみてとれます。
学習データとテストデータのデータの分布が大きく異なる場合は、予測モデルの作成が難しくなるため、双方の分布の確認は意識して行う必要があります。
別の角度からデータを見る
今まで家族人数毎で集計、可視化を行ってきたところを、「1人で乗船した人か2人以上で乗船した人か」に軸を変え、データを眺めてみます。
#1人で乗船した人のカテゴリーを作成
#1人で乗船した人を1、2人以上で乗船した人を0
train_df['Alone'] = train_df['FamilySize'].map(lambda s: 1 if s == 0 else 0)
#「1人で乗船した人か2人以上で乗船した人か」と生存率の関係を可視化
sns.countplot(
x='Alone',
hue='Survived',
data=train_df
)
plt.legend(title='Survived', loc='upper right')
plt.show()上記のコードでは、FamilySizeが0(s==0)の場合に1、それ以外は0とするAloneという新しいカラムをtrain_dfに作成している。
そのカラムAloneと、生存人数との関係を表示している。

この可視化から、一人で乗船する場合は生存率が低いことがわかります。
実際に数値で見てみましょう。
#家族人数毎のデータに含まれる割合を算出
display(pd.crosstab(train_df['Alone'], train_df['Survived'], normalize='index'))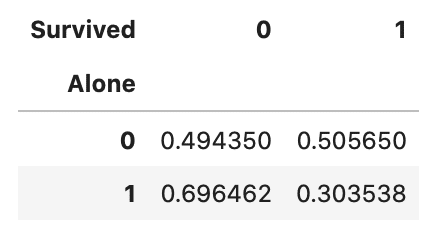
一人で乗船している場合は生存率が0.30、二人以上で乗船している場合は生存率が0.50です。
数値データからも、一人で乗船する場合の生存率が低いことがわかります。
これまでの分析のまとめ
これまでの分析で得られた知見を整理してみます。
1人で乗船した人が全体の約6割で、生存率が3割程度
2〜4人の家族で乗船した割合が全体の約3割で、生存率5割を超えている
5人以上の家族で乗船した割合が全体の約1割で、生存率は1〜3割程度
誰かと同乗した人は、1人で乗船した人と比べ生存率が高い
上記のような知見をもとに新たな特徴量を作成します。
SibSpとParchから新たに「同乗した家族の人数」の特徴量を作成
同乗した家族の人数から、1人、2〜4人、5人以上の3つのカテゴリを作成する
下記のようなコードを記述し、新たなデータセットに追加します。
#CSVファイルからデータを取得
train_df = pd.read_csv('/kaggle/input/titanic/train.csv')
test_df = pd.read_csv('/kaggle/input/titanic/test.csv')
sample_sub = pd.read_csv('/kaggle/input/titanic/gender_submission.csv')
#データ全体にまとめて処理を行うために、訓練データとテストデータを結合
all_df = pd.concat([train_df, test_df], axis=0).reset_index(drop=True)
all_df['Test_Flag'] = 0
all_df.loc[train_df.shape[0]:, 'Test_Flag'] = 1
#Chapter1,3で使用した特徴量作成
all_df['Age'] = all_df['Age'].fillna(all_df['Age'].median())
all_df['Fare'] = all_df['Fare'].fillna(all_df['Fare'].median())
all_df['Embarked'] = all_df['Embarked'].fillna('NaN')
all_df['FareBand'] = pd.qcut(all_df['Fare'], 4)
all_df['AgeBand'] = pd.qcut(all_df['Age'], 4)
#同乗した家族の人数を追加
all_df['FamilySize'] = all_df['SibSp'] + all_df['Parch'] + 1
#同乗した家族の人数をもとに分割
all_df['MedF'] = all_df['FamilySize'].map(lambda s: 1 if 2 <= s <= 4 else 0)
all_df['LargeF'] = all_df['FamilySize'].map(lambda s: 1 if s >= 5 else 0)
#カテゴリカル変数をOne-Hot Encordingで数値化
all_df = pd.get_dummies(all_df, columns= ["Sex", "Pclass"])
all_df = pd.get_dummies(all_df, columns= ["AgeBand", "FareBand", "Embarked"])検証データの作成
特徴量の作成ができたため、加工した訓練データから検証データの作成を行います。
from sklearn.model_selection import train_test_split
#結合していた訓練データとテストデータを元に戻す
train = all_df[all_df['Test_Flag']==0]
test = all_df[all_df['Test_Flag']==1].reset_index(drop=True)
target = train['Survived']
#今回、学習に用いないカラムを削除
drop_col = [
'PassengerId', 'Age',
'Ticket',
'Fare', 'Cabin',
'Test_Flag', 'Name', 'Survived'
]
train = train.drop(drop_col, axis=1)
test = test.drop(drop_col, axis=1)
#訓練データから検証データを作成
X_train, X_val, y_train, y_val = train_test_split(
train, target,
test_size=0.2, shuffle=True, random_state=0
)予測モデルの構築
学習に用いるデータの準備ができたので、予測モデルを構築していきます。今回も前回と同様、生存したかしていないかの2値分類問題なので、ロジスティック回帰を用います。
また、同時に訓練データに対する予測の精度も算出します。
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
#モデルを定義し学習
model = LogisticRegression()
model.fit(X_train, y_train)
#訓練データに対しての予測を行い、正答率を算出
y_pred = model.predict(X_train)
print(accuracy_score(y_train, y_pred))結果は0.8089887640449438でした。
特徴量を改善する前の予測モデルでは、正答率は0.7991573033707865でしたので、多少の精度向上が確認できました。
テストデータへの予測の精度評価
それでは、テストデータに対する予測精度の評価を行いたいと思います。
# 評価用データを予測
y_pred_val = model.predict(X_val)
# 予測結果を正答率で評価
print(accuracy_score(y_val, y_pred_val))結果は0.8212290502793296でした。
特徴量を改善する前の予測モデルでは、テストデータに対する正答率は0.8268156424581006でしたので、精度の向上は確認できませんでした。
まとめ
今回は、予測モデルの特徴量を加工することで精度が向上するかどうかを検証しました。
具体的には、目的変数に対する各カラムの関係性の可視化から「同乗者数と生存率では、同乗者数0人(1人で乗船した場合)よりも、同乗者数1〜3人(2人〜4人で乗船した場合)の方が生存率が高くなるということが分かったため、新たにFamilySizeというカラムを作成し、特徴量に加えました。
その結果、検証データに対する予測精度は向上したものの、テストデータに対する予測精度には向上がみられませんでした。
理由としては、検証の分布と訓練データの分布との差は小さいけれど、検証データの分布とテストデータの分布との差は大きいことが原因の1つだと思われます。
このような場合は、検証方法を見直すことを考えます。検証データの作成をホールドアウト法ではなく、クロスバリデーションを用いて検証するなどです。
訓練データや検証データ、テストデータの分布の差をどのように小さくするのかというのも、今後の考慮するべき対象にしていきたいです。
