ラビットチャレンジ_深層学習day3

Section1:再帰型ニューラルネットワークの概念

 1-1:要点
　・RNN(リカレントニューラルネットワーク)とは、時系列データに
　　対応可能なニューラルネットワークである
　　⇒時系列データ例：音声、テキストなど
　・特徴：過去の中間層の出力を次の中間層に入力として与えてあげる
　　⇒過去の情報を反映した学習が行える
　　⇒下図のZ1→Z2に入力している部分が過去の情報
　　　⇒時系列モデルを扱には、初期の状態と過去の時間t-1の状態を保持　　
　　　　し、そこから次の時間でのtを再起的に求める再起構造が必要となる

　・BPTTとは、RNNにおいてのパラメータ調整方法の一種
　　⇒誤差逆伝播の一種

1-2:実装演習
・バイナリ計算を学習させるコード

import numpy as np
from common import functions
import matplotlib.pyplot as plt

# def d_tanh(x):

# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)

input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1

weight_init_std = 1
learning_rate = 0.1

iters_num = 10000
plot_interval = 100

# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)

# Xavier


# He

# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)

u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))

delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))

all_losses = []

for i in range(iters_num):
   
   # A, B初期化 (a + b = d)
   a_int = np.random.randint(largest_number/2)
   a_bin = binary[a_int] # binary encoding
   b_int = np.random.randint(largest_number/2)
   b_bin = binary[b_int] # binary encoding
   
   # 正解データ
   d_int = a_int + b_int
   d_bin = binary[d_int]
   
   # 出力バイナリ
   out_bin = np.zeros_like(d_bin)
   
   # 時系列全体の誤差
   all_loss = 0    
   
   # 時系列ループ
   for t in range(binary_dim):
       # 入力値
       X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
       # 時刻tにおける正解データ
       dd = np.array([d_bin[binary_dim - t - 1]])
       
       u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
       z[:,t+1] = functions.sigmoid(u[:,t+1])

       y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))


       #誤差
       loss = functions.mean_squared_error(dd, y[:,t])
       
       delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])        
       
       all_loss += loss

       out_bin[binary_dim - t - 1] = np.round(y[:,t])
   
   
   for t in range(binary_dim)[::-1]:
       X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)        

       delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])

       # 勾配更新
       W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
       W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
       W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
   
   # 勾配適用
   W_in -= learning_rate * W_in_grad
   W_out -= learning_rate * W_out_grad
   W -= learning_rate * W_grad
   
   W_in_grad *= 0
   W_out_grad *= 0
   W_grad *= 0
   

   if(i % plot_interval == 0):
       all_losses.append(all_loss)        
       print("iters:" + str(i))
       print("Loss:" + str(all_loss))
       print("Pred:" + str(out_bin))
       print("True:" + str(d_bin))
       out_int = 0
       for index,x in enumerate(reversed(out_bin)):
           out_int += x * pow(2, index)
       print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
       print("------------")

lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()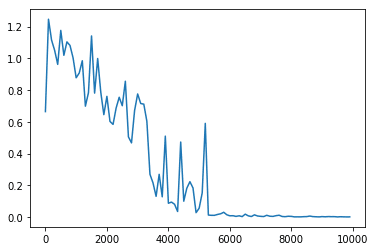

　⇒6000回ぐらい学習したところでほぼ誤差はなくなっていることが分かる

　補足：重みの初期化をHeに変更した結果

　⇒5000回ぐらい学習したところでほぼ誤差はなくなっている
　　⇒ランダムに初期化するよりも早く学習ができている

　補足：中間層の活性化関数をReLU関数に変更

　⇒勾配爆発が起こっていることが分かる
　　※勾配爆発とは
　　　勾配が大きくなりすぎてコンピューターが処理できなくなること

1-3:確認問題
 1.Q

 1.A
　過去の中間層から現在の中間層を定義する際にかけられる重み。
　⇒過去の中間層から現在の中間層への入力が時系列データの過去の情報
　　となっている。

1-4:演習問題
1.Q

1.A (2)
⇒表現ベクトルを作成するプログラムが答えとなるため(2)である

2.Q

2.A (2)

Section2:LSTM

　2-1:要点
　　・RNNでは時系列を遡るほど勾配が消失していく問題がある
　　　LSTMは勾配消失問題を解決できるようにRNNの構造を改良したもの
　　・LSTMの全体像

　・CEC 
　　これまでの入力値や中間層の出力を記憶することのみを行うための機能
　　CECの課題：記憶のみしかしないため学習できない(学習特性がない)
　・入力ゲート
　　今回の入力値と前回の出力値を元に今回の入力値をどのように使用する
　　かを決める
　　今回の入力値と前回の出力値をどのぐらい覚えさせるかの重み(W,U)を
　　学習する
　・出力ゲート
　　今回の入力値と前回の出力値からどんなふうにCECのデータを
　　使えば良いかを決める
　・忘却ゲート
　　CECは、過去の情報を全て保管されている
　　過去の情報が要らなくなった場合に削除することができず残ってしまう
　　⇒過去の情報が要らなくなったら削除するのが忘却ゲートの役割
　・除き穴結合
　　CEC自身の値に、重み行列を介して伝播可能にした構造
　⇒LSTMは複雑になりすぎてしまい計算負荷が大きくあまりよくなかった　

　2-2:実装演習
　Section3のGRUと同時に確認する

　2-3:確認問題
　1.Q

　1.A (2)

　2.Q

   2.A　忘却ゲート

　2-4:演習問題
　1.Q　

　1.A (1)
　⇒クリッピングした勾配 = 勾配 * (閾値 / 勾配ノルム)で計算される

　2.Q

　2.A  (3)
　⇒新しいセルの状態は、計算されたセルへの入力と1ステップ前のセルの　
　　状態に入力ゲート、忘却ゲートを掛けて足し合わせたものである

Section3:GRU

　3-1:要点
　・LSTMではパラメータ数が多く存在し、計算に負荷が大きかったため、
　　少し簡略化したものがGRU

　・リセットゲート：隠れ層の状態をどのように制御するかを決める
　・更新ゲート：どのように覚えている内容を使うかを決める
　⇒2つのゲートで入力ゲート、忘却ゲート、出力ゲートの3つの役割を
　　満たしている

　3-2:実装演習

import tensorflow as tf
import numpy as np
import re
import glob
import collections
import random
import pickle
import time
import datetime
import os

# logging levelを変更
tf.logging.set_verbosity(tf.logging.ERROR)

class Corpus:
   def __init__(self):
       self.unknown_word_symbol = "<???>" # 出現回数の少ない単語は未知語として定義しておく
       self.unknown_word_threshold = 3 # 未知語と定義する単語の出現回数の閾値
       self.corpus_file = "./corpus/**/*.txt"
       self.corpus_encoding = "utf-8"
       self.dictionary_filename = "./data_for_predict/word_dict.dic"
       self.chunk_size = 5
       self.load_dict()

       words = []
       for filename in glob.glob(self.corpus_file, recursive=True):
           with open(filename, "r", encoding=self.corpus_encoding) as f:

               # word breaking
               text = f.read()
               # 全ての文字を小文字に統一し、改行をスペースに変換
               text = text.lower().replace("\n", " ")
               # 特定の文字以外の文字を空文字に置換する
               text = re.sub(r"[^a-z '\-]", "", text)
               # 複数のスペースはスペース一文字に変換
               text = re.sub(r"[ ]+", " ", text)

               # 前処理： '-' で始まる単語は無視する
               words = [ word for word in text.split() if not word.startswith("-")]


       self.data_n = len(words) - self.chunk_size
       self.data = self.seq_to_matrix(words)

   def prepare_data(self):
       """
       訓練データとテストデータを準備する。
       data_n = ( text データの総単語数 ) - chunk_size
       input: (data_n, chunk_size, vocabulary_size)
       output: (data_n, vocabulary_size)
       """

       # 入力と出力の次元テンソルを準備
       all_input = np.zeros([self.chunk_size, self.vocabulary_size, self.data_n])
       all_output = np.zeros([self.vocabulary_size, self.data_n])

       # 準備したテンソルに、コーパスの one-hot 表現(self.data) のデータを埋めていく
       # i 番目から ( i + chunk_size - 1 ) 番目までの単語が１組の入力となる
       # このときの出力は ( i + chunk_size ) 番目の単語
       for i in range(self.data_n):
           all_output[:, i] = self.data[:, i + self.chunk_size] # (i + chunk_size) 番目の単語の one-hot ベクトル
           for j in range(self.chunk_size):
               all_input[j, :, i] = self.data[:, i + self.chunk_size - j - 1]

       # 後に使うデータ形式に合わせるために転置を取る
       all_input = all_input.transpose([2, 0, 1])
       all_output = all_output.transpose()

       # 訓練データ：テストデータを 4 : 1 に分割する
       training_num = ( self.data_n * 4 ) // 5
       return all_input[:training_num], all_output[:training_num], all_input[training_num:], all_output[training_num:]


   def build_dict(self):
       # コーパス全体を見て、単語の出現回数をカウントする
       counter = collections.Counter()
       for filename in glob.glob(self.corpus_file, recursive=True):
           with open(filename, "r", encoding=self.corpus_encoding) as f:

               # word breaking
               text = f.read()
               # 全ての文字を小文字に統一し、改行をスペースに変換
               text = text.lower().replace("\n", " ")
               # 特定の文字以外の文字を空文字に置換する
               text = re.sub(r"[^a-z '\-]", "", text)
               # 複数のスペースはスペース一文字に変換
               text = re.sub(r"[ ]+", " ", text)

               # 前処理： '-' で始まる単語は無視する
               words = [word for word in text.split() if not word.startswith("-")]

               counter.update(words)

       # 出現頻度の低い単語を一つの記号にまとめる
       word_id = 0
       dictionary = {}
       for word, count in counter.items():
           if count <= self.unknown_word_threshold:
               continue

           dictionary[word] = word_id
           word_id += 1
       dictionary[self.unknown_word_symbol] = word_id

       print("総単語数：", len(dictionary))

       # 辞書を pickle を使って保存しておく
       with open(self.dictionary_filename, "wb") as f:
           pickle.dump(dictionary, f)
           print("Dictionary is saved to", self.dictionary_filename)

       self.dictionary = dictionary

       print(self.dictionary)

   def load_dict(self):
       with open(self.dictionary_filename, "rb") as f:
           self.dictionary = pickle.load(f)
           self.vocabulary_size = len(self.dictionary)
           self.input_layer_size = len(self.dictionary)
           self.output_layer_size = len(self.dictionary)
           print("総単語数: ", self.input_layer_size)

   def get_word_id(self, word):
       # print(word)
       # print(self.dictionary)
       # print(self.unknown_word_symbol)
       # print(self.dictionary[self.unknown_word_symbol])
       # print(self.dictionary.get(word, self.dictionary[self.unknown_word_symbol]))
       return self.dictionary.get(word, self.dictionary[self.unknown_word_symbol])

   # 入力された単語を one-hot ベクトルにする
   def to_one_hot(self, word):
       index = self.get_word_id(word)
       data = np.zeros(self.vocabulary_size)
       data[index] = 1
       return data

   def seq_to_matrix(self, seq):
       print(seq)
       data = np.array([self.to_one_hot(word) for word in seq]) # (data_n, vocabulary_size)
       return data.transpose() # (vocabulary_size, data_n)

class Language:
   """
   input layer: self.vocabulary_size
   hidden layer: rnn_size = 30
   output layer: self.vocabulary_size
   """

   def __init__(self):
       self.corpus = Corpus()
       self.dictionary = self.corpus.dictionary
       self.vocabulary_size = len(self.dictionary) # 単語数
       self.input_layer_size = self.vocabulary_size # 入力層の数
       self.hidden_layer_size = 30 # 隠れ層の RNN ユニットの数
       self.output_layer_size = self.vocabulary_size # 出力層の数
       self.batch_size = 128 # バッチサイズ
       self.chunk_size = 5 # 展開するシーケンスの数。c_0, c_1, ..., c_(chunk_size - 1) を入力し、c_(chunk_size) 番目の単語の確率が出力される。
       self.learning_rate = 0.005 # 学習率
       self.epochs = 1000 # 学習するエポック数
       self.forget_bias = 1.0 # LSTM における忘却ゲートのバイアス
       self.model_filename = "./data_for_predict/predict_model.ckpt"
       self.unknown_word_symbol = self.corpus.unknown_word_symbol

   def inference(self, input_data, initial_state):
       """
       :param input_data: (batch_size, chunk_size, vocabulary_size) 次元のテンソル
       :param initial_state: (batch_size, hidden_layer_size) 次元の行列
       :return:
       """
       # 重みとバイアスの初期化
       hidden_w = tf.Variable(tf.truncated_normal([self.input_layer_size, self.hidden_layer_size], stddev=0.01))
       hidden_b = tf.Variable(tf.ones([self.hidden_layer_size]))
       output_w = tf.Variable(tf.truncated_normal([self.hidden_layer_size, self.output_layer_size], stddev=0.01))
       output_b = tf.Variable(tf.ones([self.output_layer_size]))

       # BasicLSTMCell, BasicRNNCell は (batch_size, hidden_layer_size) が chunk_size 数ぶんつながったリストを入力とする。
       # 現時点での入力データは (batch_size, chunk_size, input_layer_size) という３次元のテンソルなので
       # tf.transpose や tf.reshape などを駆使してテンソルのサイズを調整する。

       input_data = tf.transpose(input_data, [1, 0, 2]) # 転置。(chunk_size, batch_size, vocabulary_size)
       input_data = tf.reshape(input_data, [-1, self.input_layer_size]) # 変形。(chunk_size * batch_size, input_layer_size)
       input_data = tf.matmul(input_data, hidden_w) + hidden_b # 重みWとバイアスBを適用。 (chunk_size, batch_size, hidden_layer_size)
       input_data = tf.split(input_data, self.chunk_size, 0) # リストに分割。chunk_size * (batch_size, hidden_layer_size)

       # RNN のセルを定義する。RNN Cell の他に LSTM のセルや GRU のセルなどが利用できる。
       cell = tf.nn.rnn_cell.BasicRNNCell(self.hidden_layer_size)
       outputs, states = tf.nn.static_rnn(cell, input_data, initial_state=initial_state)
       
       # 最後に隠れ層から出力層につながる重みとバイアスを処理する
       # 最終的に softmax 関数で処理し、確率として解釈される。
       # softmax 関数はこの関数の外で定義する。
       output = tf.matmul(outputs[-1], output_w) + output_b

       return output

   def loss(self, logits, labels):
       cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels))

       return cost

   def training(self, cost):
       # 今回は最適化手法として Adam を選択する。
       # ここの AdamOptimizer の部分を変えることで、Adagrad, Adadelta などの他の最適化手法を選択することができる
       optimizer = tf.train.AdamOptimizer(learning_rate=self.learning_rate).minimize(cost)

       return optimizer

   def train(self):
       # 変数などの用意
       input_data = tf.placeholder("float", [None, self.chunk_size, self.input_layer_size])
       actual_labels = tf.placeholder("float", [None, self.output_layer_size])
       initial_state = tf.placeholder("float", [None, self.hidden_layer_size])

       prediction = self.inference(input_data, initial_state)
       cost = self.loss(prediction, actual_labels)
       optimizer = self.training(cost)
       correct = tf.equal(tf.argmax(prediction, 1), tf.argmax(actual_labels, 1))
       accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

       # TensorBoard で可視化するため、クロスエントロピーをサマリーに追加
       tf.summary.scalar("Cross entropy: ", cost)
       summary = tf.summary.merge_all()

       # 訓練・テストデータの用意
       # corpus = Corpus()
       trX, trY, teX, teY = self.corpus.prepare_data()
       training_num = trX.shape[0]

       # ログを保存するためのディレクトリ
       timestamp = time.time()
       dirname = datetime.datetime.fromtimestamp(timestamp).strftime("%Y%m%d%H%M%S")

       # ここから実際に学習を走らせる
       with tf.Session() as sess:
           sess.run(tf.global_variables_initializer())
           summary_writer = tf.summary.FileWriter("./log/" + dirname, sess.graph)

           # エポックを回す
           for epoch in range(self.epochs):
               step = 0
               epoch_loss = 0
               epoch_acc = 0

               # 訓練データをバッチサイズごとに分けて学習させる (= optimizer を走らせる)
               # エポックごとの損失関数の合計値や（訓練データに対する）精度も計算しておく
               while (step + 1) * self.batch_size < training_num:
                   start_idx = step * self.batch_size
                   end_idx = (step + 1) * self.batch_size

                   batch_xs = trX[start_idx:end_idx, :, :]
                   batch_ys = trY[start_idx:end_idx, :]

                   _, c, a = sess.run([optimizer, cost, accuracy],
                                      feed_dict={input_data: batch_xs,
                                                 actual_labels: batch_ys,
                                                 initial_state: np.zeros([self.batch_size, self.hidden_layer_size])
                                                 }
                                      )
                   epoch_loss += c
                   epoch_acc += a
                   step += 1

               # コンソールに損失関数の値や精度を出力しておく
               print("Epoch", epoch, "completed ouf of", self.epochs, "-- loss:", epoch_loss, " -- accuracy:",
                     epoch_acc / step)

               # Epochが終わるごとにTensorBoard用に値を保存
               summary_str = sess.run(summary, feed_dict={input_data: trX,
                                                          actual_labels: trY,
                                                          initial_state: np.zeros(
                                                              [trX.shape[0],
                                                               self.hidden_layer_size]
                                                          )
                                                          }
                                      )
               summary_writer.add_summary(summary_str, epoch)
               summary_writer.flush()

           # 学習したモデルも保存しておく
           saver = tf.train.Saver()
           saver.save(sess, self.model_filename)

           # 最後にテストデータでの精度を計算して表示する
           a = sess.run(accuracy, feed_dict={input_data: teX, actual_labels: teY,
                                             initial_state: np.zeros([teX.shape[0], self.hidden_layer_size])})
           print("Accuracy on test:", a)


   def predict(self, seq):
       """
       文章を入力したときに次に来る単語を予測する
       :param seq: 予測したい単語の直前の文字列。chunk_size 以上の単語数が必要。
       :return:
       """

       # 最初に復元したい変数をすべて定義してしまいます
       tf.reset_default_graph()
       input_data = tf.placeholder("float", [None, self.chunk_size, self.input_layer_size])
       initial_state = tf.placeholder("float", [None, self.hidden_layer_size])
       prediction = tf.nn.softmax(self.inference(input_data, initial_state))
       predicted_labels = tf.argmax(prediction, 1)

       # 入力データの作成
       # seq を one-hot 表現に変換する。
       words = [word for word in seq.split() if not word.startswith("-")]
       x = np.zeros([1, self.chunk_size, self.input_layer_size])
       for i in range(self.chunk_size):
           word = seq[len(words) - self.chunk_size + i]
           index = self.dictionary.get(word, self.dictionary[self.unknown_word_symbol])
           x[0][i][index] = 1
       feed_dict = {
           input_data: x, # (1, chunk_size, vocabulary_size)
           initial_state: np.zeros([1, self.hidden_layer_size])
       }

       # tf.Session()を用意
       with tf.Session() as sess:
           # 保存したモデルをロードする。ロード前にすべての変数を用意しておく必要がある。
           saver = tf.train.Saver()
           saver.restore(sess, self.model_filename)

           # ロードしたモデルを使って予測結果を計算
           u, v = sess.run([prediction, predicted_labels], feed_dict=feed_dict)

           keys = list(self.dictionary.keys())


           # コンソールに文字ごとの確率を表示
           for i in range(self.vocabulary_size):
               c = self.unknown_word_symbol if i == (self.vocabulary_size - 1) else keys[i]
               print(c, ":", u[0][i])

           print("Prediction:", seq + " " + ("<???>" if v[0] == (self.vocabulary_size - 1) else keys[v[0]]))

       return u[0]


def build_dict():
   cp = Corpus()
   cp.build_dict()

if __name__ == "__main__":
   #build_dict()

   ln = Language()

   # 学習するときに呼び出す
   #ln.train()

   # 保存したモデルを使って単語の予測をする
   ln.predict("some of them looks like")

急に難しくなった...
ここまでくるとプログラムも複雑になり始め理解するのに時間がかかる...

3-3:確認問題
　1.Q

　1.A LSTMは、計算負荷が大きすぎるため学習に時間がかかること
　　  CECは、勾配がなく学習性能がないこと

　2.Q

　2.A LSTMは入力ゲート、CEC、出力ゲートと呼ばれる3つの機能によって学習を行っていく。GRUは、リセットゲートと忘却ゲートの2つの機能を使って学習を行う。性能面ではLSTMよりGRUの方が計算コストが低いという点が異なる。

3-4:演習問題
1.Q

1.A (4)

　⇒全体像の上記の数式の計算を行うプログラムが答えとなる

Section4:双方向RNN

　4-1:要点
　・過去の情報だけでなく、未来の情報を加味することで、
　　精度を向上させるためのモデル
　　⇒機械には学習データが一気に与えられるため未来のデータにも
　　　アクセスすることができる
　・利用例：文章の推敲や、機械翻訳

　4-2:実装演習
　なし
　4-3:確認問題
　なし

　4-4:演習問題
　1.Q

　1.A (4)　

Section5:Seq2Seq

　5-1:要点
　・入力が時系列なら出力も時系列で予測したいという問題から開発された
　・Encoder-Decoderモデルの一種で機械翻訳の分野で扱われている

　・Encoder:入力データを処理して符号化する

　　・Taking :文章を単語等のトークン毎に分割し、トークンごとのIDに
　　　　　　 分割する。
　　・Embedding :IDから、そのトークンを表す分散表現ベクトルに変換。
　　処理1）vec1をRNNに入力し、hidden stateを出力。
　　　　　このhiddenstateと次の入力vec2をまたRNNに入力してきた
　　　　　hidden stateを出力という流れを繰り返す。
　　処理2）最後のvecを入れたときのhiddenstateをfinalstateとしてとってお 　　　　　く。このfinalstateがthoughtvectorと呼ばれ、入力した文の意味を
　　　　　表すベクトルとなる。

　・Decoder: 符号化された入力情報を使って複合化する

　　処理1)　Encoderのfinal state (thought vector) から、各token の生成確率　　
　　　　　　を出力する。final state をDecoderのinitial state ととして設定
　　　　　　し、Embedding を入力。
　　処理2）Sampling:生成確率にもとづいてtoken をランダムに選ぶ
　　処理3）Embedding:2で選ばれたtoken をEmbedding してDecoder への
　　　　　　次の入力とします
　　処理4）1 -3 を繰り返し、2で得られたtoken を文字列に直します。

　　・Seq2seq2の課題
　　　・一問一答しかできない。
　　　　問に対して文脈も何もなく、ただ応答が行われる続ける。
　　　⇒対策としてHREDの構造が開発された
　　・HRED:前の単語の流れに即して応答される
　　　⇒HREDの課題：ありきたりの回答しかできなかった
　　　⇒対策としてVHRDの構造が開発された
　　・VHRD:HREDに、VAEの潜在変数の概念を追加したもの
　　　　　　より会話に近い回答ができるようになった
　　
　　・オートエンコーダ
　　　教師なし学習の1つ。EncoderとDecoderをもつ
　　　Encoder:入力データから潜在変数zに変換するニューラルネットワーク
　　　Decoder:潜在変数zをインプットとして元画像を復元する
　　　　　　　ニューラルネットワーク
　　　メリット：次元削減が行える
　　　・画像の特徴量を取り出して次元削減する方法と
　　　　次元削減したものから元の画像に戻す方法を学習する。
　　・VAE
　　　通常のオートエンコードの場合、何かしら潜在変数zにデータを押し
　　　込めているものの、その構造がどうような状態かわからない
　　⇒VAEは潜在変数zに確率分布z~N8(0,1)を仮定したもの(正規化したもの)　　　
　　　「1」と「7」のように構造が似ているものはzの値も近くなり
　　　「1」と「2」のように構造が遠いものはzの値が遠くなるようにする

　5-2:実装演習
　なし

　5-3:確認問題
　1.Q

　1.A　(2)

　2.Q

　2.A
  Seq2seqとHREDの違いは、過去の文の情報も加味して出力をするかどうか
HREDとVHREDの違いは、当たり障りのない文章しか回答できないかより人間の会話に近い回答ができるかどうか

　3.Q

　3.A 確率分布

　5-4:演習問題
　1.Q

　1.A (1) 
　⇒特徴量に変換するために重みを掛けてあげればいい

Section6:Word2vec

　6-1:要点
　・単語をベクトル表現する方法
　　⇒One-hotベクトルでは単語の数だけOne-hotベクトルを作り出すため
　　　無駄が多い
　　⇒One-hotベクトルをenbedding表現に変換する手法をWord2vecという
　　　⇒enbedding表現は特徴量を抽出した小さなベクトル

　6-2:実装演習
　なし

　6-3:確認問題
　なし

　6-4:関連記事レポート
　word2vecは、「単語の意味は、その周辺の単語によって決まる」という分布仮説と呼ばれる言語学の主張をニューラルネットワークとして表現したものである。
　word2vecにはスキップグラムとCBOWという2つの手法がある
　スキップグラム：ある単語を与えて周辺の言語を予測するモデル
　CBOW：周辺の単語を与えてある単語を予測するモデル
　⇒入力が1つで出力が複数個か入力が複数個で出力が1つかの違いがある

Section7:Attention Mechanism

　7-1:要点
　・seq2seqの問題は長い文章への対応ができない
　　seq2seqでは、2単語でも100単語でも固定次元ベクトルの中に
　　入力する必要がある
　　⇒Attention Mechanismは入力と出力のどの単語が関連しているかを学習する仕組み

　7-2:実装演習
　なし

　7-3:確認問題
　1.Q

　1.A
　RNNは時系列データを処理するのに便利な手法でり、
　word2vecは単語の分散ベクトルを得る手法である
　seq2seqは1つの時系列データから別の時系列データを得るネットワーク　
　で、Attentionは、時系列データの関連性に重みを付ける手法である