データ分析(1-2) 共分散、相関係数
二次元データの数値的要約です。先にこれについてやる前に散布図について軽く述べます。
二次元データ(Xi, Yi)を平面の上にプロットしたものが散布図です。

(散布図の例)
二つの変数間の関係を相関関係と呼ぶ。特に直線的な傾きがある時、相関があると言う。正の傾きであれば正の相関を持ち, 負の傾きであれば負の相関と呼ぶ。
共分散
二次元データ(Xi, Yi)の共分散をCovとすると次のように書ける。
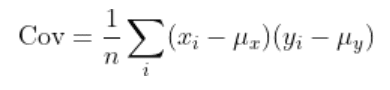
共分散は二つのデータの関係性の強さを表している。

上の図を見ると(Xi-μ_x)*(Yi-μ_y)は赤の領域では正となる。
また、(Xi-μ_x)*(Yi-μ_y)は青の領域では負となる。つまり共分散Covが正であるならばデータは正の相関を持ち、負であるならば負の相関を持つ。
相関係数
共分散はデータの相関が分かると言っても単位が存在するため、単位が変化するとその値も変わってしまう。単位の次元を消すことが目標である。そのため次のように相関係数S_xyを定義する。

S_x、S_yはそれぞれx,yの標準偏差である。この時相関係数S_xyは単位がなくなり扱いやすくなる。
標準偏差についてはこちらを参照してください。
(https://note.com/karaage_love/n/n6f617d38c528#q0JJ8)
相関係数は次のような特徴がある。
1. 相関係数は-1以上1以下
2. 相関係数が正ならば正の相関。1に近いほどより強い正の相関
3. 相関係数が負ならば負の相関。-1に近いほどより強い負の相関
4. 相関係数が0であってもデータ間に関係性がないとは言い切れない。
(例)

上の図の様な関係がある時、相関係数はゼロである。しかし、これにはデータの関係性がないとは言えないであろう。
このような二次元データに対する要約法がある。二次元データは様々な所で用いられている。そのため、いろいろな人が都合の良いようにデータを見せることも多い。だからこそ、私達もそのデータのまとめ方が正しいのかを見極めないと変な奴らに騙されてしまうのである。
