CMA-債券投資

デュレーションとは何か？

デュレーションは大きく分けて3つの考え方があると考える。

①　利回り価格曲線に引いた接線の傾き
　　　　⇒デュレーション
②　債券の平均回収期間
　　　　⇒マコーレデュレーション
③　債券の価格弾力性
　　　　⇒修正デュレーション

①一定の利回りの変化に対する債権の価格変動の大きさとしてのデュレーション

債券の理論価格は、将来得られるキャッシュを現在価値に割り引いて、それぞれを足し合わせることで求められる。

例えば、以下の条件の利付債券の場合を考える。

以上のような利付債は、1年後に2.0円、2年後に2.0円、3年後に2.0円、4年後に2.0円、5年後に102.0円（2.0円＋元本償還の100.0円）のキャッシュインが見込まれる。

満期5年の利付債は
残存期間1年　額面2.0円
残存期間2年　額面2.0円
残存期間3年　額面2.0円
残存期間4年　額面2.0円
残存期間5年　額面102.0円
の割引債のポートフォリオと捉えることができる。

従って、この債券の理論価格は、それぞれのキャッシュインを現在価値に割り引いて、合計すれば求められる。

以上より、この債券の理論価格は97.171円である。

ここから、一定の利回りの変化に対する債権の価格変動の大きさを測る方法として、デュレーションを求めることがある。

デュレーションの求め方は、利回り価格曲線の接線の傾きを求めることである。つまり、債券の理論価格の式を微分することで、その接線の傾きを求めることができる。

理論価格を微分したものがデュレーション

②債券の平均回収期間としてのデュレーション

債券の回収期間とは、例えば割引債であれば、残存期間＝回収期間といえる（利息の支払いがないため、キャッシュインは償還時のみだから）。

利付債の場合、以下の通り、（利息の支払いが年1回の場合）毎年キャッシュインが発生するため、残存期間＝回収期間とはならない。

上記利付債券の場合、キャッシュインの時点は５回あるが、そのキャッシュイン（回収）時点の平均はどこか、というのが「債券の平均回収期間」を表す。

利付債の平均回収期間を考えるときのイメージは下図の通り。

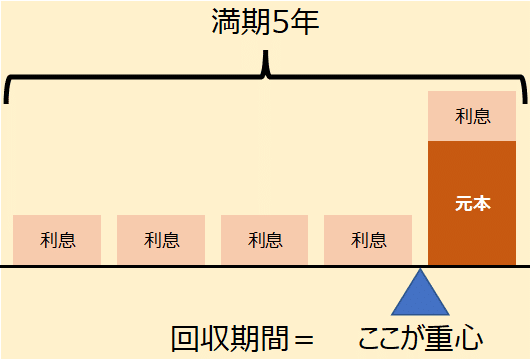
利付債の回収期間としてのデュレーション（＝マコーレデュレーション）は、償還までの期間よりも若干短くなる。

マコーレデュレーションは、利付債を割引債で組まれたポートフォリオと捉えたときに、それぞれのキャッシュインまでの各期間を各割引債の回収額のウェイトで加重平均した満期までの期間で表すことができる。

マコーレデュレーションを求める式は以下の通りとなる。

③債券の価格弾力性としてのデュレーション

金利の変化に対して、債券価格がどれだけ変化するか、を表したものが修正デュレーションである。例えば、修正デュレーションが2.96年のとき、金利が1％上昇したとき、債券価格は2.96％上昇することを表す。

修正デュレーションは、①のデュレーションを債券の理論価格で割り、符号を逆にしたもの（‐1をかける）として表すことができる。

マコーレデュレーション＝（1＋ｒ）×修正デュレーション
でもある。