
スプラトゥーン3の弾の命中率について #1 ブレの計算式
こんにちは。
スプラトゥーンの弾のブレには色んな仕様が絡んでいます。それらを理解すると最終的に各ブキの弾の命中率を計算することができます。最終的に「命中率を考慮したキル速の期待値」というものを求めることができたので、その報告をこの記事に書いていこうかと思っております。
この記事では、命中率計算に必要なパラメーターについて解説します。結果だけ見たい人は#3からの結果の記事を見てください。
スプラのインク弾のブレ
命中率の計算の前に、そもそも弾ブレはどんな仕様で計算されているのか、見ていこうと思います。そこで登場するのが、「拡散」と「ブレ値」という二つのパラメーターです。
なお、この#1の記事の内容に関しては、スプラの検証動画を作っているつーさんの動画を参考にさせていただきましたので、ここで引用という形にします。そちらも併せてご覧ください。
拡散
ご存知の通り、シューター、マニューバー、スピナー、ブラスターの弾はブレます。ZRを押して弾を撃った時、角度が横に少しズレるのです。

そのズレる角度のうち、理論上ズレる最大の角度が決まっています。これを拡散といいます。拡散が小さいほど弾が狙ったところに飛んでいきやすい、つまり精度がいいんですね。
例えば、スプラシューターの拡散は5° ですが、プロモデラーは13° です。
他の先駆者の方に倣い、この記事では拡散をs(単位は° )と表すことにしましょう。

拡散は以下の性質を持ちます。
・拡散の大きさはレティクルの横幅の大きさに反映される
例えば、レティクルが正方形(ブラスターの地上撃ちやシャープマーカーなど)なら拡散s=0° となり、拡散が大きいブキほど横に長い長方形のような形になります。
・ブキごとに地上撃ちの拡散とジャンプ撃ちの拡散が設定されている
例えば、スシとN-ZAPは地上撃ち拡散5°、ジャンプ撃ち拡散12° なのに対し、モデラ―は地上撃ち拡散13°、ジャンプ撃ち拡散16° です。
ジャンプ撃ちの拡散は「アクション強化」ギアで縮小させられますが、地上撃ちより拡散が小さくなることはありません。ZAPがエナスタを飲んでアク強3.9状態になっても、ジャンプ撃ち拡散は5° までしか下がりません。ちなみに、後述のブレ値がジャンプ撃ちでは大きくなってしまう(=初弾補正を受けられない)ので、たとえ拡散の値を地上撃ちと同じ値まで抑えても地上撃ちと同等の精度は得られません。
初弾補正及びブレ値の基本
しかし、実際に弾が0°〜sまで等確率でブレるかというと、そうではありません。実際は、撃ち始めはブレにくい、つまりレティクル真ん中(ズレ0°)に寄るようになっていて、撃ち続けるとブレやすく、つまり等確率に近づいていくのです。
これにはブレ値という戦闘中に上下するパラメーターが関わっています。ブレ値は通常$${b}$$で表され、小さいほど弾はブレにくく、大きいほど弾はブレやすくなります。なお$${0 < b \le 0.5}$$を満たしており、b=0.5だと完全に0°~s のランダムな角度に飛んでしまいます。

また、その$${0 < b \le 0.5}$$という範囲をさらに絞る形でブキごとに最小値と最大値があり、その範囲内で弾を撃つと増加し、撃たない間に減少します。また、ジャンプ撃ちをすると一気に大きくなります。具体的には、
・最小値(地上撃ちとジャンプ撃ちでも異なる)
・最大値(地上撃ちとジャンプ撃ちでも異なる)
・射撃一発あたりの増加量
・非射撃時、フレームあたりの減少量
などがブキごとに異なります。
よって、ブレ値bは次のような挙動を取ります。
①普段は最小値の値をとる
②撃ち始めると、一発ごとに一定の量ずつ増えていく
③撃ち続けると最大値で上昇が止まる
④撃つのをやめると、連射間隔分の時間を経た後一定の速度で減少していく
⑤最小値より下に下がることはない
これを図示したものが次のグラフになります。最小値、最大値、及び②の階段の段の高さと④の傾きがブキごとに異なります。(もちろん、連射間隔もブキごとに変わり、これは階段の段の横の長さに対応します。)

例えば、.96ガロンの場合、最小値=0.04, 最大値=0.3で、一発撃つごとに0.03増加し、非射撃時に1Fあたり0.02減少します。よって9発撃つとブレ値bが最大値を迎えますが、25F、つまり1/4秒弱でブレが最小値にまで減少します。一方、プライムは最小値=0.01, 最大値=0.25で、一発撃つごとに0.01増加し、非射撃時に1Fあたり0.005減少します。なので、24発撃たないとブレ値bが最大値まで到達しませんが、ひとたび最大までブレが増えると射撃をやめて最小値まで減少するまで56F(1秒弱)かかります。
ブレ値による弾のブレ確率の記述
ブレ値bにより、乱数ごとの射撃時のブレ角度の式が表されます。
$$
y = sx^{\log_{0.5}{b}} \;\;\;\; (0 \le x \le 1) \;\;\;\;\;\;\;\; (1)
$$
ズレる角度をy[°]、0〜1までの乱数をxとします。弾丸一発一発に対し逐一xが0~1の範囲でランダムに決められて、そのxによってズレる角度yが決定される、と考えてください。
ここで(1)式をグラフにすると、次のようになります。横軸がx、縦軸がyです。グラフはb=0.01の状態、つまりめっちゃブレにくい状態を表しています。このグラフを参考に(1)式を解釈してみましょう。
bによる補正なしでは$${y=sx}$$となり、xという0~1の乱数に従いブレ角度yも0°~sの乱数となるはずです。しかしブレ値bによる補正としてxが$${\log_{0.5}{b}(\ge 1)}$$乗されることにより小さくなり、結果としてyも小さく、すなわち射撃精度がよくなるのです。(補足:$${\log_{0.5}{b}}$$は、bが大きくなるにつれ小さくなる1以上の数、xは0~1の範囲の数のため$${x^{\log_{0.5}{b}}}$$は元のxより小さくなります。)
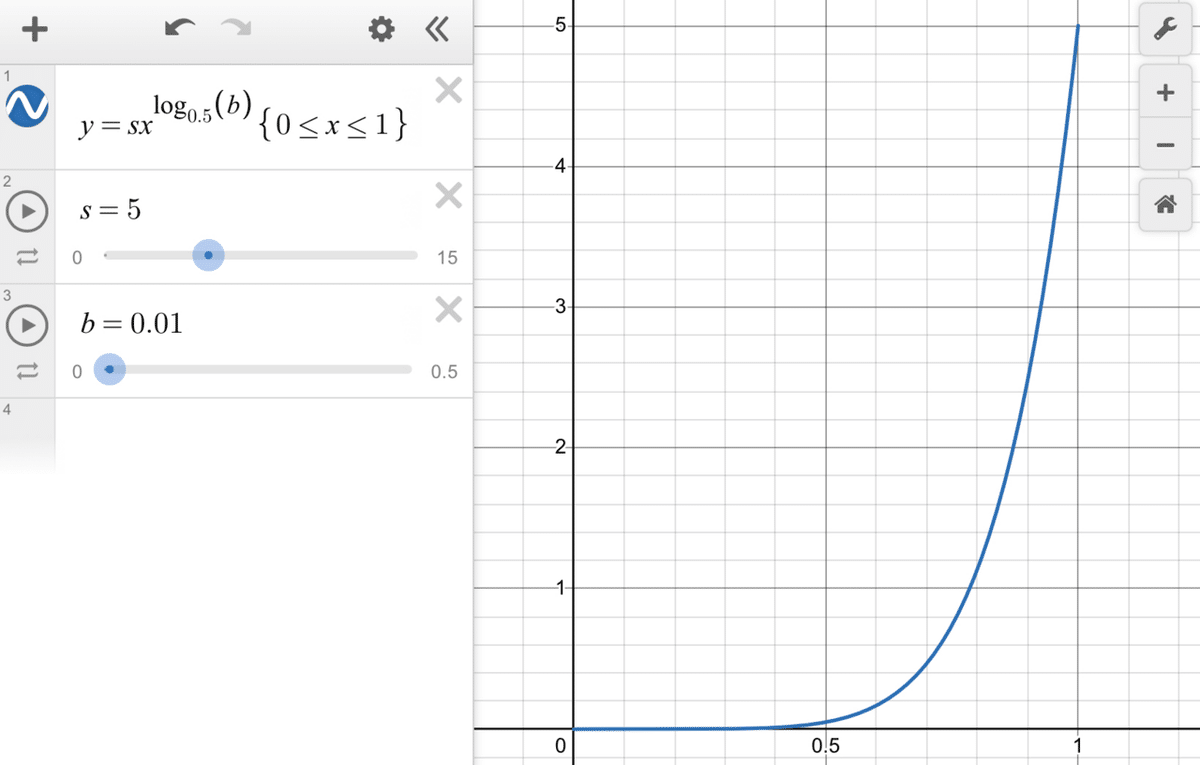
グラフに目を戻しましょう。現に、xが0.8より大きくなるくらいでないとブレが1°を超えません。つまり、b=0.01の条件下では8割くらいの確率でブレは1°以下に抑えられるのです。
命中率計算
ここで、(1)式を変形してx=〜の形にすると次のようになります。
$$
x = (y/s)^{\log_{b}{0.5}} \;\;\;\; (0 \le y \le s) \;\;\;\;\;\;\;\; (2)
$$
なんのために?と思うかもしれませんが、実はこのxは、弾のブレがy°以下に収まる確率を表します。(累積分布関数ってやつです。)
理由を述べておきましょう(読み飛ばしても後に支障はないと思います)。
乱数$${x}$$が例えば$${x_0}$$だったとするとブレ角度$${y}$$は$${sx_0 ^{\log_{0.5}{b}}}$$となります(この値を$${y_0}$$とおきましょう)。同様に考えれば、乱数xが0~$${x_0}$$の範囲であるとき弾のブレyは0~$${y_0}$$となっています。よって、乱数xが0~1の一様(等確率の)乱数であることを考えれば、$${x_0(=(y_0/s)^{\log_{b}{0.5}} )}$$の確率でyは0~$${y_0}$$の範囲内になります。
この(2)式は命中率の計算の際に活躍します。敵に当たる角度が求まれば当たる確率が求まりますからね。次の記事では、bの振る舞いを確認しつつ、実際に命中率計算をやっていこうと思います。
