
スプラトゥーン3の弾の命中率について #10 スピナー編~プログラム構築 その1~
#9でも述べましたが、今回の記事作成ではつーさんの弾道解説動画を参考にしました。計算の要となる基礎研究です。ありがたい… この記事の内容を議論するのに必要な基礎知識はだいたい動画内に述べられています。ぜひご覧ください。
スピナーの弾の仕様
スピナー特有の仕様:上下/初速ブレ
動画内でも触れられていますが、スピナーの弾は通常の左右ブレに加えて射角(=上下方向)のブレが発生し、さらに弾の撃ち出し初速も一定割合でランダムに増減するようになっています。
・左右ブレは他のブキとだいたい同じ。ただし初弾補正がなく、いつでも同じブレ方。なお、ほぼ全スピナーでb=0.3ですがクーゲルだけブレ値b=0.4です。長射程モードは拡散(そもそもの弾ブレ)が少ないから大丈夫だけど短射程モードはかなりブレます。
・上下ブレは、左右ブレと同じような計算式で導かれたブレ角度がもともとの射角に足される、といった形です。これにも初弾補正はなく、ほぼ全スピナーで$${b_上下=0.4}$$。クゲ長射だけ0.2であり、そのためクゲは長射は射程のブレが少ないです。
・初速は、これまた左右ブレと同じような計算式で割合増減します。やはり初弾補正はありません。どれくらいの割合増減するかはブキごとに違いますが、クゲ長射とイグザミナーがそれぞれ3%と5%、他が10%~15%程度といったところです。
よって、スピナーの弾は撃ってる間に性能が変化したりしません。撃ち続けるとブレが悪化するシューターとは対照的です。
ブレ角度/初速の計算式
以降、z軸を高さ(鉛直)方向、y軸を敵に向かう水平方向、x軸をそれに直交する水平の方向とします。つまり、敵との距離をdとすると敵の位置の足元は(0,d,0)です。
下図でいうと、赤線がx軸、敵に向かう緑線がy軸、上方向の青線がz軸になります。

z軸((x,y)=(0,0))から発射して敵((x,y)=(0,d))を狙います。
左右方向のブレ角度の大きさ$${|\theta_x|}$$, 上下ブレ角度の大きさ$${|\theta_z|}$$, 及び速度のランダム増減の量$${v_{増減量}}$$は次の式で表されます。(最初の式はこれまで何度も出てきましたね。)(x方向(水平方向)のブレはその値がそのままブレ角度になりますが、z方向(鉛直方向)のブレは元々の射角からの増分がランダム変化します。)ただし、$${x}$$は0~1で一様に変化する乱数です。
$$
|\theta_x|=sx^{\log_{0.5}{b}}
$$
$$
|\theta_z|=s_ax^{\log_{0.5}{b_a}}
$$
$$
v_{増減量}=v_0r_sx^{\log_{0.5}{b_v}}
$$
$${s_a,b_a}$$は上下方向の拡散とブレ値、$${v_0}$$はブレがなかった場合の初速、$${r_s,b_v}$$は初速の変化割合とブレ値です。これに、左右両方、上下両方、加速減速両方といった正負を考慮し、最終的に決定される左右方向の角度、上下方向の角度、初速の式は次の通りです。
$$
\theta_x=\mathrm{sgn}(2x-1)s|2x-1|^{\log_{0.5}{b}}
$$
$$
a=a_0+\mathrm{sgn}(2x-1)s_a|2x-1|^{\log_{0.5}{b_a}}
$$
$$
v=v_0(1+\mathrm{sgn}(2x-1)r_s|2x-1|^{\log_{0.5}{b_v}})
$$
何を言っているんだ?って感じかもしれませんが、要は左右も上下も初速も、ある程度(真ん中に)偏りながらブレるということです。
そのため、シューターやブラスターの時のように、上から見た図で弾が敵の当たり判定にぶつかったら当たる…なんて簡単な話ではありません。なぜなら、上下ブレと初速ブレの影響でレティクルを敵に合わせていても敵に届かない・飛び越してしまうといった現象が発生するからです。
ではどうするか。物理シミュレーションができたら良かったのですが、僕はその辺よく知らないので…pythonの数値計算でごり押しシミュレーションしました。(もっといい方法がある気はしますが…)弾道を計算して、敵の当たり判定にぶつかるかを判定、カウント…というのを繰り返して確率を求めれば命中率が求まりそうですね。
弾道の決まり方
弾道は、方向と初速が決まればあとは一定の法則に従って自動的に動きます。最初数F(スピナーはだいたい8F)は等速直線運動をし、その後計算式に従って減速し、減速終了後自由落下する、といった感じです。詳しい計算法はつーさんの動画内で解説されています。
この記事では弾道の計算の解説はしません。詳しくは、動画や公開されているdesmosファイルを見てください(丸投げ)。以降、初速と弾の上下方向の角度(射角)を決めれば、弾道を全部計算できるということにします。
弾道のデータ化
2次元(横から見た)弾道

図では点の間を線分で繋いだりしています。
スプラトゥーンの世界は現実ではなくデジタル世界なので、値は全て離散化(飛び飛びの値に)されています。時間も例外ではなく、弾道は結局0F,1F,2F,…目の弾の位置を逐次計算されてその通りに弾が飛ぶ、といった形になっています。
というわけで、発射した瞬間の点の座標と1F,2F,3F…後の点の座標、といった、弾の位置の座標たちでデータの列を作れます。

これは射角と初速によって決まるものだったので、初速の変化と上下方向のブレを考慮したものになっています。三次元上のシミュレーションをするために、これに左右方向のブレを考慮させた3次元座標のデータにしましょう。
3次元弾道
2次元の弾道に水平方向の角度をつけてやれば、3次元の弾道になります。具体的には、
・z座標(高さ方向)はそのまま
・x,y座標(水平方向)には、左右ブレ角度の方向に投射させる
つまりこうです。(2次元弾道をyz平面上に書いたうえで変換します。つまり、前章の配列が元の2次元座標空間でのy,z座標だと思ってください。)
$$
z_{3次元}=z_{2次元}
$$
$$
x_{3次元}=y_{2次元}\sin{\theta_x}
$$
$$
y_{3次元}=y_{2次元}\cos{\theta_x}
$$

上下ブレと初速ブレの影響を受けてランダムに動きます。

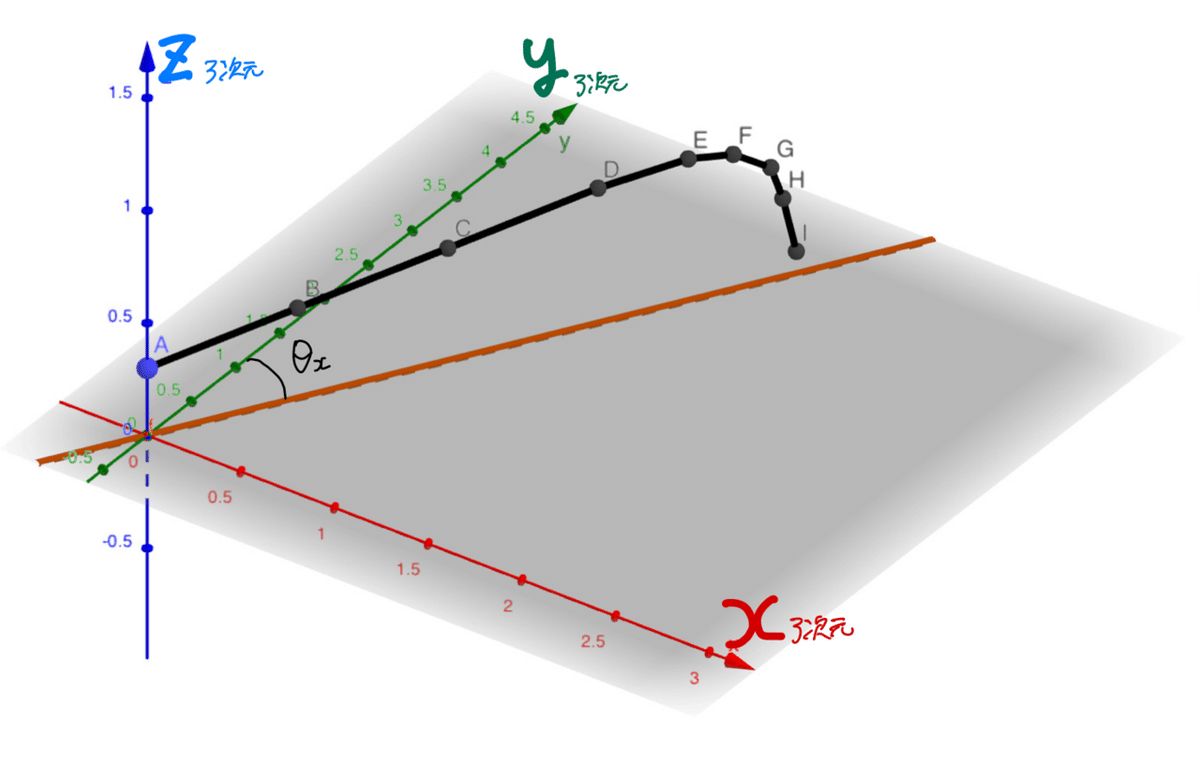
$${\theta_x}$$がランダムにブレます(=左右ブレ)
まあ要は水平方向の角度をつけてやった、ってことです。これで、弾道のデータを三次元空間内のデータとして表すことができました。

(x,y,z)の順番で、単位はDU
50DU=試し撃ちライン1本分(=5m) です。
衝突判定をするために
飛び飛びのデータをどう使う?~N弾道~
後はこの弾道が敵の当たり判定と重なるかどうかを判定したいのですが、上にある表のように弾道の値は飛び飛びの離散的な時間に対応する座標です。発射してからの時間を$${t[\mathrm{F}]}$$とすると、0F後にはこの座標、1F後にはこの座標、2F後には…といった感じです。そのため、ただ各時間において当たったか判定!としても、弾がN F目からN+1 F目の間(N:整数)に敵に当たる、というような状況で当たったと判定することができません。

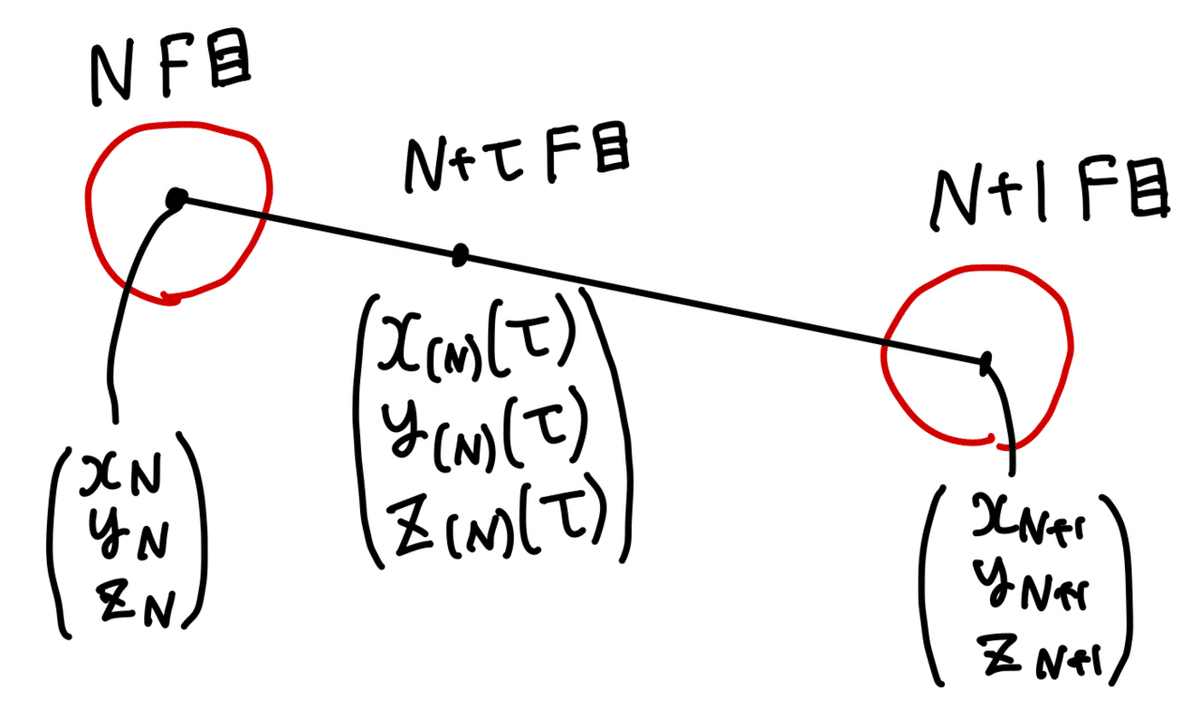
しかし、弾道は基本的にずっと等速直線運動はしませんが、N~N+1Fの過渡期においては等速直線運動すると考えてよいです。よって、下図のような線分上を1Fかけて弾は移動するということになります。
時刻N[F]における弾の位置を$${(x_N,y_N,z_N)}$$とし、
$${N\mathrm{F}< N+\tau < N+1\mathrm{F}}$$なる時刻$${N+\tau}$$(ただし、$${0 \le \tau <1}$$)における弾の座標を$${(x_{(N)}(\tau),y_{(N)}(\tau),z_{(N)}(\tau))}$$とします。その値は、
$$
\begin{pmatrix} x_{(N)}(\tau) \\ y_{(N)}(\tau) \\ z_{(N)}(\tau) \end{pmatrix} = \begin{pmatrix} x_N \\ y_N \\z_N \end{pmatrix} + \tau \begin{pmatrix} x_{N+1}-x_N \\ y_{N+1}-y_N \\ z_{N+1}-z_N \end{pmatrix}
$$
で求まりますね。線分のベクトル表示ってやつです。
よって、時刻$${t (\in \mathbb{R})}$$の弾の位置を求めるには、$${t=N+\tau}$$なる整数Nと0~1の実数$${\tau}$$を用いて$${(x_{(N)}(\tau),y_{(N)}(\tau),z_{(N)}(\tau))}$$を答えにすればいいですね。この時用いたN~N+1[F]での弾の弾道をN弾道ということにしましょう。
今後、弾が敵にぶつかる直前になったら、ぶつかる直前の時刻$${N(\in \mathbb{N}) [\mathrm{F}]}$$を求めてN~N+1FでのN弾道を求めて、本当にぶつかるかを判定すればいいですね。
敵イカの当たり判定
敵イカの当たり判定は…あまり詳しくは分かっていませんが、どうやら上から見ると円形で、身長は15DU(1.5m)弱らしいです。
参考ツイート:
こちらが立ち状態での当たり判定です🦑
— スプラッシュ3:スプラ3のレート対戦サービス (@splaaaash3) January 4, 2023
身体が描かれていない箇所も当たります⚡️
正面・横から見て楕円であることがわかります!
好評でしたらイカ状態の当たり判定も調査します! pic.twitter.com/N4Iogn7rqk
どうやら、頭の方の当たり判定が小さくなっているみたいです。今回は、それを反映(したつもり)して、わずかに身長の低い円柱として計算します。
横幅が3.6DUなので、縦を測ると、だいたい14DUくらいでしょうか?今回は13.7DUとして計算します。
今回の記事ではプログラム構築の準備をしました。次の記事では弾が敵に当たるかの判定プログラムを作り、またちょうどいい射角を関数として表現して命中率計算のための準備をします。
