
スプラトゥーン3の弾の命中率について #11 スピナー編~プログラム構築 その2~
衝突判定の詳細
命中の判定方法
さて、弾が当たったかどうかの判定をしましょう。あるブレ角度/初速を持った弾が敵に当たるか判定する関数を作りたいです。今回採った作戦はこうです。
①上から見た弾道が(上から見て)敵に当たっているかチェック。それで当たっていなければ当たるわけないので、外れている。当たっていれば続行。
②敵が射程外の場合、弾は外れる。射程内なら続行
③水平方向で弾が敵に重なったタイミングで弾の高さが敵の身長以内だったならば、当たる。(これは敵の当たり判定である円柱の側面に当たる場合を表す)
④ ③で当たらないと判定された場合、まだ曲射で上から当たる場合が残されている。弾の高さと身長が一致したタイミングで弾と敵の水平距離が敵の半径+弾の半径より小さいor弾の高さと身長+弾の高さが一致したタイミングで弾と敵の水平距離が敵の半径より小さければ、当たる。
⑤ ③④で当たらなかったら、外れている。
ちょっと厳密じゃない部分はあります(特に④は疑惑ですが…まあ……)が、まあ耐えでしょう。①~⑤の詳細を解説していきます。
①弾の軌道が敵に当たるような軌道か
①上から見た弾道が(上から見て)敵に当たっているかチェック。それで当たっていなければ当たるわけないので、外れている。当たっていれば続行。
射程距離と弾の高さは一旦無視して軌道上に敵がいるかだけを見ます。弾の高さがどんな値だろうとx,y座標から見て当たる方向ではない(上から見て飛ぶ方向が当たっていない)なら、当たるはずがありませんね。
その判定法は…今まで散々やってきたシューターの命中率の計算と同じです。左右にブレた角度$${\theta_x}$$が下図の角度より小さければ、軌道上に敵がいることになります。
$$
\frac{180}{\pi}\arcsin{\frac{r_t+r_b}{d}} \le \theta_x
$$

②敵が射程内か
②敵が射程外の場合、弾は外れる。射程内なら続行
弾の軌道は敵に当たる角度だが、届かないという場合を排除します。その場合、地面に着弾するときに
・弾が敵の外
・弾が敵より前
の2条件を達成していればいいですね。
「地面に着弾するときのx,y座標」を求めます。「N[F]目には着弾しておらず、N+1[F]目には着弾しているような整数N」を取り、N~N+1FのN弾道で$${z_{(N)}(T)=r_b \;\;}$$($${r_b}$$は弾の半径)を満たす時刻Tを求めれば、$${x_{(N)}(T),y_{(N)}(T)}$$が着弾時x,y座標となります。
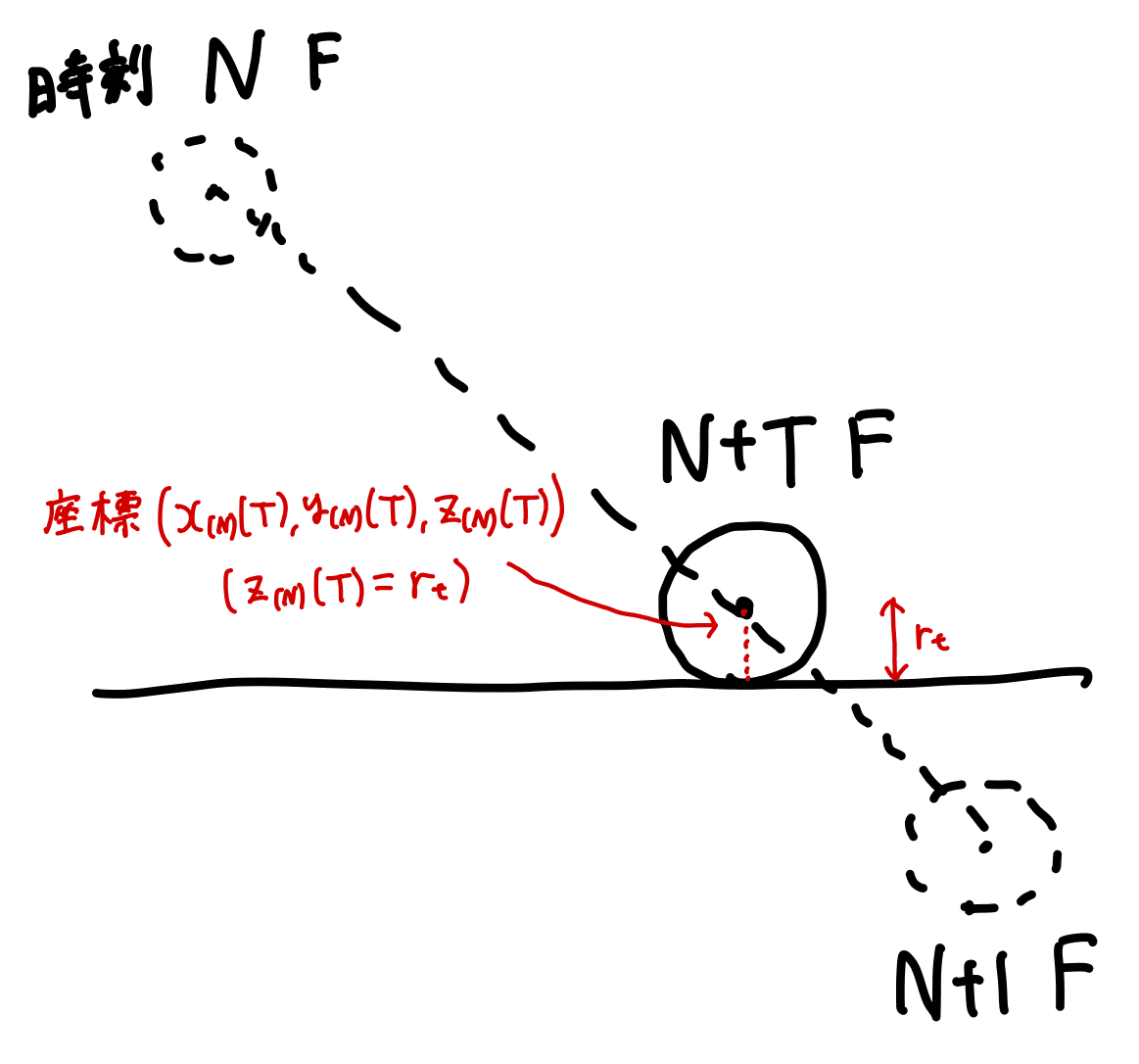
これら着弾時の座標を用いれば、上に挙げた2条件は
・$${x_{(N)}(T)^2+(y_{(N)}(T)-d)^2 > (r_t+r_b)^2}$$($${r_t}$$は敵の半径)
・$${y_{(N)}(T) < d}$$
と表されます。

③④ 当たったか判定
③④は、実際に当たるかの判定をようやく行っていきます。敵の当たり判定を円柱として計算するので、弾が当たるとは、当たる少し前の時刻を$${N (\in \mathbb{N})[\mathrm{F}]}$$とすると
$$
\left\{ \,
\begin{aligned} & x_{N}(T)^2+(y_{N}(T)-d)^2 \le (r_t+r_b)^2 \;\;\;\;(1式:水平位置) \\ &r_b < z_{N}(T) \le h+r_b \;\;\;\;(2式:鉛直位置) \end{aligned}
\right.
$$
を満たす$${0 < T <1}$$が存在することです。(円柱の端っこで厳密ではありませんが…まあだいたいこんな感じです。)しかし、実際は弾は位置がワープしたりせず連続に動きますので、円柱の外周部に弾が当たるかどうかを判定すればいいですね。よって、③側面に当たる場合として
$$
\left\{ \,
\begin{aligned} & x_{N}(T)^2+(y_{N}(T)-d)^2 = (r_t+r_b)^2 \;\;\;\;(1-3式:水平位置) \\ &r_b < z_{N}(T) \le h+r_b \;\;\;\;(2-3式:鉛直位置) \end{aligned}
\right.
$$
または④円柱の天井部分の円盤部分に当たる場合として
$$
\left\{ \,
\begin{aligned} & x_{N}(T)^2+(y_{N}(T)-d)^2 \le (r_t+r_b)^2 \;\;\;\;(1-4式:水平位置) \\ &z_{N}(T) = h+r_b \;\;\;\;(2-4式:鉛直位置) \end{aligned}
\right.
$$
なるTが存在しているかどうかを判定します。(なお、実際は④はもうちょっとだけ厳密に式を作ります。)
③水平方向で弾が敵と重なったタイミングで弾の高さが敵の身長以内だったならば、当たる。(これは敵の当たり判定である円柱の側面に当たる場合を表す。)
まず当たる直前の時刻$${N (\in \mathbb{N})[\mathrm{F}]}$$を求めます。とりあえずNを適当な小さい数字にして、敵との水平距離が大きく当たっていない、かつy座標が小さくまだ未到達である間はNを1ずつ大きくしましょう。そうすれば、当たる直前でNが止まります。
そうしたら、時刻NにおけるN弾道を計算し、それを用いて「水平方向で弾が敵と重なったタイミング」のT(つまり、1-3式を満たすT)を求めます。
$$
\begin{aligned} &x_{N}(T)^2+(y_{N}(T)-d)^2 = (r_t+r_b)^2 \\
&\Leftrightarrow \{(x_{N+1}-x_N)T+x_N \}^2+\{(y_{N+1}-y_N)T+y_N-d\}^2=(r_t+r_b)^2 \\
&\Leftrightarrow \alpha T^2+2\beta T+\gamma=0\\
&\Leftrightarrow T=\frac{-\beta \pm \sqrt{\beta^2-\alpha\gamma}}{\alpha}
\end{aligned}
$$
と計算でき、Tを求められます。ただし、α,β,γは係数で、次の通りです。
$$
\begin{aligned} \\\alpha&=(x_{N+1}-x_N)^2+(y_{N+1}-y_N)^2,\\\beta&=x_N(x_{N+1}-x_N)+(y_N-d)(y_{N+1}-y_N),\\\gamma&=x_N^2+(y_N-d)^2-(r_t+r+b)^2 \end{aligned}
$$
そうしたら、その時の高さが円柱に当たるような高さかを判定します。つまり、2-3式である
$$
r_b < z_{N}(T) \le h+r_b
$$
が成り立つかチェックします。成り立っていれば、円柱の側面に弾がヒットしたことになります。
④ ③で当たらないと判定された場合、まだ曲射で上から当たる場合が残されている。弾の高さと身長が一致したタイミングで弾と敵の水平距離が敵の半径+弾の半径より小さいor弾の高さと身長+弾の高さが一致したタイミングで弾と敵の水平距離が敵の半径より小さければ、当たる。
と言われても、何のことやら…という感じだとは思いますので、解説します。
③が円柱の側面に当たる場合だったので、④では円柱の天井部分の円盤(以下、円盤)に当たる場合を考えればいいですね。つまり、④は曲射で頭の上から当たる場合に対応します。
本来は、「円柱の各点~弾の位置の距離の最小値が弾の半径以下」であれば当たると言うべきなのですが、それを計算するのは面倒なので(計算量少な目でpythonで実装できる案があったら、どうかコメントよろしくお願いします(丸投げ))
・とりあえず、円盤と弾の高さが同じタイミングで弾の位置が近ければ当たっている。
・上記の判定で取りこぼした、円盤の上でかすって円盤から離れていく弾道の場合を拾う。
という判定法で行きます。
円盤と弾の高さが同じタイミング、(下図)つまり
$$
\begin{aligned} &z_N(T)=h \\
&\Leftrightarrow z_N+T(z_{N+1}-z_N)=h\\
&\Leftrightarrow T=\frac{h-z_N}{z_{N+1}-z_N}\\
\end{aligned}
$$
が成り立っているときに、$${r_t+r_b}$$より弾と敵の距離が近ければ($${x_{N}(T)^2+(y_{N}(T)-d)^2 \le (r_t+r_b)^2}$$)当たりそうですね。

しかしそれでは次の場合を包摂できません:敵の頭をかすめて当たり、弾の高さが円盤の高さと合う頃には弾は遠くに行ってしまっているパターンです。(下図)

にもかかわらず、弾は当たっている
そのために、頭をかする場合(下図)を判定します。つまり、かするような高さ=弾の位置イコール円盤の高さ+弾の半径 にて、弾が円盤半径の内部にいる場合です。

式にするとこうです。
$$
\begin{aligned} &z_N(T)=h+r_b \\
&\Leftrightarrow z_N+T(z_{N+1}-z_N)=h+r_b\\
&\Leftrightarrow T=\frac{h+r_b-z_N}{z_{N+1}-z_N}\\
\end{aligned}
$$
なるTが、$${x_{N}(T)^2+(y_{N}(T)-d)^2 \le r_t^2}$$を満たしている場合です。Tの値を代入して判定すればいいですね。
この計算で使うNの値は、N[F]目の弾が円盤より高く、N+1[F]目の弾が円盤より低いような$${N(\in \mathbb{N})}$$を用いればいいです。pythonでそれを計算するなら、$${z_{N+1} < h < z_N}$$が成立していない間、弾が低ければNを小さく、弾が高ければNを大きくしていけばいいでしょう。
これら③④の判定を行い、いずれでも当たっていないとの結果を得たなら、外れていると判定します(⑤)。これで衝突判定は終了です。お疲れさまでした。
命中率計算に使う射角の値
弾道を用意すれば弾が敵に当たるかの判定ができるということなら、それをシミュレーションしまくれば命中率が求まりそうです…が、一つ問題が発生します。射角をいくつにするのか?という問題です。スピナーは上下方向も考えなければならないので、射角によって命中率が変動します。ブキの性能比較として命中率を求めるなら、最も命中率の高い射角で測りたいですよね。
というわけで、敵の距離に対して最適な角度を求めましょう。角度と初速のブレなしの場合に敵のど真ん中に当たるような弾道になる角度を最適な角度と呼ぶことにします。弾は最初数フレームは直進しそのあと落ちます。直進している間に当たる場合は簡単な計算で求まりそうです。
・直進中に当たるような近い距離の場合
弾の出る位置は、おおよそ高さ4.5DUです。そこから弾が出て敵の身長hの半分の高さに当たるような角度は、下図のaです。d1は弾が直進できる限界の距離とすれば、0<d<d1での最適角度optangleは次の式の通りです。
$$
\mathrm{optangle}(d)= a(d)=\frac{180}{\pi}\arctan{\frac{h/2-4.5}{d}} \;\;\;\;(0< d \le d_1)
$$

敵のど真ん中の座標は(0,d,h/2)
・落下中に当たるような遠い距離の場合
落下の弾道は各時刻において逐次計算していくもので、距離の関数で表せるようなものではありません。よって、統一的な式で最適角度を求めるのは…多分無理です。
しょうがないので、適当な関数で最適角度を表し、それがだいたいどの距離でも敵のど真ん中に当たるように関数を微調節します。適当な関数は…なんか$${d=d_1}$$のときのaから最終的に10°くらいまで大きくなる関数を設定して係数や冪乗の数を調節します。
最終的に、こうなりました。d2は、ブレなしでの射程限界です。このα1,α2,α3が、ブキごとに微調整する数字です。(とはいえ、大体似通っています。α1≒8°、α2,α3≒3でα3がα2よりわずかに大きい程度です。)
$$
\mathrm{optangle}(d)=a(d_1)+\frac{(\alpha_1-a(d_1))(d-d_1)^{\alpha_2}}{(d_2-d_1)^{\alpha_3}} \;\;\;\;(d_1 < d)
$$

なお、角度が大きくなるとあまり射程が変わらなくなるため15°で打ち切りにしている
この最適角度を使って敵に命中する高さを求めると、次のグラフのようになります。

敵の身長h=13.7としてある
射程限界前まではだいたいh/2で安定し、射程限界近くでガクっと下がる形にちゃんとなっていると思います。この射角を使えば命中率を正しく求められますね。
これでスピナーの命中率を計算する準備が整いました。結果は…#9で見せたのがだいたいそうなのですが、気が向いたら詳しい考察をしようと思います。
