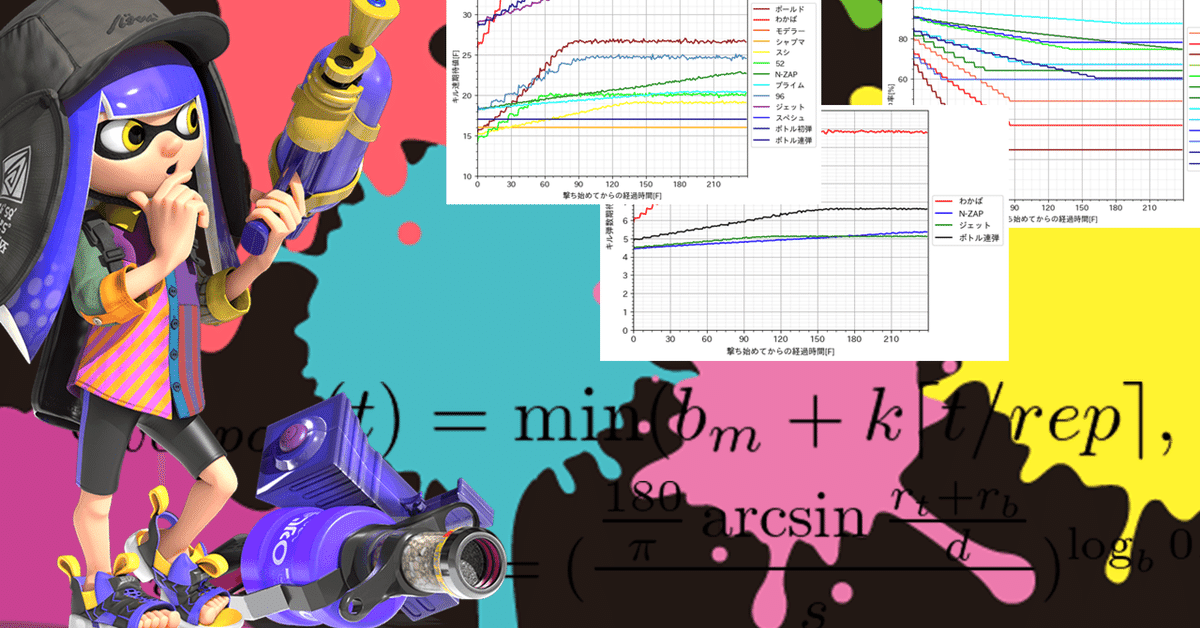
スプラトゥーン3の弾の命中率について #4 キル速の期待値
※6/24追記
7.2.0のアプデでのスペシュの上方を忘れていました。修正しておきました。
何発で倒せる?
必要弾数の期待値
命中率を計算できれば、敵をキルするために撃たなければならない弾の数の期待値(平均)も求めることができます。例えば、スシは理論上は3発でキルできますが、実際は10数%の確率で一発外してしまいますし、そうなるとブレが悪化してさらに上がった外す確率を引いてしまうかもしれません。というわけで、スシがキルをするまでに撃つことになる弾数の平均を求めることができますね。
とはいえその期待値を直接計算するのはなかなかにしんどいですね。スシの場合、3発でキルできる確率は1発目~3発目の命中率を掛け合わせればいいですが、4発かかる場合、1発目~3発目どれを外すかで場合分けが生じ、さらにそれら全て確率が異なります。5発の場合、1発目~4発目の内どの2発を外すかでさらに場合分けが生じ…少々面倒ですね。
ひとまずここは、pythonによるシミュレーションに頼りましょう。キルまでにかかる弾数を計測する作業を10000回ほど繰り返し平均を取りました。
各ブキのグラフ
確定数で分類して見ていきましょう。なお、例によって全部射程端での値です。

ガロン系統は2確ですが、そこそこの確率で3発撃たなければならないみたいです。52なんか、撃ち続けると3発かかる方が普通という…初弾補正を活かすことの重要性が分かりますね。

3確シューターです。プライムが思ったより強いですね。スシは撃ち続けると、ほぼ実質4確になってしまうと言っても過言ではありません。ボールドは、撃ち続けると悲惨ですが、初弾からならまあ1発外すくらいで済むことが多いみたいです。

4確シューターも、射程端で撃ち続けるとほぼ5確みたいになっちゃいますね。わかばなんかは、接射が前提になってくるのでしょうか?

モデラ―はもう射程端で戦うことは想定されてません。スペシュも大概ですが、実はスペシュは最初から精度が悪く、そのあと同じくらいの低精度を維持しているんですね。スプラ公式twitterの説明文にあった、「撃ち続けてもあまりブレが大きくならない特徴があるぞ」って、そういう…
キル速の期待値
前節で求めた「必要弾数の期待値」を使えば、「キル速の期待値」だって求められそうですね。
というわけで求めました。計算式は、スプラ3wikiでも採用されている
$$
{(キル速[\mathrm{F}])=1 \mathrm{F} +((必要弾数)-1)*(連射間隔[\mathrm{F}])}
$$
を採用しました。なお、ボトル初弾に関してはどうしても連打速度にムラができてしまうため、相当な熟練者でないかぎり1~数フレームキルが遅れそうです。

キル速が早いブキでも、ブレによりキル速の期待値は低減してしまいます。こう見ると、各ブキのブレも含めたキル力がよく表せてる気がします。対面をどう戦うかの参考になりそうですね。

短射程:赤系
中射程:オレンジ~緑系
長射程:青系 としている。
グラフにもしてみました。カタログスペック上ではわかばとシャプマのキル速は同じですが、期待値という観点で見ると全然違いますね。同様に、スペシュとジェットもキル速の理論値は一緒です。

拡大しました。撃ち始めはやはり52が強く、スシ、ボールドと続きます。ですが0.5秒も戦闘が続くとシャプマの安定性が光ります。また、思ったよりN-ZAPが頼りなく、8.0.0のアプデもやむなし…だったのかも?スシは、シャプマボトルの安定性には負けますが、自慢のブレ補正により粘り強いです。
また、プライムの「決して弱くはないんだけどボトルが…」感はこのグラフから読み取れそうです。ボトルは熟練者でなければもう1~4F程度遅れて線が上にズレそうですが。結局、ボトルが誤差1F程度の「ほぼ最速連打」をできなければ、ボトルは初弾からの勝負においてプライムでも有利が取れる程度ですし、逆にボトルが最速連打してきて、さらに長期戦になったら下手な中距離シューターより強いということです。

中距離シューターの主戦場であろう射程距離2.0ライン分で撃った場合のグラフです。ある程度カタログスペックを発揮できるようになってくれてるみたいですが、この距離でもガロン系統のブレは時間が経つほどきつくなっていきます。ジェットは近すぎて命中率100%になっていますが、それでもキル速では勝てないことが見て取れますね。
アプデによる向上(ボールド、スシ、N-ZAP、スペシュ)

ボールドは7.2.0のアプデで弾の多さが拡大しました。これにより、近距離、射程端ともに1F程度のキル速期待値向上がなされたことになります。
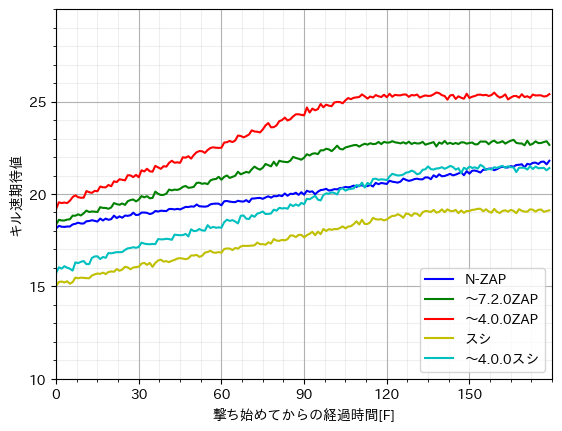
スシ、ZAPは4.1.0で拡散が6°→5°になり、ZAPはさらに8.0.0でブレ増加量が半分になりました。どちらにせよ一回のアプデで、撃ち始めは1F弱、撃ち終わりでは2F程度キル速期待値が短縮されたことになります。
アプデで命中率が向上した、といっても実感が沸かないかもしれませんが、キル速にして1F程度の向上と考えるとなかなか絶妙な調整だと思いませんか?

スペシュは7.2.0のアプデで拡散が6°→5.5°になりました。それにより、キル速にして2F程度の向上が見込めます。
こんな感じで、命中率を考慮したキル速という概念について考察してみました。この「キル速の期待値」により、いわゆる「ブキの対面の強さ」がちょっと定量化できたと思います。対面の際の参考にしてもらえると嬉しいです。
おまけ:必要弾数の理論計算
前章にて、直接計算するのはしんどいと言いましたが、不可能じゃないです。理論計算していきましょう。
$${p_i}$$をi発目の命中率(前回の記事の内容から計算できるので、これは既知です)、$${P(i,n)}$$をi回中n回命中させる確率とします。「i回目の射撃でn発目の命中弾を当ててキルする」確率(n確のブキでi回の射撃でキルする確率)は「i-1回目までにn-1発当てており、かつi回目に弾を当てる」確率であり、式で表すと$${p_i P(i-1,n-1)}$$です。このとき、かかった弾数がiなので、このiに先ほどの確率をかけて全iに関しての総和を取ればキルするのにかかる弾数の期待値が求まります。つまりこうです。
$$
E(キル)=\sum_{i=n}^{\infty} ip_iP(i-1,n-1)
$$
あとはP(i,n)が求まればokです。なお、上式ではiを∞まで飛ばしていますが、現実的にさすがに当てられるであろう弾数、せいぜいi=25程度で十分と思われます。(ただし、モデラ―とかいう武器は25発あってもキルできないことが普通にあるので極端にブレやすいやつらは例外です。)
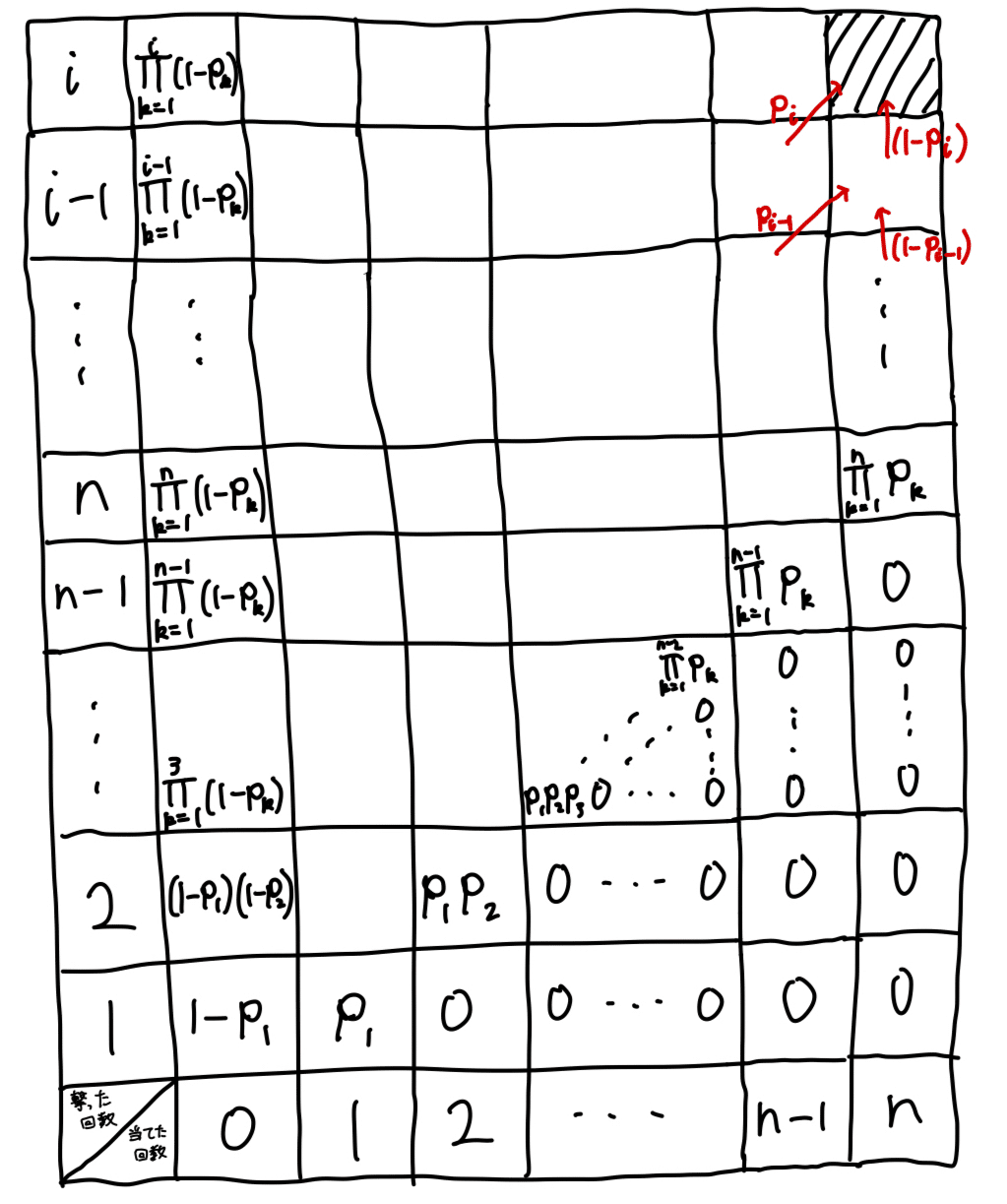
では、P(i,n)なのですが、漸化式が立てられますね。i回中n回命中するのは、i回目が当たるか当たらないかで場合分けが生じます。弾が当たるのを○、当たらないのを×とすると、下図のようになります。

図の説明から、
$$
P(i,n)=p_iP(i-1,n-1)+(1-p_i)P(i-1,n)
$$
これを解けばよいでしょう。それは、P(i,n)を表す下表を埋めることに対応します。
i回当たって全弾外す(表の最左列に対応します)確率は、1発目~i発目が外れる確率の総積なので、$${\prod_{k=1}^{i}(1-p_k)}$$です。また、i<nは起こりえないので確率は0で、1回中1発当たるのは当然$${p_1}$$で、i回中i回当たるのは$${\prod_{k=1}^{i}p_k}$$です。この初期条件の下で表を埋めさせるような関数をpythonで組んであげれば正確なP(i,n)が、伴って必要弾数も求まります。
さて、計算の結果なのですが、下表にようになります。

モデラーの結果がおかしいですが、その他にはそう大きな欠陥は見当たりません。モデラ―の異常は、i=25までしか足していないことに起因しています。ブレ最大のモデラ―は25発撃ってもキルできないこともザラなのに、26発以上撃った際の必要弾数を計上していないから値が小さく出てしまうんですね。

いろいろやってきましたが、結局この、前章でやったようなシミュレーションの方が手っ取り早く正確だと思います。以上、おまけでした。
