量子ゲートコンピュータを用いた機械学習アルゴリズムQCLと化学分野での利用検討の記事(の下書き)
本記事の目的
昨年に報告した「量子回路学習(quantum circuit learning, QCL)のアルゴリズムを化学分野で適用してみた論文」について、背景となる理論を含めて日本語で解説した記事です。
某案件で解説文書の執筆を頼まれたので、下書きを兼ねて、内容を公開します(referenceなどはあまり入れてません)。
注: 経緯があってこの研究をしていますが、実のところ、筆者のメインの専門は量子コンピュータではありません。内容に誤りを見つけたら、ご指摘いただけると助かります。
元となる原著論文はこちら
はじめに
量子ゲートコンピュータは一つの新たなコンピューティングのパラダイムとして期待されている。現時点において、通常の古典型コンピュータの性能を上回る事例は少ないが、将来的には計算システムの変革も予感される。本記事では、量子コンピューティングのアルゴリズムの一つである量子回路学習(QCL)の基礎となる考え方や、ケモインフォマティクスという化学の一分野での利用事例について説明する。
1. 量子ゲートコンピュータの概要
量子ゲートコンピュータの特徴と数学的な取り扱いについて、必要最小限の解説を、専門外の方向けに行う。詳細や周辺情報等については、量子分野の専門家による書籍などを参照されたい。
Webサイト(抽象理論を理解できる大学生以上向け)
バイブルとされる書籍(専門向け)
機械学習関連も含めた書籍(専門向け)
1.1 量子ゲートコンピュータの基礎概念
量子ゲートコンピュータとは、量子ビット(qubit)を基本要素として計算を行うコンピュータの一形態である。これは古典的なビットとは異なり、0と1の状態を同時に取ることができる、量子重ね合わせの性質を持つ。また、量子ゲートコンピュータは操作や計算の過程で、複数の量子ビット間での相互作用を用いることが多い。この相互作用の中で、特に注目されるのが「重ね合わせ」と「量子もつれ」という現象である。
重ね合わせは、一つの量子ビットが同時に複数の計算状態を保持することができる性質を指す。具体的には、0と1の両方の状態の情報を一度に処理することが可能であり、これにより古典的なコンピュータよりも高速な計算が期待される。この原理を生かした、量子アニーラとよばれるハードウェアが注目されている。アニーラは量子コンピュータを組み合わせ最適化問題の求解に特化させたハードウェアであり、材料科学を含めた様々なタスクで、古典的なマシンに対する優位性が示されつつある。
量子もつれとは、二つ以上の量子ビットが互いの状態と強く関連づけられ、一方の状態が変わると他方の状態も即座に変わる現象を指す。この量子もつれは、量子情報処理や量子通信などの分野での応用が研究されている。もつれた量子ビットは、距離が離れていても互いの状態に影響を与えるため、例えば量子暗号や量子通信の実現において重要な役割を果たすとされる。
量子もつれや重ね合わせが関わる相互作用は極めて複雑である。古典コンピュータによって本現象をシミュレーションするための計算コストは量子ビットに対して指数関数的に増加することが示されている。2023年時点においては、専用のスパコンであっても40量子ビット程度のシミュレーションが限界である(ref)。一方で、真性の量子コンピュータは、本計算を自然現象に基づいて瞬時に行うことが可能である。このような着想に基づき、古典マシンでは計算が困難な課題を、高速計算機としての自然に代行させるのが、量子コンピュータの基本思想である*。
*23年3月に理化学研究所に導入された量子コンピュータは64ビットである(ref)。現在のシステムには計算ノイズ等の問題があるものの、今後も指数関数的な計算能力の向上が期待されているので、量子マシンへの世間的な注目が集まっている。
1.2 量子ゲートコンピュータの簡単な理論
本項では、量子回路学習の実装に必要な最小限の理論を説明する。
1.2.1 1量子ビット系
はじめに、1量子ビット系の状態表現について説明する。通常のコンピュータのビットは0または1の2状態しか存在しない。それに対し、量子ビットは2変数分の自由度を取ることができる。量子状態を回転角θ、φによって表現し、人間用に可視化したのが「ブロッホ球」である。ある量子状態は、球の中の矢印の向きとして表現できる*。
*ただし後述の量子もつれが存在する場合は、ブロッホ球による表現はできなくなる。

1量子ビット(これを|ψ>とする)に対する数学的表現は以下のようになる*。

*残念ながら、量子力学は複素空間上での事象のため、状態表現には、複素数を導入する必要がある。後述の通り、直感的なユークリッド座標系とは異なる挙動を取る場合もしばしばある。「そういうものである」と「納得」するしかない。
ここで、(1, 0)^T、(0,1)^Tは基底ベクトルであり、ユークリッド座標系におけるx,y,z単位ベクトルに対応する。
両ベクトルはそれぞれ、|0>、|1>と表記されることが多い。

ここで、|0>は基底状態と呼ばれる。
1.2.2 量子ゲート
量子ゲートコンピューティングとは、基底状態(|0>)の量子ビットに対して、種々の演算処理を行い(矢印の向きを変え)、最後に矢印がどこを向いているかを観測する作業である。

量子演算はゲートと呼ばれる操作によっておこなわれる。量子ゲートには様々な種類が存在するが、基本的な3つのゲートセットを組み合わせれば、任意の演算を行うことが可能である(ユニバーサルゲートセット)。これは、古典コンピュータ上の任意の演算がNOT・ANDゲートの組み合わせで行えるのと類似の話である。
ゲートセットには様々な選び方があるが、本項ではRx, Ry, CNOTの組み合わせを扱う。Rx, Ryは、図に記載の通り、矢印の向きをxまたはy軸方向に回転させるゲートである(CNOTは後述)。
Rx,Ryゲートの行列表現は、以下のとおりである(tは回転角)。
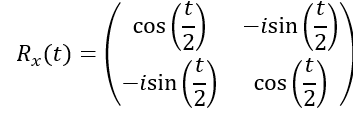

ユークリッド座標系での回転行列と類似しているが、複素空間での処理のため、Rxの行列中には複素数が入っている。
例えば、計算開始時点の基底状態|0>の量子ビットにRx(s)、Ry(t)の回転ゲートを順に適用する操作は、次の行列演算で表現できる*。
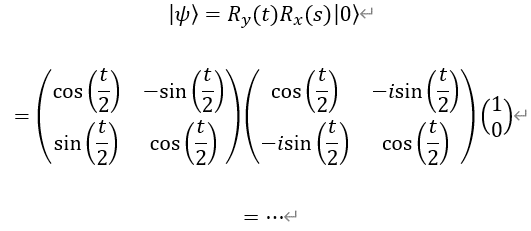
*ユークリッド系ではx,y軸の順で回転しても、y,x軸の順で行っても、同じ結果が得られる。しかし複素系ではこれが成立せず、Rx(s)Ry(t) ≠ Ry(t)Rx(s)となる。直感とは異なる結果であり、注意が必要。
1.2.3 観測
量子コンピュータでは計算結果を得るために、量子状態の観測処理を行う。しかし実際の量子コンピュータでは、ブロッホ球の矢印そのものを観測することはできない。可能なのは、z(またはx,y)軸方向に対して、矢印が順向き(+1)または逆向き(-1)であるかを観測することのみである。
z軸に対して観測値が順・逆向きのどちらかになるかは量子力学の確率論で決まる。そこで複数回のサンプリングを行うえば、z軸方向に対する期待値(-1~+1)が得られる。これが、一般に言う量子コンピュータの演算結果とみなされる*。
*φ方向の位相についても、位相推定と呼ばれる量子アルゴリズム・回路を用いることで、期待値を取得できる。
1.3 多量子ビット系
量子コンピュータの本領は、複数のビットが複雑に相互作用する多量子ビット系で発揮される。各量子ビットがそれぞれ相互作用を行うため、Nビット系では、システム全体の記述に2^Nの情報量が必要になることを示す。
1.3.1 テンソル積
はじめに、2量子ビットの状態を記述する方法を考える。多ビット系の状態や演算行列は、テンソル積⊗と呼ばれる計算を使って表現することになる*。
*数学から遠い分野の人間にとって、テンソル積⊗は気味の悪い記号に映るかもしれないが、そこまで難しい演算子ではない。
例えば、2つの量子ビットが基底状態|0>にあるとき、系全体は以下のように記述される。

同様に、片方または双方が|1>である時は、以下の表現になる。

ブロッホ球の対応は以下のようになる。

ここで、系全体を記述するのに必要なベクトルが2から2^2 = 4に増えた点に注意されたい。これを一般化すると、N量子ビット系では2^N次元のベクトルが必要になる。
多ビット系のゲート演算も、同様にテンソル積で定義される。例えば、1つ目のビットのみにRyゲートを作用させるのであれば、二次元の単位行列Iを用いて、Ry⊗Iを計算し、2^2 x 2^2行列を得れば良い。
1.3.2 CNOTゲート
本稿で登場する最後の演算はCNOTゲートである。CNOTは2量子ビット間の相互作用を誘起する。また、Rx, Ry, CNOTは3つあわせてユニバーサルゲートセットと呼ばれ、これらの組み合わせで、任意の量子回路を構成できる。
例えば第1、2量子ビット間にCNOTを作用させる演算行列は次のように表現できる。

ブロッホ球でCNOTの役割を表すと以下のようになる。

第一ビットが基底状態|0>の時は何もせず、|1>の時は第二量子ビットの符号を反転するという役割がある。
一方で既に述べたように、一般の量子ビットの状態は|ψ>は|0>と、|1>の重ね合わせである。

「|0>と|1>の重ね合わせ状態の量子ビット」に対して、「|0>の時は何もせず、|1>の時は他の(重ね合わせ状態にある)量子ビットの符号を反転する」という、直感的には理解の行き届かない演算処理を経ることで、量子もつれ状態が生成する。
CNOT演算後の量子状態は複雑であり、もはやN個のブロッホ球で表現することはできなくなる(i.e., 2^N個の状態を考える必要がある)*。
*この複雑な状態をうまく使いこなそうとする試みが、量子コンピューティング研究である。
2. 量子回路学習(QCL)
2.1 QCLに至る背景
量子技術の用途として、量子化学計算、秘密通信、機械学習などが知られる。量子回路学習(quantum circuit learning, QCL)は量子ゲートコンピュータのアルゴリズムの一つで、御手洗らによって提案されたものである(Phys. Rev. A 2018)。
現在の量子ゲートコンピュータは、ビット数の制限や計算ノイズの問題などがあり、演算能力に制約がある。特に、ノイズによってどうしても生まれてしまう演算上のミスを修正する「誤り訂正機能」を実装するのが困難な状況にある*。
*このような、誤り訂正機能を持たない中規模の量子ゲートコンピュータをNISQ (Noisy Intermediate-Scale Quantum Computer)と呼ぶ。2023年時点においては、NISQをいかに使いこなすかを念頭に置いた研究が多い。
こうした背景もあり、全ての処理を量子コンピュータで行うのではなく、補助的に古典コンピュータを併用する量子・古典ハイブリッドアルゴリズムが提唱されている。QCLもこの範疇に含まれる。
2.2 QCLの基本動作
一般に、教師有り機械学習の挙動は、y=f(x,θ)と記述することができる。ここでyは目的変数、xは説明変数、θは学習パラメータ、fは予測アルゴリズムである*。
*例えば単純な一次回帰y=ax+bであれば、θ=(a,b)となる。
QCLは教師有り機械学習アルゴリズムの一種であり、機械学習の推論処理のみを量子回路で実装する仕様になっている(下図)。予測誤差の計算やθの微調整は、全て古典コンピュータによって行われる。

教師有り機械学習のアルゴリズムとして、古典コンピュータにおいても様々な種類が提案されている(線形回帰、ニューラルネットワーク、サポートベクタマシン、決定木、…)。そのような多くの選択肢がある中で、敢えて予測関数として量子回路のアルゴリズムを選択する理由は、実は自明ではない。しかし後述のように、一部タスクでは既存手法を上回る性能が観測される場合もあった。QCLの意義については次項で考察する。
2.3 QCLの回路構成
QCLを構成するための回路設計に制約はなく、自由に演算子を選んでよい。ここでは例として、Rx,Ry,CNOTゲートによって2量子ビット系の簡単な量子回路を考える。

回路の挙動は次のとおりである。
(1) 量子演算は基底状態|0>からスタートする。
(2) 各量子ビットに、Rx,Ryゲートをそれぞれ作用させる*。このときの回転角として、xに対応するベクトルを反映させる。
(3) CNOTゲートを作用させ、量子もつれ状態を誘起させ、回路に複雑さと表現力がもたらされる
(4) 学習パラメータとしてθに対応するゲートを作用させる*。
(5) 第一量子ビットのz軸方向の状態を観測してyの期待値を得る。
*「任意の回転はRx, Ry, Rxゲートの積で記述できる」という定理が存在する。そのため、フルスペックでは3つのゲートを作用させた方が良いが、本例では簡素な理論式を得るため、ゲート数を減らした。
回転ゲートRx, Ryによって、連続値としてのパラメータx =(x1, x2), θを回路内に反映させている点が、QCLの一つのポイントである。
このような単純な回路構成であっても、解析解はかなり複雑になる(図右)。量子ビットやゲート数を更に増やすと指数関数的に式が複雑になり、解析解の計算やシミュレータでの数値計算が困難になる。このような指数関数性と、通常の古典アルゴリズムではあまり見かけないsin, cosの組み合わせからなる理論式が、QCLの機械学習モデルとしての特質と言える。
論文で用いた量子回路の構成を以下に示す。

N量子ビットに対し、それぞれRx, Ryゲートを入力xに対して作用させる。次に、隣り合うビットごとにCNOTゲートを設定し、量子もつれを誘起する。更にθを入力とする回転ゲートRx, Ry, Rxを作用させ、回路に学習パラメータの情報を埋め込んだ。後者の2つの処理をm回繰り返すことで、機械学習モデルとしての表現力を向上させた。
繰り返しになるが、QCLに決まった回路構成は存在せず、あくまで上記は設計の一例に過ぎない(論文では機械学習に適した回路構成を予備検討・議論したので、興味のある方はそちらを参照)。
2.4 QCLのPythonによる実装
細々と理論を記載したが、上記のQCL回路に関しては、量子ゲートシミュレータでのPythonの実装を公開している。
基本コードは以下の通り。
from QCLRegressor.regressors.StandardQCLRegressor import StandardQCLRegressor
from QCLRegressor.gates.CNOTRotationGates import CNOTRotationGates
from QCLRegressor.Encoders.XYEncoder import XYEncoder
from QCLRegressor.gates.Observable import ZObservable
#X,yの定義
X=...
y=...
x_dim=2 #xの次元
n_qubit=2 #量子ビットの次元
depth=3 #量子回路の深さ
#モデル定義
model=StandardQCLRegressor(x_dim=x_dim,
n_qubit=n_qubit,
encoder=XYEncoder(n_qubit),
observable=ZObservable(n_qubit=n_qubit,coeff=2), #coeffはハイパーパラメータ
vqe_gates=CNOTRotationGates(n_qubit=n_qubit,depth=depth))
#モデル訓練
model.fit(X,y)
#推論
model.predict(X)3. QCLの回帰性能の評価
3.1 シミュレータと実機の比較
簡単なサイン波についてQCLで回帰を行った結果を以下に示す。

State vectorは、Qulacsと呼ばれるライブラリを用い、状態ベクトルを古典コンピュータで正確に計算した結果、simulated samplingはシミュレータでyをサンプリングした結果、quantum samplingは量子シミュレータの実機でQCLを行った結果を示す。
量子コンピュータの実機としては、IBM Quantumなどのクラウドサービスが存在する。数量子ビットであれば、無料で利用できる。
State vectorを用いた場合、問題なく回帰ができていることが分かった。Simulated samplingはややノイズが乗る結果となったが、これはサンプリング回数(やコード実装)の問題かもしれない。サンプリングを無限回まで増やすなどすれば、理論的にはstate vectorの結果と一致する筈である。
一方、quantum samplingでは訓練・テストデータともにズレが目立った。これは計算時のノイズに由来するものである。量子コンピュータの実機を使いこなすのは、容易ではない。
そのため、以下の検討では、state vectorによる計算結果を用いた。
3.2 QCLと古典コンピュータのアルゴリズムの比較
論文ではいくつかの1次関数に対して回帰を行った。QCLに対するコントロールとして、ガウス過程(GPR)、ニューラルネットワーク(MLP)などを選択し、ハイパーパラメータを変えながら性能を比較した。

解析の結果、少なくとも今回の回路構成においては、QCLが「なめらかな曲線」に対して優れた回帰性能を示しやすいことが明らかになった*。
*回路構成を変えれば、回帰特性は変化しうる点に注意
3.3 有機化合物の物性予測
有機化合物に対するいくつかの標準的なデータセットを用い、QCLの回帰性能を評価した。分子構造はRDKitモジュールの標準的な記述子アルゴリズムを用いて数値情報に変換した。
QCLには種々の制約条件が存在するため、以下の処理を行った。
a) RDKitによって200種類程度のパラメータが得られるが、QCLの量子ビット制約の都合上、200次元の入力を扱うことはできない。そこで、説明変数は主成分分析のアルゴリズムを用い、8次元まで圧縮した。
b) QCLの出力域は-1~+1に限られるため、目的変数もこの範囲内に正規化した。
c) 推論速度に制限があるため、元のデータベース(>数千点)から数件~数百件程度のサンプルをランダムに選択し、回帰性能を評価した。
融点に関する回帰結果の例を図a)に示す。この評価では、テストデータのyが訓練データの外に存在する、いわゆる外挿予測の性能を評価した。QCLのMSEは0.25であった。これに対し、ランダムフォレスト(RFR)では0.35、サポートベクタマシン(SVR) 0.30、ベイジアンリッジ(BYR) 0.57、部分的最小二乗回帰(PLS) 0.94、ガウス過程(GPR) 0.61と大きな誤差を示した。
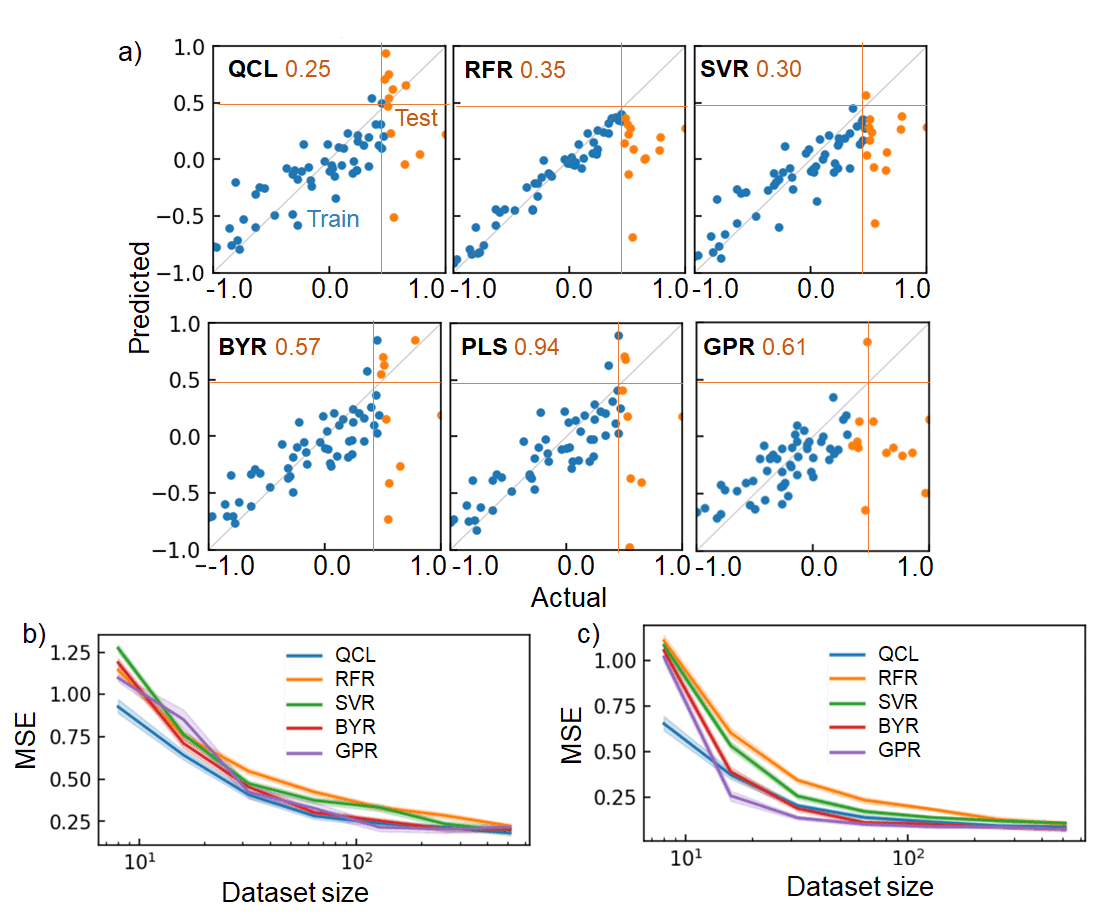
統計的な優位性を検証するため、学習・テストデータセットをランダムに変えながらMSEを評価した(図b)。データセットのサイズが30程度までは、QCLが有意に優れた回帰性能を示すことがわかった。データ数が増えると、アルゴリズムの違いは小さくなった。ESOLと呼ばれるパラメータにおいても、同様の傾向が得られた(図c)。
一方、図示はしないが、LipoやSolvと呼ばれるパラメータではQCLが劣った性能を示す場合があった。
QCLが優れた性能を示す理由は、調査中であるが、高次元データにおいても、「なめらかなデータ分布を持つ系」に対して、相性が良いと推察している。
3.4 QCLの回帰性能に関する特徴と課題
QCLの特徴について議論する。
特長は以下のとおりである。
なめらかな一次元関数や一部の化合物データセットにおいて、般的なアルゴリズムに対する回帰性能の一部優位性が観測された
欠点は以下のとおりである。
計算コストが高い
通常のワークステーションでのシミュレーションでは8次元程度が限界
量子コンピュータの実機ではノイズが乗りやすい
扱える次元数に制限
現状では数~数十次元程度
出力域に制限
-1 ~ +1
logit関数を噛ませるなどの工夫は可能
計算時間
実機であっても、1件の予測に100~1000回程度のサンプリングを要する
1万件の推論には100万ー1000万回のサンプリング
QCLの学術的な特徴は以下のとおりである。
2^N次元という超膨大な複素空間上で演算処理をするので、何か面白い性質や表現力を有している可能性がある
出力が常に-1~+1の範囲に収まるよう、正則化が自動でなされている
量子力学に特有の情報・系をうまく入力すれば、古典系よりも良い予測性能を得られる可能性がある
4. まとめ
本稿では、量子回路学習(QCL)の基礎となる理論と、化学分野における利用検討の結果について記した。計算コストや入力次元の制限、ノイズの問題など、課題は山積みであるが、なめらかな関数への優れた回帰性能など、QCLの特徴ある性質が明らかになり始めている。現在は詳細な特性研究を進めているほか、専用シミュレータによる量子ビット数の拡大も検討中である。
より長期的な視点に立つと、ゲート型マシンの性能は年々増加していくと見込まれる。新たな用途が次々と出現するかもしれない。莫大な計算コストや電気代が課題となっている深層学習・大規模言語モデルへの貢献など、全く新しいブレイクスルーに繋がる可能性もあり、今後も継続的な基礎研究が欠かせない。
