vicuna-13bで embedding vectorの計算 (& GPT・RWKVとの比較)
背景
背景はこちらの記事と同じです
最近は、GPTが流行ってます
しかしGPT-3.5以降はfine tuningが執筆時点でできません
なので、オリジナルデータを学習させるには、少し工夫が必要です
お、これはムッチャ分かりやすいな https://t.co/3YtaUR8lyQ
— Masanori Kusunoki / 楠 正憲 (@masanork) April 22, 2023
要するに、文章のembedding vectorを計算する必要があります
しかし、GPTのAPIは地味に値段が高いため、pdfが100個くらいあったりすると、破産する恐れが出てきます
目的
最終的な推論はGPT-3.5 or 4にやらせるとして、embedding vectorの計算は、もう少しローコスト・低性能なLLMで良いのではないかと、誰しも考えるはずです
或いは、google検索のような、index検索を使うのも手です
ただしこの場合は、言語を跨いだ検索などが難しそうです
そこで、一般のご家庭のPCでも動き、日々タケノコの如く報告されるLLMの中でも、群を抜いていると評判のvicuna-13bを動かしてみることにしました
ついでに、RWKV-7b、GPTのAPIと比較してみました
vicunaのセットアップ
いろんなやり方があるようですが、以下のやり方が楽でした
from transformers import AutoTokenizer, AutoModelForCausalLM
tokenizer = AutoTokenizer.from_pretrained("eachadea/vicuna-13b-1.1")
model = AutoModelForCausalLM.from_pretrained("eachadea/vicuna-13b-1.1",device_map = 'auto')device_map = 'auto'としておくと、適当にGPUを割り振ってくれました。研究室にある、RTX3090 x2 (ご家庭用のGPU)を搭載したマシンで読み込めました。1枚だとメモリ不足でエラーが出ました。
動作確認
まずはpromptに応答するかを見てみます。
promptの作成function。 vicunaがこちらの形式のpromptで学習しているかは、チェックしていませんのでご注意
def generate_prompt(instruction, input=None):
if input:
return f"""Below is an instruction that describes a task, paired with an input that provides further context. Write a response that appropriately completes the request.
# Instruction:
{instruction}
# Input:
{input}
# Response:
"""
else:
return f"""Below is an instruction that describes a task. Write a response that appropriately completes the request.
# Instruction:
{instruction}
# Response:
"""推論
# 推論
prompt=generate_prompt("answer the question", "何故雨が降るのか?")
input = tokenizer.encode(prompt, return_tensors="pt")
output = model.generate(input, do_sample=True, max_length=200, num_return_sequences=1)
ans=(tokenizer.batch_decode(output))
print(ans[0].replace(".\\n\\n2.","\\n"))
回答はこちら
# Instruction: answer the question
# Input: 何故雨が降るのか?
# Response: 雨が降る理由は、大気圏が低いほど気泡が拡大するとり、その気泡が太陽光を遮蔽してこだわりやすく、水滴が気泡から蒸着させられて雨となります。また、雨が降ることで土壌が濕まれ、植物が生きやすくなり、
そこそこ知的で意味不明な回答が返って来ました。max_lengthを増やすと、更に長い回答が返ってくるはずです。ただしこのレベルの回答でも、1minほどの計算が必要でした。GPT3.5, 4の回答速度の速さには驚くばかりです
潜在ベクトルの計算
入力テキストの長さに応じて、hidden_statesの次元が変わります。今回はとりあえず、適当にaxis=1で平均値を取ることで、vectorの次元を固定することにしました。
以下の関数で出力されるvectorは209920次元でした。GPTやBERTでは1500次元程度のベクトルを出す機能があります。多量のデータを扱う場合は、うまく圧縮するアルゴリズムを作る必要がありそうです。
import numpy as np
import torch
def calc_vec(input_text, model, tokenizer):
input_ids = tokenizer.encode(input_text, return_tensors="pt")
model.eval()
with torch.no_grad():
outputs = model(input_ids, output_hidden_states=True)
#list形式でtensorが入っているoutputsを1次元のnumpyに変換
vec_list=[]
for v in outputs[-1]:
mean_v=v.mean(axis=1)
vec_list.append(mean_v.numpy().flatten())
vec=np.array(vec_list).flatten()
return vecコサイン類似度を計算してみます
from tqdm import tqdm
import numpy as np
text_list=[
"吾輩は猫である",
"汝の名は女だ",
"I am a cat",
"ピペットで試薬を三回分取した",
"アセトンは有機溶媒である",
"非プロトン性溶媒として、THF、トルエンなどが挙げられる",
"トルエンをこぼしてしまいました",
"私は猫です",
"私は犬です",
"日本的霊性は,鎌倉時代に禅と浄土系思想によって初めて明白に顕現し,その霊性的自覚が現在に及ぶと述べる.",
]
vec_list=[calc_vec(i,model,tokenizer) for i in tqdm(text_list)]
target_vec=vec_list[0]
from scipy import spatial
def cos_sim(a, b):
return 1 - spatial.distance.cosine(a, b)
cos_sim_list=[cos_sim(target_vec,i) for i in vec_list]
for i in np.argsort(cos_sim_list)[::-1]:
print("{:.3f}".format(cos_sim_list[i]),text_list[i])「吾輩は猫である」とコサイン類似度の高い文字列は以下の通り by vicuna
1.000 吾輩は猫である
0.977 私は猫です
0.975 私は犬です
0.970 汝の名は女だ
0.959 I am a cat
0.935 アセトンは有機溶媒である
0.934 トルエンをこぼしてしまいました
0.927 ピペットで試薬を三回分取した
0.807 非プロトン性溶媒として、THF、トルエンなどが挙げられる
0.600 日本的霊性は,鎌倉時代に禅と浄土系思想によって初めて明白に顕現し,その霊性的自覚が現在に及ぶと述べる.
RWKVよりも賢そうです。 RWKVの結果はこちら。
(注 7Bモデルを使いました。14Bモデルを使ったらもっと良くなるかもしれません)
1.000 吾輩は猫である
0.950 汝の名は女だ
0.950 アセトンは有機溶媒である
0.946 トルエンをこぼしてしまいました
0.942 私は猫です
0.941 ピペットで試薬を三回分取した
0.917 私は犬です
0.905 非プロトン性溶媒として、THF、トルエンなどが挙げられる
0.882 I am a cat
0.859 日本的霊性は,鎌倉時代に禅と浄土系思想によって初めて明白に顕現し,その霊性的自覚が現在に及ぶと述べる.
RWKVは、「吾輩は猫である」の文語調に引きずられ、「汝の名は女だ」というハムレット的フレーズに親近感を覚えてしまいました。
一方、vicunaでは、「吾輩は猫である」に最も近いフレーズとして、「私は猫です」を選びました。
ただ、その次に高い類似度は「私は犬です」、「汝の名は女だ」となっており「I am a cat」が追いやられてしまいました。日本語を取るか、意味を取るか、の葛藤があったのかもしれません。
ついでに、GPTでも計算してみます。似たような性能でした。が、スピードはGPTが圧倒的でした。
def calc_vec(text):
vec= openai.Embedding.create(input = text, model="text-embedding-ada-002")['data'][0]["embedding"]
return np.array(vec)1.000 I am a cat
0.974 私は猫です
0.974 私は犬です
0.971 汝の名は女だ
0.959 吾輩は猫である
0.924 アセトンは有機溶媒である
0.918 トルエンをこぼしてしまいました
0.908 ピペットで試薬を三回分取した
0.763 非プロトン性溶媒として、THF、トルエンなどが挙げられる
0.499 日本的霊性は,鎌倉時代に禅と浄土系思想によって初めて明白に顕現し,その霊性的自覚が現在に及ぶと述べる
次に、「I am a cat」と類似度の高い文字列を計算してみます。
vicunaの結果はこちら。そこそこの性能ですね。
1.000 I am a cat
0.974 私は猫です
0.974 私は犬です
0.971 汝の名は女だ
0.959 吾輩は猫である
0.924 アセトンは有機溶媒である
0.918 トルエンをこぼしてしまいました
0.908 ピペットで試薬を三回分取した
0.763 非プロトン性溶媒として、THF、トルエンなどが挙げられる
0.499 日本的霊性は,鎌倉時代に禅と浄土系思想によって初めて明白に顕現し,その霊性的自覚が現在に及ぶと述べる.
RWKVの結果はこちら。 ほぼ同じ。
1.000 I am a cat
0.914 私は猫です
0.911 私は犬です
0.899 汝の名は女だ
0.882 吾輩は猫である
0.849 トルエンをこぼしてしまいました
0.841 アセトンは有機溶媒である
0.826 ピペットで試薬を三回分取した
0.768 非プロトン性溶媒として、THF、トルエンなどが挙げられる
0.706 日本的霊性は,鎌倉時代に禅と浄土系思想によって初めて明白に顕現し,その霊性的自覚が現在に及ぶと述べる.
GPTの結果はこちら。 パーフェクトな回答でした。素晴らしい。
意味を読み取る力が高いのか、それとも文語体の文章を読む能力が高いのか、要因は調べる必要がありそうです。
(今後、メインのタスクで特に文語体のデータを学習させる予定はないので、そもそもベンチマークが不適切だったことに、今更気づきました)
1.000 I am a cat
0.883 私は猫です
0.875 吾輩は猫である
0.829 私は犬です
0.753 汝の名は女だ
0.730 トルエンをこぼしてしまいました
0.727 ピペットで試薬を三回分取した
0.707 アセトンは有機溶媒である
0.694 非プロトン性溶媒として、THF、トルエンなどが挙げられる
0.691 日本的霊性は,鎌倉時代に禅と浄土系思想によって初めて明白に顕現し,その霊性的自覚が現在に及ぶと述べる.
おまけ: 二次元空間への転写
最後に、vicunaから出てきた高次元ベクトルをPCAやMDSで二次元空間に飛ばしてみます。
正直、微妙な結果となりました。コサイン類似度はまともなので、情報圧縮の方が上手くいっていない印象です。
from sklearn.manifold import MDS
import matplotlib.pyplot as plt
#PCAで圧縮
from sklearn.decomposition import PCA
reducer=MDS(n_components=2)
#reducer=PCA(n_components=2)
comp_vec=reducer.fit_transform(np.array(vec_list))
plt.scatter(comp_vec[:,0],comp_vec[:,1])
for i, txt in enumerate(text_list):
plt.annotate(txt, (comp_vec[i,0],comp_vec[i,1]),size=10)
plt.show()PCA
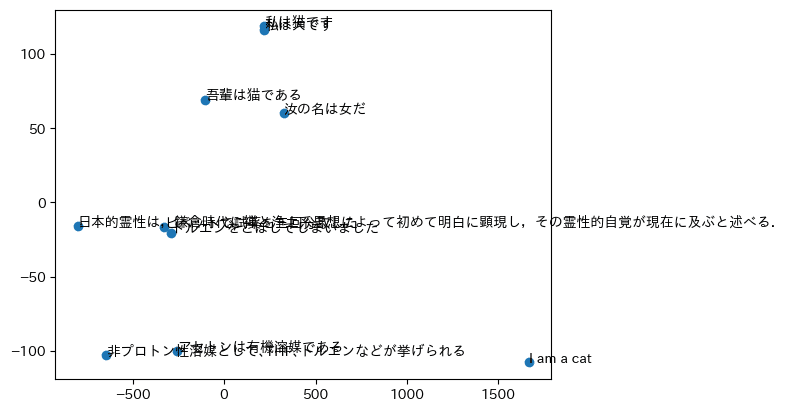
MDS

まとめ
vicunaを使うことで、テキストのembedding (latent) vectorを計算可能でした
比較精度は、GPT > vicuna > RWKV となりました。しかし、劇的な差は見られませんでした
計算コストと精度のコストパフォーマンスを考えると、RWKV(あるいは更に低コストなモデル)でも、vector計算という用途では十分かもしれないという思いに至りました
