
足し算をどう計算するか
昔バズっていたさくらんぼ計算について、そろばんと似ているな〜なんでかな〜と考えていたのですが、どちらも補数で計算していることに気がつきました。しかしそろばんは全て補数で計算しているわけではありません。そこで、そろばんの計算方法について、水道方式の素過程の表を使って整理してみました。また、足し算に関する水道方式の文献についても調べてみました。
さくらんぼ計算について
さくらんぼ計算は主にくりあがりくりさがりの計算で用いられる指導方法です。twitterなどで検索して読んでいくと、え?結局良いの?悪いの?どっちなの?と混乱します。
そろばんについて
そろばんは、5玉1個と1玉4個で一桁を表す計算道具です。
子どもの頃、わたしは近所の教室に通ってそろばんの練習をしていました。
本文での「そろばんでは」という表現は、わたしの習ったそろばんの計算方法のことです。
似ているな〜と思ったこと
さくらんぼ計算とそろばんは、補数で計算していることが似ているなと思いました。ここでの補数はある数に足して10になる数のことを言っています。
くりあがりのある足し算でのさくらんぼ計算では、足す数を「足される数が10になる数」と「残り」に分けて、10と残りを足して答えを出します。このような計算方法を、10の合成というそうです。
例として、19+7で考えてみます。2行目で7を(1+6)に分けます。
19+7
=19+(1+6) ←足す数を「足される数が10になる数」と「残り」に分ける
=20+6
=26
一方そろばんでは、足される数から「足す数が10になる数」を引いて10を加えて答えを出します。同じ例で考えます。
19+7
=19+(-3+10) ←足される数から「足す数が10になる数」を引いて10を加える
=16+10
=26
この、ある数が10になる数=補数を扱う点が似ているな〜と思いました。
脱線しますが、情報系なので補数といえば2進数の2の補数と1の補数のことがパッと浮かびます。同じく、10進数には10の補数(基数の補数)と9の補数(減基数の補数)があり、ここで扱っているのは10進数の10の補数です。
似てないな〜と思ったこと
どっちも補数なのか〜で終わりかと思ったのですが、そろばんでは補数で計算しない足し算があります。
例として16+6で考えてみます。
さくらんぼ計算の場合、例によって補数を使用します。以下の通り、2行目で6を(4+2)に分けます。
16+6
=16+(4+2) ←足す数を「足される数が10になる数」と「残り」に分ける
=20+2
=22
そろばんの場合、足される数に「足す数から5を引いた数」を加えて、5を引いて10を加えます。以下の通り、同じ例で考えます。
16+6
=16+(1-5+10) ←足される数に「足す数から5を引いた数」を加えて、5を引いて10を加える
=17-5+10
=12+10
=22
この2行目の()内の1-5を-4と置けば補数と言えるのかもしれませんが、実際のそろばんの動きを考えると1を加算、17から5を減算、10を加算という感じで補数4は出てきません。
以上のように、そろばんは10や5のまとまりで計算をすることがあります。この5と残りに分けて考える方法は二五進法といいます。
そろばんの計算方法はどこで切り替わるのか
基本的にそろばんの計算方法は二五進法ですが、どこで10の補数に切り替わるのか調べてみました。ここでは、水道方式の素過程の表を使用します。素過程とは、0~9までの一桁の計算のことです。
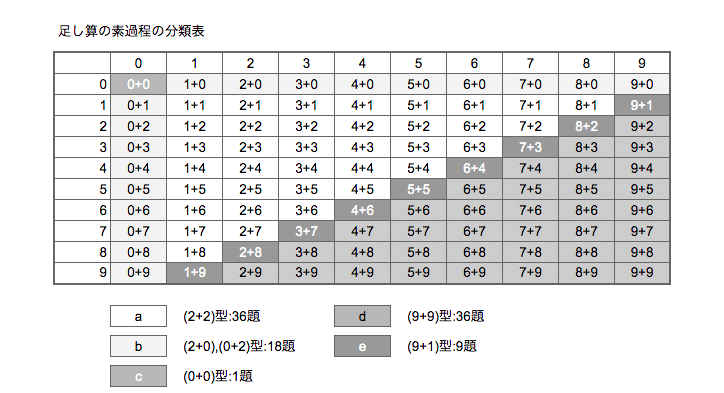
足し算の素過程は100パターンあり、やさしい順でa~eに分類されます。(bは本来は別々の型ですが勝手にまとめました)これは2-9分類法と言います。
a (2+2)型:くりあがりのない問題
b (2+0), (0+2)型:くりあがりがなく式が0を含む問題
c (0+0)型:くりあがりがなく式が0を含む問題
d (9+9)型:くりあがって答えが0を含まない問題
e (9+1)型:くりあがって答えが0を含む(和が10になる)問題
さらに、d (9+9)型を5種類に分類しました。

くりあがりのある足し算は、やさしい順にd1~d5となります。
d1 (7+5), (5+7)型:くりあがって式に5を含む問題
d2 (7+7)型:くりあがって式が5と残りに分けられる値の問題(両方)
d3 (8+7)型:くりあがって答えが5を含む(和が15になる)問題
d4 (9+4), (4+9)型:くりあがって式が5と残りに分けられる値の問題(片方)
d5 (9+9)型:くりあがって答えが15より大きい問題
この分類上でそろばんの計算方法を考えると以下のようになりました。
a, b, cは二五進法
d1は二五進法
d2は二五進法
d3は10の補数
d4は10の補数
d5は10の補数
eは10の補数
以上のことから、足し算の素過程の分類のやさしい順で、そろばんの計算方法は、d2までは二五進法、d3からは10の補数に切り替わることがわかりました。
2-9分類法を使うことできれいに切り分けることができましたが、そろばんを使わない人にとっては意味不明かと思います。そろばんを使う人もこの順番を意識していることは全くなく、ただ玉の動きを考えるとそういう計算をしているというだけのことです。筆算や暗算する場合も、わたしは計算方法をそろばんと同じように切り替えているようでした。ですが、本当に初めて足し算を学ぶ子どもに同じ方法で計算させるのは厳しかろうということは想像できます。
計算方法をどちらかに統一できないのか
人それぞれ計算方法はあるかと思いますが、二五進法を使うのか10の補数を使うのかに統一するのも手段の一つと言えます。
10の補数を使うのに統一しているのが、さくらんぼ計算です。
さくらんぼ計算はくりあがりのある計算のため、対象となるのは2-9分類法のd (9+9)型とe (9+1)型です。くりあがらない計算は、おそらく二五進法を使用していると思います。
一方、二五進法を使うのに統一しているのが、水道方式です。
独特な計算方法になり、計算のステップ数も増えますが、5のかたまりを作るというルールで曖昧さが少ないのがメリットかと思いました。計算方法については、以下リンクを参照しました。
水道方式の足し算について
最後に、水道方式についての書籍から参考になった文章を引用します。
二五進法は水道方式には5・2進法/五・二進法(ゴニシンホウ)として記載してあります。5を束にしたものの2進法と5進法の組み合わせなので同じことと解釈していますが、なかなか検索に引っかかりませんでした。
当初の水道方式のくりあがりのある足し算は10の補数で説明を行っていて、1970年代の本から順次五・二進法で計算が説明されています。変更した経緯については以下に詳しいです。
(水道方式をめぐって, 遠山啓 p.80より引用)
(省略)その大会に、われわれとはぜんぜん関係のない人ですが、鳥取県の人で、知恵おくれの子を教えている人が参加していて、そのときに、いま、われわれが"五・二進法"、といっているのにひじょうに近い方法を発表した。それは、タイルなんかもちろん使っていないのですが、5としてローマ数字の"V" を使った。"Vといくつ"ということで教えたら、知恵おくれの子はたいへんよくわかったというような報告がありまして、なるほど、これはたいへんいい方法だと思って、5のかたまりを途中で考える方法というのを、そのあたりからやりだしたわけです。最初のものよりは、現在のように、5のかたまりを考えるほうがよりいいということは、だいたい証明されていると思います。(省略)
10の補数で説明していた頃の計算方法は、さくらんぼ計算に似た感じで枝分けしてあります。
(算数はこわくない, 遠山啓 p.133より引用)
[くりあがりのある計算]
さて (9+9)型(9+1)型の計算の指導です。
(9+9) 型の計算の方法として数えたしの方法と基数を分解して10を合成する方法の2つがあります。「数えたし」では、あとで2ケタ、3ケタの計算になったときには、もう使えませんので、はじめから「基数を分解して10の合成」の方法で指導していただきたいと思います。
それは、どんな方法でしょうか。
[[基数の分解・10の合成]]
例として、8+6=14を考えてみましょう。下の図を見てください。
8は、10になるために、あと2が必要です。これを10に対する補数といいます。そこで、8+2=10と、10を合成しますが、基数の6は、2と4とに分解されてしまったわけです。そこで、その4を10に加えて、14という答えが出るわけです。
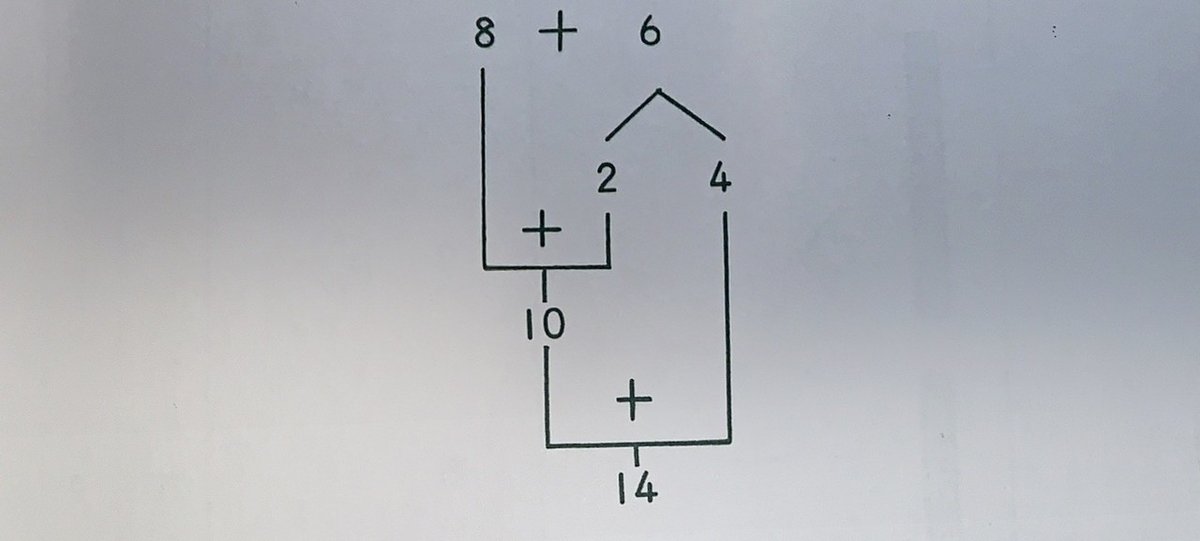
出典:算数はこわくない, 遠山啓 p.133
(算数はこわくない, 遠山啓 p.135より引用)
被加数を見て、その10に対する補数がすぐわかるように、つぎのような問題をやらせることも、子どもの力をつけます。

出典:算数はこわくない, 遠山啓 p.135
5・2進法は、くりあがりのない足し算(素過程のa,b,c)と、くりあがりのある足し算(素過程のd1)に限って説明されていました。
(算数はこわくない, 遠山啓 p.136より引用)
また、8+5などのときは(5+3) + 5というように8を5+3に分解して、13という答えを得る5・2進法が、すぐれた力を発揮しますので、つぎのような問題をやらせることも、たいせつです。

出典:算数はこわくない, 遠山啓 p.136
素過程の分類に使用した、2-9分類法については以下からきているそうです。
(水道方式とはなにか, 遠山啓 p.258より引用)
追記1ーーいちいち”I位数とI位数の加法でくりあがらないもの”などと言葉で言っていては大変なので、数字の2と9を利用して、くりあがらないのは2+2とか2+2(筆算の表記)で、くりあがるのは9+9とか9+9(筆算の表記)で表示することにする。これが”2-9分類法”と言われるものである。
具体的な二五進数を使った計算方法についても、文献(おそらく"水道方式による計算体系 増補")にあたりたかったのですが、地域の図書館もAmazonもブックオフもメルカリも紀伊國屋にもなく、大学図書館はコロナで使えないということで諦めました。
まとめ
そろばんの計算方法について、水道方式の素過程の表を使って整理してみました。結果として、やさしい計算の順で二五進法から10の補数に計算を切り替えていることがわかりました。
水道方式はちょっと古い本ですが、昔はそれまで算数を分析・分類した人がいなかったし、筆算も普通のことではない世の中だったというのが知れて面白かったです。
足し算は、今回のような計算をしたり、掛け算をして引いたり、答えを暗記したり解き方は様々あります。子どもの頃のことを思い出すと、変わった解き方をすると先生が「これは○○という解き方だね」と褒めてくれて自信をつけていました。将来小学校に上がる子どもも、そんな先生に当たるといいな〜と思いました。
