
【エントロピーと秩序(0)】熱力学からエントロピーを考えたい
こんにちは('ω')ノ
熱力学の勉強をする中で最も謎な概念であるエントロピーについて今一度歴史を学びながらその意味を学んでおこうと思い本書を手に取りました。
これから数か月間はエントロピーについて本書で読んだ内容をまとめていこうと思います。
本書の内容をただまとめるだけではなく、補足を加えながらまとめていきます。決して誰かに読まれることを想定して書いていないためわかりにくい箇所が多々ありますがご了承ください_(._.)_
エントロピーの定義
熱力学は高校・大学で学んだため基礎的な知識はあります。
大学ではじめてエントロピーについて学ぶのですが、定義式はわかったとしてもどういった意味を持っているのかはいまいちわかっていません。
まずはエントロピーの定義式を書いておきましょう
エントロピーの定義
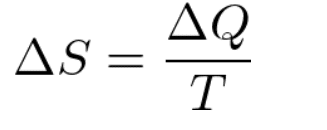
エントロピーは吸収した熱量ΔQを温度で割ったものという式で定義されています。これは熱力学でのエントロピーの定義式です。
統計力学や情報理論においてエントロピーは違う形で定義されています。
統計力学でのエントロピーの定義式はこちらです。
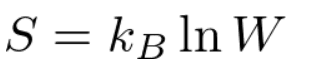
Wが状態の取りうる場合の数です。
エントロピーはしばしば「無秩序さ、ランダムな具合」など「エントロピーが大きい=ぐちゃぐちゃの状態」というように、理系界隈では日常でも使われる用語であります。
それは統計力学のエントロピーが取りうる状態の数Wの対数で書けるからです。部屋のモノの配置が整っていてきれいに整列されていれば取りうる場合の数は少なく、よってエントロピーが小さい。部屋にモノが無造作に置かれている、「このモノはどこにおいても構わない」というカオス状態であれば取りうる場合の数が多い、よってエントロピーが大きい。このように表現されます。
しかし、厳密には状態の数とエントロピーは対数の関係にあって比例関係ではありません。その辺もエントロピーの理解には引っかかる部分がありますが、もっと引っかかる部分は統計力学のような状態の取りうる場合の数というのは分子というミクロな詳細について考えている点です。
エントロピーが出てきた当初、熱力学は工業機関(熱機関)において発展した概念であって、このときは熱素という間違った概念はあったものの、現代の分子などの理論がまだ確立されていなかった頃に出てきた概念です。
とすれば、エントロピーは統計力学での意味の「無秩序さ」という理解ではなく熱力学から理解しなくてはならないと考えられます。
エントロピーの意味
熱力学でのエントロピーの意味は、「自発的変化において自然に起こりうる方向を指し示すもの」だと解釈されています。
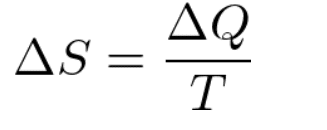
つまり、上式を計算した際に状態1より状態2の方がエントロピーの値が小さいとき、放っておくと自然に起こりうるのは状態1から状態2への変化だということです。決して、逆にはならないということがエントロピーからわかるというのです。
エントロピーとの関連性
エントロピーは熱力学の多くの法則とも関連している概念です。
●熱力学第二法則
●クラウジウスの法則
●トムソンの法則
●カルノーの原理
●エントロピーの原理
●カルノーサイクルやオットーサイクル
●第二種永久機関は存在しない
●熱と仕事は非対称
●エントロピー増大則
どこから取り上げて理解を進めていけば良いのか悩ましいところです。
これらを単独で記憶しようとすると「熱力学はずいぶんと多くの法則があるのだなー」という印象を受けてしまいます。
現象は数少ない法則で記述できるから美しいのであって、「この現象にはこの理論(法則)、あの現象にはこの理論(法則)」としてしまってはもはやそれは法則ではないのでは?と疑問に持たれそうです。
しかし、上で書いた原理や法則は関連性があります。
おおまかにまとめて熱力学第二法則と呼ばれています。
熱力学には4つの法則があり(熱力学第ゼロ法則、熱力学第一法則、熱力学第二法則、熱力学第三法則)、熱力学第二法則が一番初めにできた法則であることを考えると熱力学の最も基礎的な法則を表していると言えるでしょう。
というわけで、エントロピーは熱力学を理解するうえで最も重要な概念ではないかと思い本書を手に取って学び始めました('ω')ノ
本書を読んではnoteにまとめて、自分の中でまとまったらブログ記事としてアップする予定です(^^)/
Twitter➡@t_kun_kamakiri
Instagram➡kamakiri1225
ブログ➡宇宙に入ったカマキリ(物理ブログ)
ココナラ➡物理の質問サポートサービス
コミュニティ➡製造業ブロガー
