【過去問解答】筑波大学医学部編入試験【数学・化学・英語】
この記事では令和5年度~令和2年度分について、筑波大医学部学士編入試験過去問のオリジナル解答を無料公開しています。
数学・化学・英語の過去問解答や出題傾向について解説します。
感想やご要望等ございましたらコメントいただけると嬉しいです!
過去問から見る出題傾向
数学
高校範囲の数学も出題されます。特にベクトル、極限、微積などが頻出なので、数学ⅡBや数学Ⅲの範囲を復習しておくとよいでしょう。
また大学範囲の数学については線形代数や統計学(特にポアソン分布が頻出)を勉強するのがオススメです。
令和5年度の過去問解答
過去問はこちら
👇英語の本文が見たい方はTwitterでDMいただければ無料で対応します!
kamo(@kamo_exam)さん / Twitter
英語
準備中
数学
準備中
化学
問題1
問1
(ア): 12
(イ): d
(ウ): 両性
(エ): 白色
(解説)
(イ) 第4周期の遷移元素の特徴として,
最外殻電子軌道(4s軌道)に先に電子が2つ埋まり(CrとCuは例外的に1つ),
そのあと一つ内側の3d軌道に電子が埋まっていく,
つまり多くの(Cu以外の)遷移元素の3d軌道は電子で完全に満たされていない,という特徴があります。
亜鉛は最外殻の4s軌道に電子が2つ埋まっていて,
その内側の3d軌道にも電子が埋まっている,という点で特徴的な原子です。
(エ) 硫化物の沈殿は黒色…と反射的に答えたいところですが,ZnSは白色沈殿です。黒色以外になる硫化物は他にも,CdS(黄色)やMnS(淡赤色)などがあります。
問2
(1) 黄銅
(2) トタン
(解説)
ちなみに銅とスズの合金は青銅,スズでメッキした鋼板はブリキです。
こんがらがりやすいので注意しましょう。
問3
$${\mathbf{Zn+2HCl \rightarrow ZnCl_2+H_2 \uparrow }}$$
$${\mathbf{Zn+2NaOH+2H_2O \rightarrow Na_2[Zn(OH)_4]+H_2 \uparrow }}$$
(解説)
水酸化ナトリウムと反応すると錯イオンであるテトラヒドロキソ亜鉛(II)酸イオンとなって水溶します。
問4 $${\mathbf{7.43[g/cm^3]}}$$
(解説)
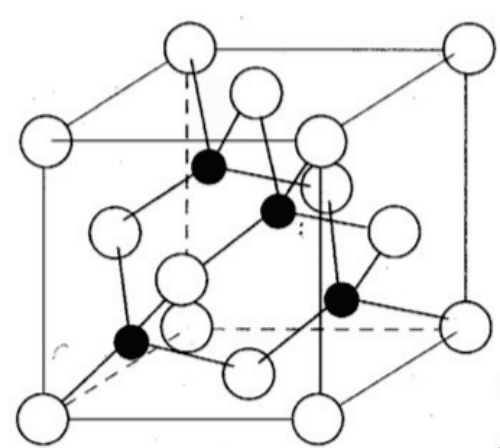
六方最密充填構造の単位格子(平行四辺形の四角柱)の一辺が$${a}$$なので,
底面積は正三角形2つ分で$${\displaystyle\frac{\sqrt{3}}{4}a^2\times 2=\displaystyle\frac{\sqrt{3}}{2}a^2}$$。
高さは$${c}$$なので単位格子の体積は$${\displaystyle\frac{\sqrt{3}}{2}a^2c}$$。
また単位格子内の原子数は2個なので,求める密度は
$${\displaystyle\frac{2\times 65.4 \times 2}{\sqrt{3}\times (0.26\times 10^{-7})^2\times (0.5\times 10^{-7})\times 6.02\times 10^{23}}=7.431…\simeq 7.43}$$
問5 $${\mathbf{Ag^+, Cu^{2+},Hg^+,Pb^{2+}}}$$
(解説)
硫化物イオン$${\rm{S^{2-}}}$$は酸性では濃度が薄く,塩基性だと濃くなります。(2段階電離の平衡による。)
つまり酸性条件下では$${\rm{[S^{2-}]}}$$が低いので沈殿は生じづらくなります。
こうした酸性条件下でも,
イオン化傾向の小さいイオンは沈殿を生じますが,$${\rm{Zn^{2+},Fe^{3+},Mn^{2+}}}$$などのイオンは沈殿しません。
$${\rm{Zn^{2+},Fe^{3+},Mn^{2+}}}$$は塩基性にすると沈殿を生じるようになります。
そのとき特に,$${\rm{Fe^{3+}}}$$は$${\rm{Fe_2S_3}}$$ではなく$${\rm{FeS}}$$として沈殿することに注意しましょう。
($${\rm{H_2S}}$$によって$${\rm{Fe^{3+}がFe^{2+}}}$$に還元されるためです。)
問6
問題2
問1
(ア): 正
(イ): 陽
(ウ): 負
(エ): 陰
(オ): 陰
(カ): 陽
問2 (a), (c), (d)
問3
陽極: $${\mathbf{2Cl^- \rightarrow Cl_2 \uparrow + 2e^- }}$$
陰極: $${\mathbf{2H_2O+2e^- \rightarrow H_2 \uparrow + 2OH^- }}$$
問4 $${\rm{\mathbf{1.24\times 10^{-3}\times t\quad [mol]}}}$$
問5 29分
(解説)
緩衝液の問題です。
少し問題として不親切な点は,
「電気分解による水量の変化は無視してよい」の文言がないことです…
後半でその点の誤差について少し考察します。
pHが5なので$${\rm{[H^+]}=10^{-5}[mol/L]}$$
緩衝液中の$${\rm{[CH_3COOH]=c_a,\quad [CH_3COO^-]=c_s}}$$とすると
弱酸の緩衝液なので,$${\rm{[H^+]=\displaystyle\frac{\rm{c_a}}{\rm{c_s}}K_a}}$$も成り立つ。
$${\rm{K_a}=2.7\times 10^{-5}[mol/L]}$$より
$${\rm{c_a:c_s=1:2.7}}$$
また,加えた酢酸は$${\rm{0.25\times 50\times 10^{-3}=12.5\times 10^{-3}[mol]}}$$なので,
50mlのNaOH+NaCl水溶液に含まれていた$${\rm{[OH^-]}}$$は$${\rm{[OH^-]=12.5\times \displaystyle\frac{2.7}{3.7}\times 10^{-3}[\rm{mol}]}}$$
電気分解において流れた$${\rm{e^-}}$$と発生した$${\rm{OH^-}}$$の物質量は等しく,
電気分解に伴う水溶液の体積の減少を無視すると,
$${\rm{e^-}}$$の物質量について
$${\rm{12.5\times \displaystyle\frac{2.7}{3.7}\times 10^{-3}\times \displaystyle\frac{200}{50} = \displaystyle\frac{2.0\times \rm{t}}{9.65\times 10^{-4}}}}$$
$${\rm{t=29.3412…\simeq 29}}$$
(補足)
水量の減少を無視しないと,答えにどの程度影響があるのか簡易的に考察します。
まず流れた$${\rm{e^-}}$$は$${\rm{0.0365[mol]}}$$程度なので,
$${\rm{H_2O}}$$は等mol反応し,$${\rm{18\times 0.0365=0.657[ml]}}$$程度減少します。(1gの水が水溶液1mlに相当すると概算しています。)
400mlある中での0.657ml(高々0.7mlとします)の誤差なので,
最終的な答えには約-0.4%程度の誤差が生じると推察されます。
すると$${\rm{29.3412\times 0.996 = 29.22…}}$$となり,
有効数字2桁の範囲では答えに影響しないことが確認できます。
問題3
準備中
令和4年度の過去問解答
過去問はこちら
👇英語の本文が見たい方はTwitterでDMいただければ無料で対応します!
kamo(@kamo_exam)さん / Twitter
英語
準備中
数学
問題1
問1 $${\underline{\bm{a=4}}}$$, $${\underline{\bm{x=k, y=\displaystyle\frac{\bm{3}}{\bm{2}}\bm{k+1, z=-k-4}}}}$$
(解説)
$$
{A} = \begin{pmatrix}
1 & 0 & 1 \\
a & -2 & 1 \\
4 & -a & -2
\end{pmatrix}
,
{b}=
\begin{pmatrix}
-a \\
-6 \\
4
\end{pmatrix}
$$
とおくと、与式は
$$
{A}
\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}
=
{b}
$$
と表せる。
ここで、拡大係数行列を$${(A,b)}$$とおくと
未知数は$${x,y,z}$$の3つなので、解が無数にあるためには
$${rk(A)=rk(A,b)=2}$$であればよい。
$$
\begin{pmatrix}
1 & 0 & 1 & a\\
a & -2 & 1 & -6\\
4 & -a & -2 & 4
\end{pmatrix}
\\
→
\begin{pmatrix}
1 & 0 & 1 & -a\\
0 & 1 & \frac{a-1}{2} & -\frac{a^2-6}{2}\\
0 & 0 & \frac{a(a-1)}{2}-6 & 4a+4-\frac{a(a^2-6)}{2}
\end{pmatrix}
$$
より、
$${\frac{a(a-1)}{2}-6 = 0}$$ かつ
$${4a+4-\frac{a(a^2-6)}{2}=0}$$
であればよい。
すなわち$${{\bm{a=4}}}$$
このとき連立方程式の解は無数に存在し、その解は
$${{\bm{x=k, y=\frac{3}{2}k+1, z=-k-4}}}$$
と表せる。
問2 $${\underline{\bm{\theta=\displaystyle\frac{\bm{\pi}}{\bm{6}}}}}$$
(解説)
$${\vec{AB}=(-3,4,5)}$$, $${\vec{AC}=(-2,1,1)}$$
より、$${\vec{AB}\cdot\vec{AC}=15}$$
また、$${|\vec{AB}|=5\sqrt{2}}$$, $${|\vec{AC}|=\sqrt{6}}$$ であるから
$$
\vec{AB}\cdot\vec{AC}
\\=|\vec{AB}||\vec{AC}|\cos\theta
\\=5\sqrt{2}\cdot\sqrt{6}\cdot\cos\theta
\\=15
$$
よって、$${\cos\theta=\frac{\sqrt3}{2}}$$ すなわち $${{\bm{\theta=\frac{\pi}{6}}}}$$
(これは $${0\leq\theta\leq\pi}$$ を満たす。)
問題2
問1 $${\underline{\bm{\displaystyle\frac{1}{4}}}}$$
(解説) 有名問題のため、以下の知恵袋を参照してください(笑)
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1079500890
問2 $${\underline{\bm{\pi}}}$$
(解説) こちらも有名問題。不定積分については以下リンクを参照ください。
分数関数 1/(1+x2) の積分 - あらきけいすけの雑記帳 (hatenadiary.org)
問3 $${\underline{\bm{\displaystyle\frac{241}{60}}}}$$
(解説)
計算ゴリ押しで試験時間を消費させるタイプの問題です。
ゴリ押し以外の計算方法があれば教えてください…
$$
\int^2_1\int^{4-x^2}_0(x+y)dydx
\\=\int^2_1(\frac{1}{2}x^4-x^3-4x^2+4x+8)dx
\\=\bm{\frac{241}{60}}
$$
問題3
問1 $${\underline{\bm{\lambda}}}$$
(解説) ポアソン分布の定義そのものです。以下リンクを参照ください。
https://ai-trend.jp/basic-study/poisson-distribution/p-parameter-derivation/
問2 (小問1)$${\underline{\bm{0.9954}}}$$ (小問2)$${\underline{\bm{0.0015}}}$$
(小問1)
答え自体は誘導の式に代入するだけで求まる。
データセット内のある患者が結核に罹患している確率を$${P_t}$$とすると、
$${P_t=\frac{500}{10,000}=0.05}$$
よって、求める確率は
$${1-(1-{P_t})^{150}\simeq\bm{0.9954}}$$
$${1-(1-p)^n}$$が、なぜ「知人であり、かつ、疾患を持つ患者が含まれている確率」となるのか、についても念のため解説を加える。
上記の表現は「データセット内の知人$${n}$$人を全員連れてきて、そのうち少なくとも1人以上は疾患を持つ確率」と言い換えられる。
$${n}$$人全員が疾患を持たない確率は$${(1-p)^n}$$なので、
題意の確率は$${1-(1-p)^n}$$と表せる。
(小問2)
日本語の表現が曖昧なので、問題に不備があると思われる。
以下の仮定をもとに解く。
仮定①: 「患者が知人であることを特定できる確率は0.1である」という本文中の表現は、
「患者が実際に知人であった際に、その患者が知人であることを正しく特定できる確率は0.1」という意味であると仮定する。
(たとえば、知人のデータを見たけれども、データは匿名化されているので知人だと分からなかった~、となる確率が0.9である、というイメージを仮定している。)
仮定②: 小問2は以下の確率を求めるものと仮定する。
「大腸がんに罹患している、かつ、結核に罹患している患者を無作為に1人選んだ状況を考える。
その条件下で、選ばれた患者が実際に知人であり、かつ、その患者が知人であることを正しく特定できる確率」
(解答)
仮定②のもとで、
題意は「大腸がんに罹患している、かつ、結核に罹患している患者を無作為に1人選んだ状況を考える。
その条件下で、選ばれた患者が実際に知人であり、かつ、その患者が知人であることを正しく特定できる確率」と言い換えられる。
大腸がんを発症すること、結核を発症すること、さらに知人であることの3事象は独立と考えられるので、
患者であろうがなかろうが、無作為に選んだ1人が知人である確率は$${\frac{150}{10,000}=0.015}$$である。
かつ、知人であるその患者について、知人であることを正しく特定できる確率は0.1である。(仮定①)
よって、求める確率は$${0.015\times0.1=\bm{0.0015}}$$
化学
問題1
準備中
問題2
問1
(ア): 水素イオン
(イ): 弱酸
(ウ): 大きく
(エ): ルシャトリエ
(オ): 電離平衡
問2
$${\underline{\mathbf{[C_6H_5COO^-]=\displaystyle\frac{\mathbf{yK_a}}{\mathbf{[H^+]+K_a}}}}}$$
(解説)
$${\rm{[C_6H_5COO^-]}=x[mol/L]}$$とおくと、$${\rm{[C_6H_5COOH]}=y-x[mol/L]}$$なので、
$${\rm{K_a}=\displaystyle\frac{\rm{x[H^+]}}{\rm{y-x}}}$$と表せる。
よって、$${\rm{[C_6H_5COO^-]}=x=\displaystyle\frac{\mathbf{yK_a}}{\mathbf{[H^+]+K_a}}}$$
問3
$${\underline{\mathbf{a=K_a}}}$$
$${\underline{\mathbf{b=-(yK_a+K_w)}}}$$
$${\underline{\mathbf{c=-K_aK_w}}}$$
(解説)
問2に加え、2本の方程式を追加して解く。
1つ目は水のイオン積で、2つ目は電荷の保存則である。(電荷の保存則を初見で思いつくのは難しい…)
水のイオン積については、
$${\rm{K_w}=\rm{[H^+][OH^-]}}$$
また電荷の保存則については、
$${\rm{[C_6H_5COO^-]+[OH^-]=[H^+]}}$$
と表せる。
両辺より$${\rm{[OH^-]}}$$を消去すると、
$${\rm{[C_6H_5COO^-]}=\rm{[H^+]}-\displaystyle\frac{\rm{K_w}}{\rm{[H^+]}}}$$
これが問2の答と同じになるので、
$$
\rm{yK_a[H^+]=[H^+]^2([H^+]+K_a)-K_w([H^+]+K_a)}
$$
すなわち
$$
\mathbf{[H^+]^3+K_a[H^+]^2-(yK_a+K_w)[H^+]-K_aK_w=0}
$$
問4 $${\underline{\mathbf{-log_{10}\displaystyle\frac{\mathbf{-K_a+\sqrt{K_a^2+4yK_a}}}{\mathbf{2}}}}}$$
(解説)
$${\rm{[OH^-]}}$$が無視できるので、
電荷の保存則は $${\rm{[C_6H_5COO^-]}=\rm{[H^+]}}$$ と近似できる。
よって、$${\rm{y=[C_6H_5COOH]+[H^+]}}$$ となる。
これを用いると、
$${\rm{K_a=\displaystyle\frac{\rm{[H^+]^2}}{\rm{[C_6H_5COOH]}}=\displaystyle\frac{\rm{[H^+]^2}}{\rm{y-[H^+]}}}}$$ である。
したがって、
$${\rm{[H^+]^2}+K_a[H^+]-yK_a=0}$$
この2次方程式を解く。
解はモル濃度であり正の値しか取らないので、$${\rm{[H^+]=\displaystyle\frac{\rm{-K_a+\sqrt{K_a^2+4yK_a}}}{\rm{2}}}}$$
よって、
$$
\rm{pH=-log_{10}[H^+]=\mathbf{-log_{10}}\displaystyle\frac{\mathbf{-K_a+\sqrt{K_a^2+4yK_a}}}{\mathbf{2}}}
$$
問5 $${\underline{\mathbf{3.569}}}$$
(解説)
与えられた値を代入して解きます。
ルートの中身を計算すると$${\rm{\sqrt{3600\times10^{-10}}}=60\times10^{-5}}$$になるのがポイントでしょうか。
問題3
問1
(ア)、(イ): アミノ、カルボキシル (順不同)
(ウ): α-アミノ酸
(エ): ペプチド (トリペプチドでも可)
(解説)
(ウ): 詳細は以下のリンクに譲りますが、アミノ基とカルボキシル基が同一の炭素原子に結合していないものをβ-アミノ酸、γ-アミノ酸、… と言います。
αアミノ酸とβアミノ酸の違い
(エ): アミノ酸が数分子結合しただけだと、タンパク質とは呼びません。
本文では3分子しか結合していないので、タンパク質ではなくペプチドが適当です。
たんぱく質はアミノ酸が数十個以上つながってできていますが、ペプチドはアミノ酸が数個つながった状態のことをいいます。
問2
A: システイン
B: グリシン
C: グルタミン酸
(解説)
A: 硫黄反応が起きているので、S原子を含むシステインかメチオニンだと分かります。
グルタチオンの構造式を眺めてみると、下図の赤枠内にSH基(チオール基)をもつアミノ酸がありますね。これはシステインになります。(システインの側鎖は C-SH です。)
ちなみにメチオニンの側鎖は、C-C-S-C とS原子が炭素原子に挟まれた構造になっています。

C: 電気泳動より、小さなpH(=酸性)に等電点がありますね。
等電点が酸性なので、Cは酸性アミノ酸のアスパラギン酸かグルタミン酸のどちらかだと分かります。
そして、Aと同様に構造式を見ましょう。下図の赤枠内に、カルボキシル基が2個ついたアミノ酸がありますね。
こちらは側鎖が C-C-COOHとなっているのでグルタミン酸です。
(アスパラギン酸の側鎖は C-COOH です。)
ちなみに下図の青枠の通り、グルタチオンはグルタミン酸の側鎖がペプチド結合している珍しいタイプのペプチドです。

B: 最後に余ったグリシンとなります。
問3 下図参照

(解説)
グルタチオン2分子がジスルフィド結合しています。
還元剤としてはたらくのはSH基(チオール基)であり、Hを放出して自身は酸化されます。
問4 下図参照

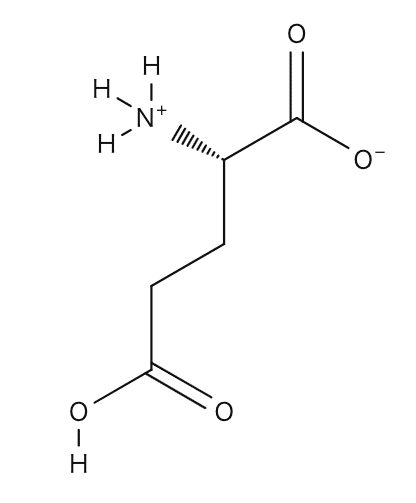
(解説)
「化合物が移動しなくなったpH」=等電点 ですから、
等電点における双性イオンの構造式を書けばよい、ということですね。
グルタミン酸側鎖のカルボキシル基は電離していないことに注意しましょう。
問5 24種類
(解説)
(構造異性体の組み合わせ) × (各構造における鏡像異性体の組み合わせ)になります。
構造異性体は3種アミノ酸の順列なので、3*2*1=6種類です。
(N末端から数えて)Glu-Cys-Gly, Glu-Gly-Cys, Cys-Glu-Gly, Cys-Gly-Glu, Gly-Glu-Cys, Gly-Cys-Glu の6種ですね。
また上記の各構造に対し、グルタミン酸とシステインはそれぞれ不斉炭素を持つので2*2=4種類の鏡像異性体を持ちます。
すなわち、6*4=24種類
問6 1.50g
(解説)
グルタミン酸と二酸化炭素の分子量はそれぞれ147と44。
またグルタミン酸1molの完全燃焼ではCO2が5mol生成する。
よって、$${\frac{1.0}{147}\times5\times44=1.4965…\simeq1.50}$$
「早く続きの解答作ってくれ〜🙏」という方がいらっしゃいましたら、
●この記事へのコメントや「スキ」
●twitterへのDM
などで教えてください!
すぐに無料で対応します👍
令和3年度の過去問解答
過去問はこちら
令和2年度の過去問解答
過去問はこちら
関連記事
準備中
