
【Excel】モンテカルロ法【RANDARRAY】
モンテカルロ法……正確な定義はググっていただくとして、ここでは「疑似乱数を使って近似値を求める手法」と理解いただければ問題ない。
直径1の円の面積をモンテカルロ法で求めてみよう。
疑似乱数によって円を内包する矩形内の座標を多数生成し、それぞれの座標が円の内側であった割合から、与えられる座標の取りうる範囲の面積に占める円の面積の割合を求めることができそうである。
円を内包する矩形だが、一辺の長さが1の正方形で問題ないだろう。

与えられる座標の取りうる範囲の面積に占める円の面積の割合を求めるつもりだったが、一辺の長さが1の正方形の面積は1である。よって、1に対する円の面積の割合は円の面積そのものとなる。
円とは平面上で中心から等しい距離にある点の集合である。
ある座標が円の内側であるならば、円の中心とその座標との距離が円の半径より小さい。
円の中心とその座標との距離を求めるのには三平方の定理を使うことができる。
a を 座標のx座標 - 円の中心のx座標 とする。
b を 座標のy座標 - 円の中心のy座標 とする。
c を 円の中心とその座標との距離 とする。

三平方の定理により、aの2乗 + bの2乗 = cの2乗 となる。
なお、円の中心を原点にすると、単に 座標のx座標の2乗 + 座標のy座標の2乗 で距離の2乗を求められる。

円の半径の内側であるということは、距離が半径よりも小さいことである。円の方程式と三平方の定理より、座標のx座標の2乗 + 座標のy座標の2乗 < 円の半径の2乗である。
前置きが長くなったが、ここまでわかればモンテカルロ法で計算することができる。
このような時に大量に疑似乱数を生成するのに使えるのがRANDARRAY関数だ。
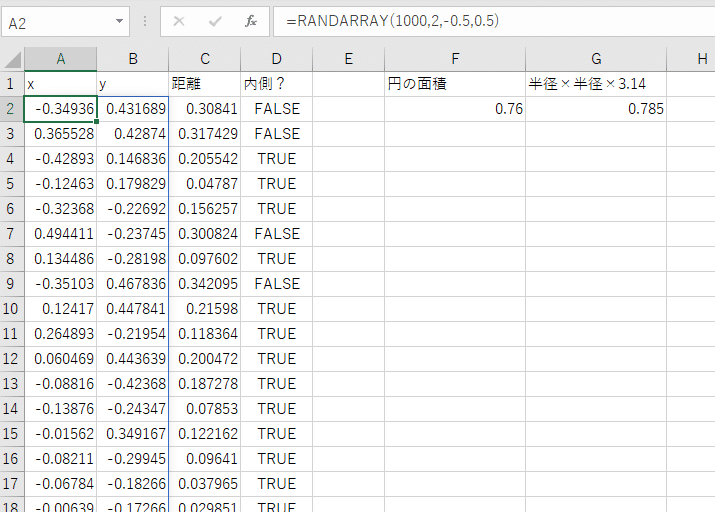
1行ごとに座標を生成(A列とB列)し、その座標の原点からの距離を求め(C列)、それが円の内側かを判定する(D列)。
そしてD列を集計し、円の内側と判断された割合が円の面積である(F列)。
念のため、円の面積の公式で求めた面積を隣(G列)に並べてみたが、ある程度一致した。
円周率の近似値として3.14を使用したが、円周率を返してくるPI関数を使った方がいいだろう。
