「ベルヌーイの定理」って言ってみたい

　航空機の設計に憧れていた私は、流体力学の授業が大学で始まったときに、ものすごいワクワクしてたんです（後にヒーヒーになりましたが）。

　なんか流体力学の授業で出てくる定理の名前が、すごくお洒落でカッコ良く感じたんです。

　「ベルヌーイの定理」とか「ナビエストークス方程式」とか、「レイノルズ数」とか。

　「流線形のデザイン」なんていうのも痺れますよね。

　ということで、飛行機の話

の蛇足で、ベルヌーイの定理について私が初歩で躓いたところを、振り返ってみたいと思います。

　飛行機の速度の測定には、「ピトー管」というものを使います。空調ダクト内の、風量測定なんかにも使われたりします。

　原理図は下図のようなものです。

[図1]ピトー管

　図1のように、一本の管内の液体表面に働く圧力の差を利用して、その面の高さから速度を算出します。

　ベルヌーイの定理は、

ρv^2/2（動圧）+ ρgh（重力圧） + P（静圧） = Const.（全圧） --- (1

で、これは流体の「単位体積あたりのエネルギー保存則」となっています。

　式1を"gh"で割れば、

v^2/2g（速度ヘッド）+ h（位置ヘッド） + P/ρg（圧力ヘッド）

= Const.（全ヘッド） --- (2

となり、位置ヘッドを無視すれば、

（全ヘッド）-（圧力ヘッド）=（速度ヘッド）

から「速度ヘッド」が分かります。

　言い換えると、

（全圧） - （静圧） = （動圧）

から「動圧」を算出し、大気の密度"ρ"を調べて、ピトー管に対する気体の速度を計算します。

　何故、図1の左の部分が「全圧」になるかというと、下の図2のように、運動する流体が物体と衝突する部分では、運動エネルギーが全て、圧力エネルギーに変換されるからです。

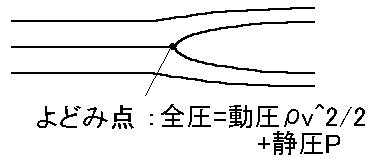
[図2]よどみ点(1)

　ピトー管の場合は、図2の「よどみ点」が管になっていますが、その管をたどった先の液面が、全圧を受けることになります。

　何故「よどみ点」なんていう名前が付いているかというと、ここで運動エネルギーが圧力に変換され、相対的に速度が"0"になる（つまり淀む）からです。

　この場合は、力学で言う「完全非弾性衝突」（衝突して運動エネルギを失う現象）にあたり、後に熱エネルギーとなります。

　とまあここまでは、参考書にも載ってる話なんですが、ここで私は以下のような疑問を持ちました。

「よどみ点では、

運動エネルギーが圧力エネルギーに変換されているだけ

なのに、なんで

静圧を含む全圧

になるのか？いったいこの場合の静圧とは何か？」

　ベルヌーイの式では、「流体の運動方向の圧力」が動圧で、「運動方向に垂直な方向の圧力」が静圧になると教わったからです。

　"Const."（定数）の部分の値が何なのか。これはエネルギーの観点から論じたものであり、具体的に何のエネルギーなのかははっきりしません。それを次回、見ていきたいと思います。