環境に超優しいエンジンの話

　そういえば、このシリーズは当初

「熱力学の歴史について書きます」

とか言っておきながら、前史だけでどんだけ時間かけるんだ

っていう感じでしたね。まあそれも楽しいんですが。

　科学技術の歴史の楽しさというのは、その知恵や技術を人間が得た、その当時の人々の思考をなぞれる事にあります。そしてそれを通じて、本筋で学んでいる科学技術のテーマを、より深く理解するのが大きな目的です。

　だから、そのテーマとなる内容も分からないと本当には楽しめないので、ここからお話しする熱力学の歴史も、その内容を深堀りしながら進めていこうと思います。（もっともらしい言い訳おわり。）

　ということで、やっと熱力学の話です。ちなみに前回の記事は

　1765年に、ワットがニューコメンの「蒸気力排水機」を改良して本格的な「蒸気機関」を発明してから、様々な蒸気エネルギを使った機械が開発されて行きました。つまり、

「熱を使って力学的な仕事を得る」

ということが、積極的に行われたわけです。

　そんな中で1824年、フランスのサディ・カルノーが「火の動力についての考察」を公刊します。この中でカルノーは、

「温度差が存在するところでは、必ず動力が発生する可能性があり、両熱源の温度差が大きいほど多くの動力が発生する」

という事を示しました。また、二つの「等温過程」と二つの「断熱過程」からなる「カルノーサイクル」を導入して、

「任意の可逆なサイクルの効率はカルノーサイクルの効率に等しく、可逆なサイクルが最大の熱効率"η"を持つ」

という「カルノーの定理」

η≦ (T[high] - T[low]) / T[high] = 1 - T[low] / T[high]

（等号は「可逆」のとき）

を示しました。（証明は本筋から外れますが、熱力学の議論の流儀が、式の変形の途中に詰まっているので、本文が終わった後に解説を試みます。）

　カルノーサイクルは、下図のように

「等温膨張」（図の1）→「断熱膨張」（2）→「等温圧縮」（3）→「断熱圧縮」（4）

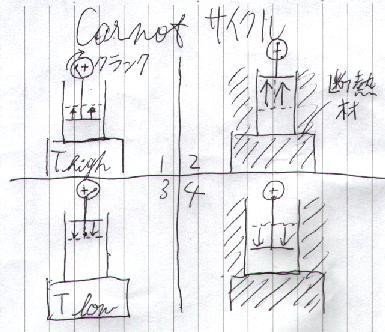
となっていて、このサイクルでは、(1) と (3) の「等温過程」で熱源と熱のやりとりをしている事になります。

　「熱のやりとり」というと、温度差があるものの間の熱の移動であるので、

「等温でどうやって熱を移動するんだ？」

と思うかもしれません。これは熱力学のもっとも難しいところの一つで、「準静的」に熱を移動させるわけです。そして、準静的であるときサイクルは「可逆」になるのです。

　具体的なイメージとしては、

ピストンをほんの少し引く
↓
ピストンの中が、熱源よりほんの少し、温度が低くなる
↓
熱源からほんの少しの熱が、ピストンに入る
↓
熱源とピストンが同じ温度になる

（下図）

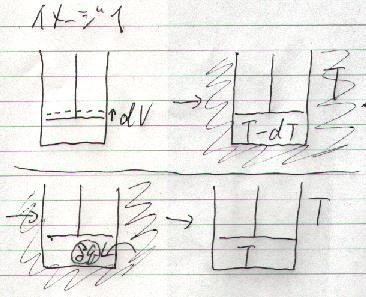
これを延々と繰り返します。

　「そんな事してたら日が暮れちゃうヨ！」

という声が聞こえてきそうですが、「日が暮れちゃう」どころか、1サイクル動かすのに丸々24時間かかるそうです。

　また、例えば水が大気圧下で沸騰する時、100℃という一定の温度で水から蒸気に変わる、つまり等温膨張します。このとき、熱源から受け取った熱は、「潜熱」として水蒸気に蓄えられますので、そのイメージでもいいと思います。

　これは、火力発電で利用されている「ランキンサイクル」という熱機関で利用されている過程です。ランキンサイクルはウイリアム・ランキンが1850年に考えた蒸気機関の一種です。

　またまた余談ですが、カルノーがこれを発表する前の1816年、ロバート・スターリングが「スターリングエンジン」の特許を取っています。

　このころは、ワットの発明した蒸気機関が主流でしたが、ボイラーの爆発事故が相次いて起こりました。そこで、「もっと安全な熱機関はないか？」として、「空気機関」であるこのエンジンが開発されたわけです。

　スターリングエンジンはカルノーエンジンよりも現実的で、実はカルノーサイクルと熱効率が同じなのです。しかし、小出力のわりに容積が大きいため、「内燃機関」の「オットーサイクル（ガソリンエンジン）」が1877年に開発されると、この機関はすたれてしまいました。

　しかし最近また、この熱源を選ばないスターリングエンジンが、環境汚染の緩和への期待から、見直されつつあります。スターリングエンジンについては魅せられている人も多く、多くのWebで紹介されているので是非見てみてください。

　ちなみに、カルノーエンジンやスターリングエンジンのように、外から熱をもらって作動する熱機関を「外燃機関」と呼びます。それに対し、ガソリンエンジンやディーゼルエンジンなど、シリンダの中で直接熱を生む（燃焼させる）熱機関を内燃機関と呼びます。

　外燃機関の方が内燃機関よりも、等温過程での熱のやり取りをする分、熱効率は高くなる傾向にあります。

　ところで、カルノーは熱素説論者であり、こんな事を言っています。それは、

「かくて動力の発生はカロリックの消費によってではなく、それの熱い物体から冷たい物体への移動によっておこると言わなければならない。」

　次回は、この「カロリック（熱素）」について、考察してみたいと思います。

■蛇足：カルノーの定理の証明

　まず熱効率"η"は、

外部にした仕事"W"

と

高温熱源から得た熱量"Q_H"

を使って、

η = W/Q_H

と表されます。ここで、熱機関が仕事をするには、後にお話しする「熱力学第二法則」より、

必ず低温熱源に熱"Q_H"を捨てる必要がある

という制約があります。

　そして、低温熱源に熱を捨てる以外に、

熱が逃げたり摩擦して熱が発生したりすることのない「全く損失の無いエンジン」

という理想のエンジンを考えると、「熱力学第一法則」から、

高温熱源でもらった熱"Q_H" = 外部にした仕事"W" + 低温熱源で捨てた熱"Q_L"

という関係が成り立つので、

W = Q_H - Q_L

として、熱効率を

η = (Q_H - Q_L)/Q_H = 1 - Q_L/Q_H

と書き直す事ができます。

　ところで、Q_HとQ_Lは、それぞれ熱源から「等温変容過程」（温度が一定で体積だけ変わる）で得た熱量であり、仕事の主体となっている気体を「理想気体」とすると、理想気体の状態方程式

PV = nRTから、

P = nRT/Vと変形して、

熱源との熱のやり取り＝等温過程での仕事

と考えてこれを「変化する体積"V"」を変数として積分すると、

∫PdV = ∫(nRT/V)dV = nRT lnV（lnは自然対数）

より、

高温熱源での体積変化：V1→V2

低温熱源での体積変化：V3→V4

として

Q_H = nRT_H ln(V2/V1）

Q_L = nRT_L ln(V4/V3)

と書くことができます。

　また、断熱過程では「ポアソンの関係式」から

TV^(γ-1) = const.（γは比熱比 Cp/Cv）

という関係があり、それぞれの断熱過程で

T_H V1^(γ-1) = T_L V4^(γ-1)

T_H V2^(γ-1) = T_L V3^(γ-1)

が成り立ち、

V1/V4 = V2/V3 = (T_L/T_H)^(1-γ)

より、

V1/V2 = V4/V3

となり、

η = 1 - Q_L/Q_H

から、

η = = 1 - T_L / T_H

となります。（証明おわり。）