
万華鏡の世界 ~平面充填とペンシルパズル~
-1.この記事は何か
この記事はペンシルパズルを知っている人向けに、平面充填についてパズルの視点でまとめたものです。平面充填・双対・ポリフォームに関連した英語版Wikipediaのページの解説を含んでいます。
0.自己紹介と雑談(読み飛ばし可)
panistaです。ペンパアドベント2018の17日目担当。あと1/4になってしまいました。
自分の2018年を振り返ると、世界大会にこそ参加しなかったものの、トケタに参加したり、オンラインコンテストを開いたりと色々活動してました。これまでで一番問題を作った一年だった気がします。
自分が初めて参加したパズルイベントが世界大会で、それから数年間ずっと競技パズルに参加しているので、競技パズルについて思うことが色々あります。
なんとなく競技パズルという言葉からは、ニコリでいうエキスパートタイムを競うようなイメージが浮かぶと思うんですが、それは競技パズルの全てではないと思います。むしろ自分が面白いと感じている要素は、オモロパズルに近いものです。
競技パズルでは、半分程度の大会で過去に出題例のないルール(大半は過去のルールのわずかな改変ですが)が出題されます。解き手は、過去に解いたルールの中から同じ考え方で解けるものを連想し、新しいルールに適用できる定理をその場その場ですばやく考える必要があります。
つまり、オモロパズルを早く解く力がかなりのウェイトを占めているんじゃないかなぁと思うわけです。(もちろんスリリンを早く解けることも重要ですけど)
で、オモロパズルと競技パズルの違いは何かというと、編集者がいるかどうかだと思います。競技パズルでは、出題するパズルを作者が自由に決められるので、どんなにひどいルールでも出題することができます。しかも、その問題を必ず解いてもらえるんです。作家からしたら、こんなにありがたいことはないんじゃないかと思います。その代わり、目の肥えた人たちが一斉に評価することになるので、下手な問題を出してしまうと自分の評判が落ちるという怖い側面もありますけど。
そんなわけで、競技パズルの大会はニコリと違って没が非常に少なく、作家の個性がそのまま強く出ることが特徴で、それが魅力の一つでもあります。今回の記事では、そんな個性派揃いの競技パズル作家の中でも特に奇妙なパズルを作っている、Dan Adamsという作家が作るパズルについて解説します。
長い記事ですが、他の人も気合が入った記事を書いているようですし、どうぞお付き合いください。ニコリやぱずぷれにあるような定番パズルのルールは知っている前提で書きます。
1.イントロダクション ~万華鏡~
さて、今回のタイトルは万華鏡の世界です。万華鏡。なんとなくクリスマスにマッチした、キレイなイメージがありますが、残念ながらここで語るのはパズルで生まれてしまった闇の概念についてです。最近、競技パズルの世界のなかでも一際目立つオンラインコンテストがLMIというサイトで開かれました。(LMIについては12/6のアドベントカレンダー参照 )
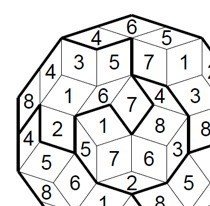
そのコンテストというのが、2016,2018年に開催されたKaleidoscopeです。この大会で出題された問題の一部を見てみましょう。左が全方向ヤジリン、右がクロットです。(例題。一部カット。解いてみたいという酔狂な人は、こちらへどうぞ。)

見てわかるように、この大会では、よくある正方格子の問題は一切出ません。代わりに出題されるのは、非常にいびつな形で構成された盤面。作者のDan Adamsは、この盤面を見て万華鏡(Kaleidoscope)とタイトルを付けました。そう言われるとそんな気もしてきます。
このような正方形ではない盤面を、変形盤面と呼びます。変形盤面自体は、競技パズルの世界では昔から度々出題されています。例えば、今年の10月にはTwitterで正六角形盤面のハニーアイランドコンテストが開催されましたし、2016年にはペンローズタイルばかりが出題されるラウンド (16th 24HPC Round4)が海外で開催されています。また、WPC(世界大会)でも変形盤面は毎年一問以上出題されます。それでも、これら大抵の変形盤面パズルは、通常のパズルの考え方を使えば解けるものがほとんどでした。
16th 24HPCで出題されたペンローズタイル数独(例題より)
しかしKaleidoscopeでは、全ての問題がこれまで出題されたことのないような複雑な形状をしています。しかもそのどれもが過去の問題と異なる考え方が必要なため非常にとっつきにくく、かつ高難易度の問題が揃っているため、界隈では有名なコンテストです。Kaleidoscopeで出題された盤面については、定理の解析はおろか、そもそも種類が多すぎて全容がまとまっていないのが現状です。
ということで、今回は、万華鏡(Kaleidoscope)の世界と題して、これら変形盤面の現状整理を目指します。具体的には、変形盤面にはどんな種類があり、どんなパズルを作れるのかを簡単にまとめます。
前半 2~4:英語版Wikipedia先生の力を借りた平面充填の話で、算数・数学っぽい内容です。
後半 5:実際にどんなパズルをつくれるのかという話です。
2.平面充填
さて、変形盤面をどう取り扱うかという話ですが、これは数学的には平面充填と呼ばれるものに相当します。平面充填とは、平面を決まった有限種類の図形で埋めつくすことを指す言葉です。例えば、一辺が1の正方形を使えば、平面を敷き詰めることができます。まずは、このような平面充填を分類しましょう。
(同様の内容のサイトは複数ありますが、全ての情報がまとまっているサイトが英語版wikiしか見つからなかったため、改めてここでまとめようと思います。)
それでは問題です。平面を図形で埋め尽くす方法は何通りあるでしょうか?
答えは当然無限です。正方格子を一列ごとに少しずらしてもいいですし、任意の一つの三角形を使えば平面を敷き詰めることができます。図形の一部を窪ませ、反対側を飛び出した形にしてもOK。なんだってやりたい放題です。さすがに自由度が高すぎるので、敷き詰める図形に制限を加えましょう。
平面を一辺の長さが1の正多角形を使って埋め尽くす方法は何通りあるでしょうか?ただし、辺の上に別の図形の頂点が来ないようにします。
答えを言う前に、制限がきつすぎて、一般論じゃないじゃないかと思った人に簡単に説明します。例えば、ニコリで出題された数少ない変形盤面パズル「たわむれんが」。正方形で敷き詰められていますが、辺の上に別の頂点がきています。

しかし、よく考えてみるとこの敷き詰めは正六角形盤面と同値です。あるマスに注目してみると、周りに6個のマスがありますが、これは正六角形の盤面でも同じことがいえます。このように、隣り合う図形が何かということに注目してみると、一見正多角形でないが、実は正多角形で置き換えられるという平面充填がほとんどで、今回の制限はそれほど強いものではありません。
過去出題されたことのある変形盤面のうち正多角形で表せないものというと、isometric cube、ペンローズタイル、フラクタル図形ぐらいでしょうか。他に、次の章で触れる「正多角形充填の双対」と同値なものがあります。(isometric cubeやペンローズタイルについては、類似した充填があるため、後述の考察に含まれています。)
Isometric-cube へやわけ (LMI: Magic Cube (2011) 例題)
(Isometric-cube … 立方体の等角図)

いくらでも変な敷き詰めは考えられるのですが、パズルの考察としてはひとまず十分な領域をカバーしていると思います。
さて、先程の問題の答えです。平面を正多角形でしきつめる方法は、なんと無限通りあります。これは困りました。とても整理ができそうにありません。しかし、無限種類の充填をきちんと分類する手法が考案されています。
それではどうするかですが、無限種類あるものを分類するためには、有限なものに着目します。今回の場合は頂点の形状です。例えば、正方形盤面の頂点は正方形(90度)が4つ集まってできています。このような内角の合計が360°になる正多角形の組み合わせは、以下の15通りしかありません。

注:
・頂点の周りを順に見た時、n角形がk枚連続することをn^kと表記します。
・この他に、平面充填に使用できないが頂点の角度の和が360度になる組み合わせが6通りあります。((3.7.42),(3.8.24),(3.9.18),(3.10.15),(4.5.20),(5^2.10))
・証明は、i番目に使用する図形をn_i角形として、内角(180°-360°/n_i)の和が360°になる整数の組をしらみつぶしします。平面充填で検索すれば出てくるので省略します。
無限通りある正多角形による充填ですが、その中身は以上にあげた15種類の頂点をどのように組み合わせるかということだけです。
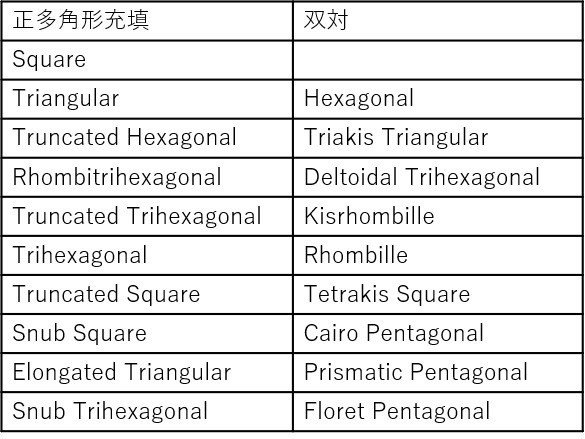
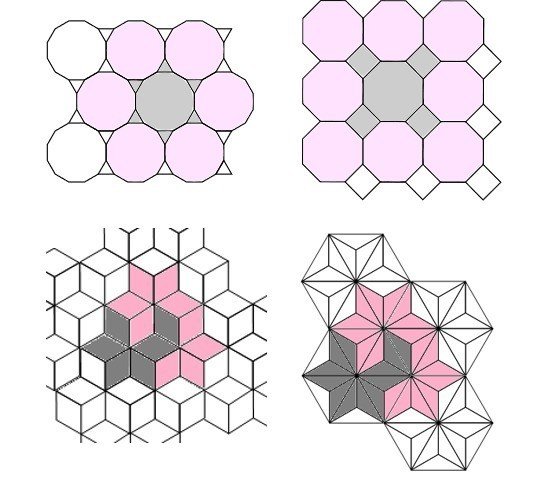
実際に敷き詰めてみるとこんな感じ。ここでは1種類の頂点形状からなる11種類の充填を列挙します。(なお、下図の中段下段に示している、「複数種類の正多角形を使い、かつ一種類の頂点形状だけが表れるように」充填した8種類の平面充填を、アルキメデスの平面充填と呼びます。)

名称ですが、Truncatedは対応する充填の「角をとった形」という意味でつけられています。SnubとElongated も数学的な図形操作の名称からとられているようです。
パズルでよく見かけるのは、Triangular,Hexagonal,Squareの3つですね。また、Rhombitrihexagonal, Truncated Trihexagonal, Truncated Squareの3つはKaleidoscopeで出題があります。あとは、Snub Squareのスリザーリンクをみた覚えがあります。
ここでは1種類の頂点からなる充填を図示しましたが、2~5種類の頂点形状からなる平面充填は英語版Wikipedia
Euclidean tilings by convex regular polygons
のk-uniform tilingsの項から閲覧可能です。
このページにおけるkは位置を含めて区別可能な頂点の種類、mは純粋な頂点形状の種類を表しています。この表によると、2種類の頂点からなる充填は20種類あります。また、k≧7の充填が何種類あるかは未解決問題のようです。
k≧2の充填についてはさすがにパズルでの出題例はないと言いたかったのですが、Kaleidoscopeで多数出題されており、
・Proximity Snake k=2,m=2,[3.4.6.4; 3^3.4^2]
・Sum Star k=2,m=2,[3.4.6.4; 3^2.4.3.4]
・Karst k=3,m=3,[3.4.6.4; 3.4^2.6; 4^4]
・Omni-Yajilin k=4,m=4,[3.3.4.3.4; 3^2.6^2; 3.4.4.6; 6^3]
・Kropki Switch k=5,m=4,[3.3.4.3.4; 3^2.6^2; (3.4.4.6)2; 4^4]
が使用されています。なんてこった。この作者、どう考えてもこの表を見ながらパズルを考案してます。

3.双対
平面充填には、双対という概念があります。多くの平面充填を取り扱ったサイトではおまけのように扱われていますが、パズルに関しては非常に重要な概念です。双対を理解するために、スリザーリンクを例に見てみましょう。
スリザーリンクは、辺に線を引くタイプの代表的なパズルです。例えば左の問題。ごく普通のスリザーリンクです。さて、このスリザーリンクを面に線を引くパズルに置き換えることはできるでしょうか。
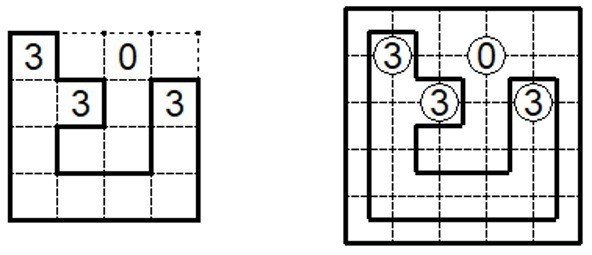
これは簡単で、右の図のようにすればよいです。両者は見た目が違うだけで同じパズルになります。 それでは、正六角形の盤面ではどうでしょうか。左のハニカムスリザーリンクを面に線を引くパズルとして置き換えることはできるでしょうか。少し考えると、正六角形の盤面のままでは難しいことがわかります。しかし、正三角形の盤面にすると、右の図のように置き換えることができます。

なぜ正三角形の盤面にすると、面のパズルに置き換えることができるのでしょうか。この性質を説明するのが、双対という概念です。
正六角形盤面の一つの頂点に注目します。一つの頂点には3つの正六角形が集まっていますが、この正六角形の中心を結ぶと、正三角形になります。このように、平面充填の中心を結ぶことによってできた新しい充填を、元の充填の双対と呼びます。この中心を結ぶという操作ですが、右図のように、面に線を引くことと辺に線を引くことを反転させています。

正六角形充填の双対が正三角形充填なので、ハニカムスリザーリンクは正三角形盤面に置き換えることができたわけです。また、正方形充填の双対は正方形充填なので、普段パズルを解くときには辺と面のパズルに本質的な差はありません。
というわけで、世の中には面で作るパズルと辺で作るパズルがあるので、分類のためには双対も考える必要があります。逆に、双対を含めてしまえば、全てのパズルを面のパズルとして考えることができます。それでは、さきほど挙げた頂点形状について、その双対を考えてみましょう。以下のようになります。

まあ何やら色んな形が出てきましたが、ここにあげた図形だけを組み合わせることで、正多角形充填の双対を形成することができます。正三角形充填の双対は正六角形充填、正方形充填の双対が正方形充填なのはスリザーリンクのところで述べた通りです。残りの単体で敷き詰め可能な8種類について、敷き詰めるとこんな感じになります。
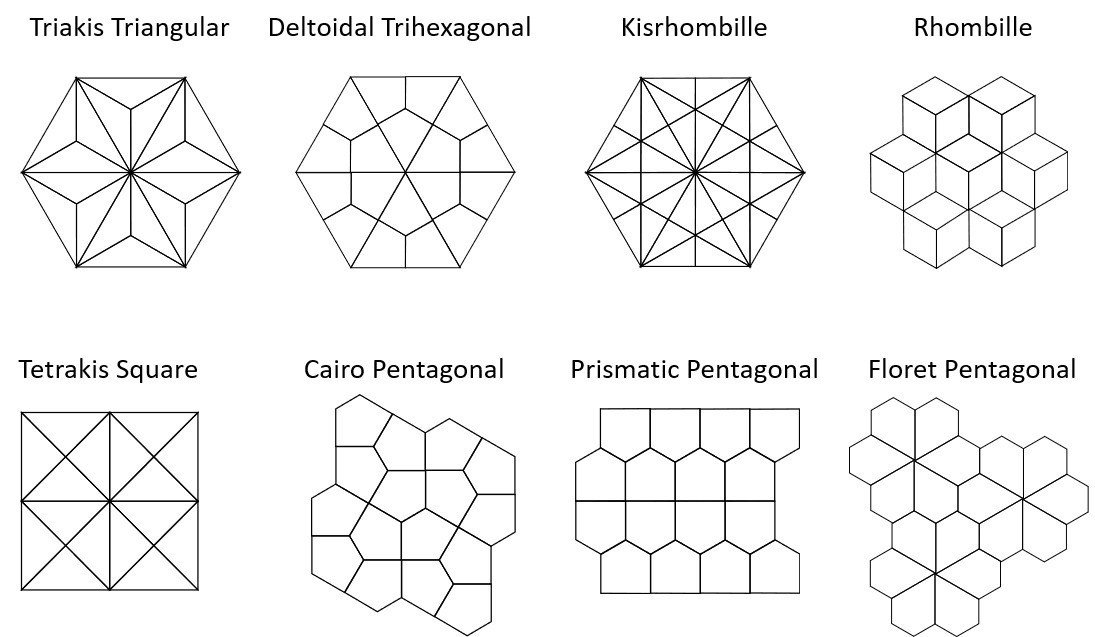
図形が一種類で扱いやすいためか、実はパズルの出題はこちらのほうが多いです。さすがに30°の三角形は使いにいのかTriakis TriangularとKisrhombilleは見たことがありませんが、あとの盤面はどれも複数回見たことがあります。Kaleidoscopeでは、Rhombille, Tetrakis Square, Cairo Pentagonalの出題がありました。ちなみに、Rhombilleの敷き詰め方を少し変えると、最初の方で触れたIsometric-cubeになります。また、すべてがひし形という点では、有名な非周期充填のペンローズタイルと類似しています。(ペンローズタイルはひし形を2種類使います。)
残念ながら、k-uniform tiling の双対がまとめられたサイトは見つかりませんでした。作図してみると、面白い性質をもった盤面が埋まっているかもしれません。Kaleidoscopeですらノータッチです。
4.平面充填の分類のまとめ
ということで、ここまで平面充填の分類をしてきました。

ここにあげた19種類の盤面について、パズルの適応可能性を探っていきます。(以下の章では、辺のパズルを全て双対における面のパズルに置き換えて考えています。)
今回は、ぱずぷれにあるパズルの一部を例に取り上げます。ぱずぷれにない種類のパズルでも、今回取り上げる考え方で分類できるパズルは多いはずです。
5 変形盤面とパズルルール
それではさっそく、変形盤面で適応できるルールを考えてみましょう。ここでは面白さや、盤面とパズルの相性は度外視です。とにかくルールが矛盾なく定義できればOKとします。
以下の文章では、変形盤面の名前がバンバン出てきます。覚えていないうちはなかなか読みにくいと思いますが、前節の充填の一覧図を手元に置くなどしてお読みください。
手始めに、ぱずぷれで一番最初に出てくるぬりかべを例に見てみましょう。
ぬりかべのルール(参考:ニコリ)
1.盤面のいくつかのマスを黒マスにする。
2.盤面の数字は、その数字が含まれる、黒マスによって分断された白マスの数を表す。
3.すべての白マスのカタマリに数字が1つ入る。数字のマスは白マスになる。
4.すべての黒マスはタテヨコひとつながりになる。
5.黒マスは2x2のカタマリになってはいけない。
これらを変形盤面でも定義できるかを考えます。
1.変形盤面でもマスはあるので、黒く塗ることはできます。
2.変形盤面でも区切られたマスが隣り合っているので、「白マスの数」という概念は存在します。
3.特に問題ありません。
4.ひとつながりも特に問題ありません。
5.2×2という概念は存在しません。一般的には、「ある頂点の周りのマスを全て黒マスにしてはいけない。」と読み替えることができます。
ということで、5番だけ読み替えれば、任意の盤面でぬりかべを作れます。
何も考えずに作ったRhombitrihexagonal ぬりかべ (作:panista)
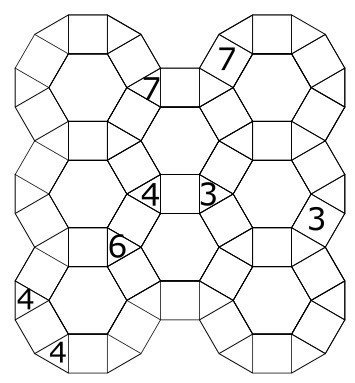
とまあ、実際に変形盤面にしても影響がないパズルはそこそこあります。
⓪そのまま適応できるルール
マスを黒く塗る。線を引く・ループを作る。マスがひとつながりになる。あるマスの周囲のマスを参照する。マスの面積を参照する。黒マスが2×2のカタマリにならない(「ある頂点の周りのマスが全て黒マスになってはいけない」と読み替え)。
つまり、ぬりかべ・のりのり・スリザーリンク・ナンバーリンク・フィルオミノ・クロット・月か太陽・tapaあたりは全盤面で作ることができます。彼らは殿堂入りです。好きな盤面で遊び散らかしてやってください。面白いかどうかは知りません。(きっと相性の良い盤面はあるはず。)
さて、残った数多くのパズルですが、残念ながら何かしらのルールが引っかかってしまいます。そこで改めて、パズルのルールを「変形盤面に適応できるかどうか」という視点でみてみると、いくつかのグループに分類することができます。
①直進or曲がる 例:ましゅ、スラローム
②列の概念 例:ヤジリン、美術館、へやわけ、カックロ、黒どこ、波及効果 他多数
②‘ラテンスクエア系(各行各列に、1から9の数字が一つずつ入るなどのルール) 例:数独、ABCプレース、Kropki、スターバトル
③白マスも黒マスも2x2のカタマリになってはいけない 例:しろまるくろまる、ぬりめいず
③‘全マス通過ループ
④ポリオミノ 例:LITS
⑤長方形の概念 例:シャカシャカ、四角に切れ、たすくえあ、チョコナ
⑥対称形 例:天体ショー、∀人∃HEYA
⑦重力 例:ドッスンフワリ
これら複数の要素を含むパズルもあります。例:さしがね①②
まだ個別ルールを加えると細かい分類はありますが、適用できるパズルが多い以上のルールを考察します。最後のまとめで、一覧表にします。
①直進or曲がる 例:ましゅ、スラローム
まずは分かりやすいところから、「直進」と「曲がる」という概念です。ましゅのキーとなる概念であるほか、非常に多くのループ系パズルで使われます。スラロームでは旗門を「直進」するという形で使われますし、パイプリンクなど交差のルールもこの概念に含まれます。正方形盤面では自明な概念ですが、変形盤面ではそうはいきません。
「直進」と「曲がる」が、どの変形盤面で破綻するかですが、敷き詰めに何角形が使われているかがポイントとなります。今回考えている多角形は、3,4,5,6,8,12角形の6種類ですので、それぞれについて考えます。

三角形を見てみましょう。下から入ると出口は2か所で、どう考えても直進できません。三角形が含まれていると、「直進」と「曲がる」が区別できないことが分かります。
四角形では、いびつな形でも対辺から抜けることを「直進」と定義すれば成立します。
五角形では、直進が2通り、曲がる方向がそれぞれ2通りあると考えることができます。定義は可能ですが、直進が2つに増えるため、パズルの解き味は悪くなってしまいそうです。適応可能性は△でしょう。パズルによってはうまくいくかもしれません。
六角形では、直進はそのままですが、曲がる角度が60度と120度の2種類に増えます。ほとんどの過去の出題では、120度を曲がると定義し、60度に曲がることを禁止しています。この定義だと正方形盤面と自由度が同じになるため、比較的自然に導入できます。
八角形と十二角形は、180度を直進、90度を曲がると定義することが自然でしょう。
というわけで、直進・曲がるを定義するには、三角形が含まれていなければOKです。五角形が含まれていると、定義は可能ですが中途半端なルールになるので、△とします。
ちょっと考えながら作ったDeltoidal Trihexagonal ましゅ (作:panista)
(直角の概念が謎なことになるので注意。)
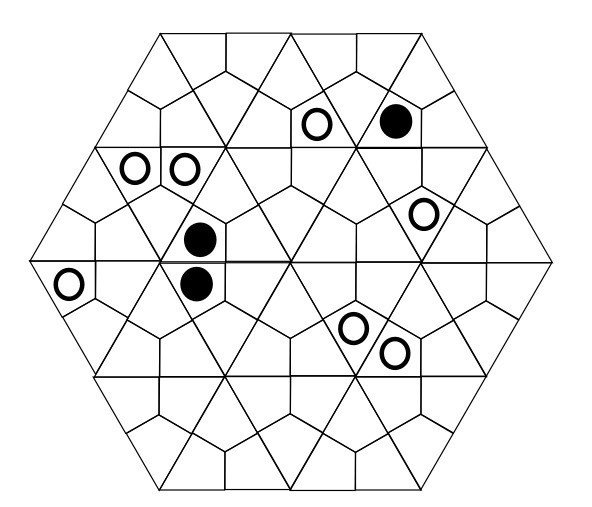
②列の概念 例:ヤジリン、美術館、へやわけ、カックロ、黒どこ、波及効果 他多数
変形盤面で破綻する代表的なルールが、列の概念です。列の概念は非常に多くのパズルで当たり前のように使われており、ヤジリンの矢印がさす方向、へやわけの三連禁、カックロの1つの和など、多種多様な形があります。正方形盤面では列と行は自明に定義できるため、普段はこれらのルールについて深く考えずに使っていると思いますが、変形盤面では多くの場合特殊な列が発生したり、列が定義できなかったりします。
列の概念の基本は、直進です。あるマスから直進し続けて盤面の端まで到達すれば、それが列となります。そのため、列が存在するかどうかも、直進と曲がる概念と同じように、敷き詰めに使用された図形が重要となります。
四角形、六角形、八角形、十二角形は直進が可能なので、列を作ることが可能です。
五角形では、直進が2通りあるので、列を定義できなくなり、破綻します。
残りは三角形ですが、これが非常にやっかいです。隣り合う図形によって、列の特性が変わります。正三角形の隣が四角形(八,十二角形も同様)だった場合、正三角形の方向にはもう直進ができないため、列が途中で途切れます。

その一方で、正三角形の隣が正三角形だった場合、上右図のように0°、120°、240°方向に3種類の列を定義することができます。また、正三角形の隣が正六角形だった場合、正六角形をbig cell(6枚の正三角形からなる大きな図形)とみなすことで、120°、240°方向に列を定義できる場合があります。ただし、正六角形が別の正六角形などに接していると定義が非常に複雑になって、実用的ではなくなります。そのほか、正三角形以外の三角形が隣り合っているとき、列の定義を決められる場合があります。列の例を下に示します。

三角形が存在すると、列が途切れる場合と途切れない場合、そもそも列が定義できない状況が起こります。ここで考えている列(ヤジリン、へやわけ、カックロなど)は途中で途切れても困らない列なので、破綻するのは五角形が含まれた盤面と、正三角形・直角二等辺三角形以外の三角形が含まれた盤面になります。TrihexagonalとSnub Squareは最長3マスの列しかなく、あまりに使いにくいため△とします。
※Deltoidal Trihexagonalでは、すべての列が12マスの円になるという非常に特殊な性質を持ちます。変なパズルを作れそうです。(Kaleidoscopeでは、Deltoidal Trihexagonalの双対であるRhombitrihexagonalで「ヤギとオオカミ」が出題されました。なかなか気持ち悪い仕上がりになっています。)
試しに作ってみたSnub Trihexagonal 美術館 (作:panista)
(3方向に光が伸びるので、制約が強すぎますね。)
12/18修正

②‘ラテンスクエア系(各行各列に、1から9の数字が一つずつ入るなどのルール) 例:数独、ビルディングパズル、ABCプレース、Kropki、スターバトル
②の拡張です。数独などでも列の概念を使用しますが、こちらは途中で途切れてはいけません。長さが3の列と9の列が混在していては、数独で大事な「1-9の数字が各行各列に存在」のルールが適用できません。このようなパズルには、数独を始めとする数字埋め系の他、スターバトルといったすべての行や列に同じ数のオブジェクトを置くパズルが該当します。このようなラテンスクエア系のパズルを成立させるためには、②に加えて、列が途切れる三角形が禁止になります。
※ビルディングパズルもラテンスクエアですが、「各行各列に1-Nの数字が表れる」を「各行各列に同じ数字が表れない」と読み替えることで、②に分類することが可能です。②‘のパズルは、多少ルールに手を加えることで②に分類可能な場合があるため、パズルと盤面ごとに慎重な議論が必要です。数独もうまくやると②にできるかもしれません。
③白マスも黒マスも2x2のカタマリになってはいけない 例:しろまるくろまる、ぬりめいず、ぬりみさき
「黒マスが2x2のカタマリになってはいけない」だったら、「ある頂点の周りのマスが全て黒マスになってはいけない」と読み替えればすべての盤面で適用ができたわけですが、「白マスも2x2のカタマリになってはいけない」というルールが加わると、問題が発生します。
「白マスも黒マスも2x2のカタマリになってはいけない。」というルールは、トケタvol.6などで取り上げられているように「外周にそった白マスと黒マスの切り替わりが2か所まで」という制約を発生させます。ところがTruncated Hexagonal では、外周に沿って3マス塗った瞬間に2x2禁に引っかかるため、パズルになりません。

というところまでは分かったものの、それ以上の統一的な説明が思いつきません。3つの図形が集まった頂点では必ず1:2に分けなければならないため、破綻しやすいかとも思ったのですが、正六角形盤面では苦しいながらもパズルとして成立するように思います。

何かうまい説明があるのでしょうか。今回はよくわかりませんでした。一応まとめでは、3つの図形が集まった頂点があると制約が強くなってしまうため、△とします。
少なくとも、Truncated Hexagonal とTriakis Triangular、Rhombille、Truncated Squareの4種では、ほとんど作成が不可能なようです。(小さい領域では作れるが、盤面を拡大できない。)
③‘全マス通過ループ
全マスを通過するループです。ニコリではほぼ使用されないルールですが、海外パズルでは頻繁に使用されます。(ヤジリンやリフレクトリンク、シンプルループは黒マスが入るため全通ループではありません。)
さて、なぜ③‘という番号が振られているかですが、「白マスも黒マスも2x2のカタマリになってはいけない。」というルールと深い関係があるためです。焼きもうふ氏のツイートを引用します。
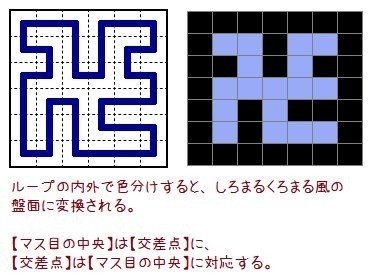
このように、全通ループは、しろまるくろまるの解答盤面で置き換えることができます。ここで注意することは、辺と面が入れ替わっていることです。変形盤面では、全通ループを双対のしろまるくろまるの盤面に置き換えることができます。
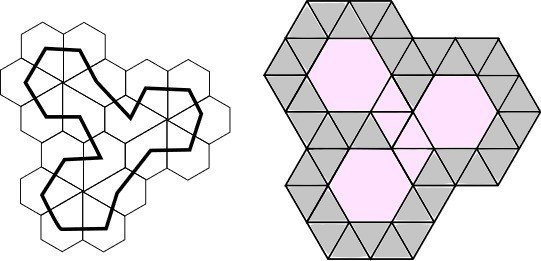
つまり、双対においてしろまるくろまるの盤面を作ることが困難な、
Truncated Hexagonal とTriakis Triangular、Trihexagonal 、Tetrakis Square
では全通ループが苦しくなることがわかります。
④ポリオミノ 例:LITS
もう一つ変形盤面で面白いルールが、ポリオミノの概念です。ポリオミノとは、正方形が複数枚集まってできた図形のことで、
1枚(1種類)をモノミノ
2枚(1種類)をドミノ
3枚(2種類)をトリミノ (IL)
4枚(5種類)をテトロミノ (LITSO)
5枚(12種類)をペントミノ (FILPNTUVWXYZ)
・・・
などと名前がついています。(Wikipedia ポリオミノ)
パズルでは非常によく用いられ、LITSではテトロミノが使われますし、ペントミノは海外パズルで好まれています。
正方形以外の図形を基準にしたポリオミノを一般にポリフォームと言い、たとえは正三角形ではポリイアモンド、正六角形ではポリへクスと言います。過去日本代表予選では、正三角形6枚からなるヘキサモンドの出題があります。またLITSの正六角形版のSLICYというパズルではテトラへクス7種(SLICYPO)のうち5種を使用します。
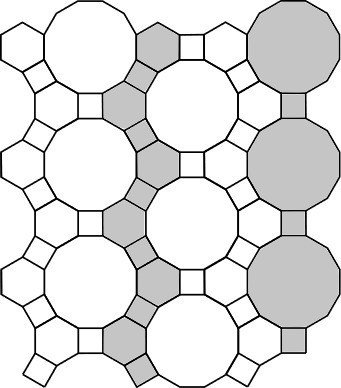
ということで、これが変形盤面に適応できるかという話です。充填が2種類以上の図形でできている場合もポリフォームの定義は可能かもしれませんが、種類が増えすぎてあまり面白くないでしょう。1種類の図形による充填に絞れば、それぞれの盤面でポリフォームを定義することができます。ここでは、Rhombilleを例に見てみましょう。

4枚は4種、5枚は12種でしょうか(自信ない)。数はポリオミノと大きく変わりませんし、変なパズルが生み出されそうな気配があります。
※ひし形を任意の向きで組み合わせたポリフォームをポリダイアモンドといいます。しかし、これはRhombilleに現れないもの(二つのひし形が同じ向きでつながるもの)を含んでおり、今回扱っているものとは別種です。変形盤面におけるポリフォームのポイントは、「平面充填に出現しない向きで接続してはいけない」という制約が付くところです。
※<雑学>
正三角形からなるポリフォームは、正三角形2枚の名前がダイアモンド(d+iamond)となるように、ポリイアモンド(poly+iamond)と名づけられました。モニアモンド、ダイアモンド、トリアモンド…となります。一方、ひし形からなるポリフォームは正三角形2枚、つまりダイアモンドが基準のため、ポリ+ダイアモンドと名付けられました。その結果、ひし形2枚からなる図形はダイダイアモンドとなります。ひどい名前。
参考(様々なポリフォームのまとめサイト)
1つの図形の持つ辺の種類が増えるとポリフォームの数は爆発的に増えるため、3種類の辺を持つpentagonal系は列挙が大変そうですが、ポリフォームの定義自体は問題ありません。(例えば、Cairo pentagonal のポリフォームであるポリカイロですが、トリカイロは3種類、テトラカイロは17種類あります。)ということで、一種類の図形からなる充填では、ポリオミノを使ったパズルを作ることができます。パズルの性質自体は、ポリフォームの数によって大きく変化しそうです。
⑤長方形の概念 例:シャカシャカ、四角に切れ、たすくえあ、チョコナ
⑥対称形 例:天体ショー、∀人∃HEYA
あとはおまけです。⑤の長方形ですが、明らかに変形盤面向きのルールではありません。Truncated squareは由来が正方形盤面のために長方形の定義が容易で、チョコナがKaleidoscopeで出題されました。また、正六角形盤面では、長方形をひし形と読み替えると四角に切れが作れます。他にも、正六角形盤面の中に本当の長方形を強引に作るシャカシャカがにしなんとか氏によって考案されました。いずれにしても、パズルのルールと平面充填を見比べながら、無理やり適応していったパズルになります。
⑥の対称形も、変形盤面ではかなり苦しいルールです。使用する図形が1種類かつ単体で対称形になっていないと、とてもパズルになりません。120度回転対称も対称形にすれば、Hexagonal, Triangle, Rhombusあたりで成立はするでしょうか。Hexagonal盤面のシンメトリーエリア(全ての領域が点対称になるフィルオミノ)はトケタで出題があります。
⑤も⑥も90度、180度という角度が非常に重要になるルールで、正方形盤面ならではのルールといえるかもしれません。その分、うまく変形盤面に適応できると楽しいのですが。
⑦重力 例:ドッスンフワリ
最後。重力の概念です。そもそも重力を使ったパズルが非常にレアですが、これも変形盤面には極めて相性の悪いルールです。重力が存在するためには、鉛直方向に列が存在する必要があります。Truncated Trihexagonal では下の図のように重力を定義できそうではありますが、パズルになるかというとどうなんでしょうか。あとは、上方向の枝分かれを認めるならHexagonalやTruncated Square、Elongated Triangular、Prismatic Pentagonalも候補になります。Hexagonal Aquarium(重力に従う水を、領域に入れていくパズル)は出題例があります。まだまだ可能性を秘めていそうなルールではありますが、そもそも正方形盤面でもっと成熟させろという話です。
6まとめ
以上、さまざまな変形盤面でどのパズルが使えるのか考察をしてきました。これを機に、変形盤面の考察が進んだり、変形盤面パズルが増えたりしたら楽しそうだなと思う次第です。あんまり増えすぎるとついていけないので、ほどほどにパズルの世界が広がりますように。
長文お疲れさまでした。各種ミスはご指摘ください。
最後にまとめの表です。充填の一覧図と合わせてご覧ください。辺のパズルについては、その双対の表を見てください。k-uniform tilingについても同様の基準で表が作れると思うので、誰も見たことのない変な盤面で作りたい人はぜひ()。

<参考文献>
・Kaleidoscope
http://logicmastersindia.com/2016/09P/
http://logicmastersindia.com/2018/10P/
・Kaleidoscopeの作者のサイトParamesis Puzzle Blog
http://puzzles.paramesis.com/
・Kaleidoscopeの作者が参加した、海外版オモパコンテストPIC2017。
Kaleidoscopeにも作者サイトにも出題のない変形盤面パズル7種(+通常盤面3種)が応募されています。
http://logicmastersindia.com/forum/forums/thread-view.asp?tid=1390&posts=16&start=1
Puzzle submissions compilationの記事のhereからダウンロード可能
・Wikipedia
https://en.wikipedia.org/wiki/Euclidean_tilings_by_convex_regular_polygons
https://en.wikipedia.org/wiki/Polyomino
・頂点形状の列挙やk-uniform tilingについて書かれた論文
https://web.archive.org/web/20150630004622/http://www2.math.uu.se/research/pub/Lenngren1.pdf
・k=1~7のk-Uniform tilingsの図を閲覧できるサイト(ランダム表示)
http://probabilitysports.com/tilings.html
・ポリフォームまとめサイト
https://dev.blueottergroup.com/Puzzles.html
