【Pythonで統計モデル】因子分析4：カテゴリカル因子分析

2023年4月27日 08:49

はじめに

株式会社GA technologiesの福中です。今、僕は、Advanced Innovation Strategy Center（以下AISC）という部署でChief Data Scientistとして働いています（詳しい自己紹介はAISC WEBサイトのプロフィールをご覧ください）。前回に引き続き、【Pythonで統計モデル】というシリーズの記事を書いていこうと思います。前回は尺度構成を行う際の因子分析を、Pythonを使って実行する方法について解説しました。

第4回目である今回は、変数に順序カテゴリカルデータが含まれる場合の因子分析、すなわちカテゴリカル因子分析もPythonで実行可能であることを確認していきます。

注意点

本記事は統計学およびPythonの初心者向け解説記事ではありません。普段からR等を使って統計モデルによる分析や研究を行っている研究者の方が、改めてPythonで因子分析を行う必要が出た際のリファレンスとしての利用を想定しています。したがって、因子分析に不慣れな方は、先に以下で紹介するテキストをはじめとした初心者用の教科書で勉強するとよいと思います。

テキスト

本記事では東京図書から出版されている因子分析入門―Ｒで学ぶ最新データ解析―の分析結果を、Pythonを使って再現していきます。分析用データは東京図書のホームページからダウンロードできますので、興味のある方はぜひ試してみてください。

環境

本記事の分析は、OS: Windows 11、Python 3.11.2の環境下で行っています。また、必要なパッケージは以下となります。インストール済みの方は割愛してください。

# packageのインストール

pip install numpy pandas matplotlib japanize_matplotlib
pip install factor_analyzer
pip install semopy

なおPythonにおける因子分析のパッケージであるfactor_analyzerのドキュメントは以下となります。

またsemopyは構造方程式モデリング（Structural Equation Modeling: SEM ）を行うためのパッケージで、ドキュメントは以下にあります。

本記事ではここから重要な部分をいくつかピックアップしてご紹介します。網羅的な解説はしませんので、適宜、必要に応じてご参照ください。

カテゴリカル因子分析の概要

一般的に因子分析というと、観測変数はすべて連続量であることを前提としています。尺度構成のように、自分で作成した質問紙を使って自らデータを取得できる場合には、この前提は問題にはなりません。しかし、実際のデータには何らかの理由で順序カテゴリカルなデータとして取得されたものも多く、この場合にも因子分析を行いたいというシチュエーションも発生します。このような連続量と離散量が混在したデータセットに対して実行できる因子分析をカテゴリカル因子分析といいます。

それでは、なぜカテゴリカルデータを連続量と同等に因子分析してはいけないのでしょうか？一般的に3件法などで測定された質問紙調査のデータは、その背後に連続量を仮定し、何らかの閾値で切断された結果として得られたものと考えます。そしてその連続量の切断の結果として得られたカテゴリカルデータを使って相関係数を求めると、連続量同士の相関係数よりも一般的な傾向としてその絶対値が小さくなります。これも一種の希薄化と言えるでしょう。そして、因子分析をはじめとした多変量解析は変数間の関係性の分析、すなわち相関関係の分析といえるので、希薄化が起こってしまい相関係数が小さくなってしまえば、その分析結果は正しいものにはなりません。ゆえに何らかの対処をする「希薄化の修正」が必要になってくるのです。

Mplusのような専門のソフトウェアであれば、変数を明示的にカテゴリカルデータとして指定することで通常の因子分析と同等に分析可能なのですが、Pythonを使って探索的因子分析を行う場合には何らかの工夫が必要になります。その工夫の1つが質的相関係数を求めて、その相関行列に対して因子分析を行うというものです。質的相関係数を求めることによって相関係数の希薄化を修正しようということです。factor_analyzerを利用する際、これまでは分析対象のデータを素データとして読み込んできましたが、ある引数を指定することで、相関行列をそのままデータとして読み込み、分析を行うことができるようになります。今回の記事ではこの方法を見ていきましょう。

相関係数の種類

一般的に相関係数というと以下の式を思い浮かべると思います。

$$
r = \frac{\text{Cov}(x, y)}{s_xs_y}
$$

ここで$${\text{Cov}(x, y)}$$は変数$${x}$$と変数$${y}$$の共分散、$${s_x}$$は変数$${x}$$の標準偏差、$${s_y}$$は変数$${y}$$の標準偏差を表しています。これをピアソンの積率相関係数といい、単に相関係数というと暗黙のうちに上記の相関係数を想定していることがほとんどだと思います。

しかし、繰り返しになりますが、このピアソンの積率相関係数は両変数が連続量のときにのみ使用するのが望ましいです。どちらかの変数がカテゴリカルである場合は、希薄化が起こり、絶対値が小さく推定されてしまいます。実は相関係数には、ピアソンの積率相関以外にもいくつかの種類が存在します。

テトラコリック相関係数：2つの変数ともにカテゴリカル変数であるが、両変数ともにカテゴリ数が2である場合
ポリコリック相関係数：2つの変数ともにカテゴリカル変数であるが、少なくとも一方の変数のカテゴリ数が3以上である場合
バイシリアル相関係数：2つの変数のうち一方が連続変数、もう一方がカテゴリカル変数でかつそのカテゴリ数が２である場合
ポリシリアル相関係数：2つの変数のうち一方が連続変数、もう一方がカテゴリカル変数でかつそのカテゴリ数が3以上である場合

相関係数を求める際には、扱う変数の種類によって、上記4つの質的相関係数と積率相関係数を使い分けるように注意しましょう。ただし、上記で紹介した質的相関係数は、その背後に仮定する連続量が正規分布に従っていることを前提にしたパラメトリックな推定方法です。変数の値が完全な順位になっている場合などには、順位相関のようなノンパラメトリックな相関係数を求めるようにしましょう。

質的相関係数を求めてみよう

それではまずデータの読み込みから始めましょう。今回利用するデータは、テキスト第3章で使用されている「6科目学力データ（質的）」になります。このデータはシミュレーションによってつくられた人工データで、「英語」「現代文」「古典」「数学」「物理」「地学」の試験結果として想定されています。試験はすべて100点満点で採点されていますが、ここでは「現代文」と「物理」については40点未満を1、40点以上60点未満を2、60点以上を3にカテゴライズされてあります。また、「古典」と「地学」に関しては60点未満を1、60点以上を2にカテゴライズされています。したがって、「英語」と「数学」が連続変数、「現代文」「古典」「物理」「地学」がカテゴリカル変数になります。

# packageの読み込み

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import semopy
from factor_analyzer import FactorAnalyzer

# 6科目学力データ（質的）の読み込み

data_disc = pd.read_csv("dat/6科目学力(質的).csv", encoding='shift_jis')
names = data_disc.columns
data_disc.head()

次にこのデータからカテゴリカル因子分析をやりたいところですが、factor_analyzerでは、変数を直接カテゴリカルデータとして指定することができません。そこで当初の予定通り、質的相関係数を求めましょう。

しかし、残念ながらfactor_analyzerには質的相関係数を求めるためのメソッドは準備されていません。「Pythonではできないのかな？」と思っていたのですが、質的相関係数はよく構造方程式モデリング（SEM）の枠組みで解説されることが多く、「もしかしたらSEMのパッケージ（semopy）の中にあるのではないか？」と思い、semopyのドキュメントの中を探してみました。

すると、Sub-modulesの中にsemopy.polycorrというものがあり、hetcorというメソッドを見つけました！説明にも

Compute a heterogenous correlation matrix.

公式ドキュメント

と書いてあり、「まさにこれで計算できそうだな！」と思ったのですが、実際にはうまく動きませんでした笑
いろいろ試してみた結果、2023年3月現在では、hetcorはsemopy.modelの中に移動されたみたいで、以下のように記述すると質的相関係数が算出できました。どうやら公式ドキュメントの更新が止まっているだけのようでした。

# 質的相関係数を求める（2023年3月3日には動かなくなっていた）

cormt_disc = semopy.model.hetcor(data_disc)
print(cormt_disc)

さて、上記のスクリプトで2023年2月28日までは確かに質的相関係数が計算できていました。しかし、この記事を書いている2023年3月3日に再度計算してみると、急にエラーが出るようになってしまいました。つい先日まで動いていたスクリプトが急に動かなくなったので、最初はとても混乱しました。おそらく内部で依存関係にある何かのパッケージをアップデートしてしまったため、このような事態になったのでしょう。

何とか解決しようと頑張ったのですが、うまくいかず途方に暮れていたので、AISCメンバーの丸山さんに相談しました。丸山さんは2021年4月入社の新卒3年目の自然言語処理を専門としている若手メンバーで、開発方面の知識が豊富でプログラミングを得意としている方です。その丸山さんに相談したところ、どうやらsemopyの中のpandasが悪さをしているらしく、pandasのデータフレームからnumpy配列に変換してからやればうまく動くことを発見してくれました。そこで、上記のスクリプトを以下のように修正します。

# 質的相関係数を求める

tmp = semopy.model.hetcor(data_disc.to_numpy(), nearest=True)
cormt_disc = pd.DataFrame(tmp, columns=names, index=names)
print(cormt_disc)

           英語     現代文      古典      数学       物理      地学
英語    1.000000  0.815372  0.772376  0.444761  0.446339  0.430621
現代文  0.815372  1.000000  0.804314  0.410427  0.402097  0.474632
古典    0.772376  0.804314  1.000000  0.388621  0.359759  0.320938
数学    0.444761  0.410427  0.388621  1.000000  0.785459  0.704937
物理    0.446339  0.402097  0.359759  0.785459  1.000000  0.680073
地学    0.430621  0.474632  0.320938  0.704937  0.680073  1.000000

すると今度は問題なく質的相関係数を算出することができました。値もテキストP.76の表3.4とおおむね一致していることがわかります。ここで1点注意があります。ポリコリック相関係数をはじめとしたカテゴリカル変数を扱った相関係数の計算式には積分が含まれます。積分計算の近似法にはいくつかのやり方があるので、質的相関係数の推定結果にはソフトウェアごとで少し異なる場合があります。今回のようにテキストの結果と多少（小数点第2位の精度）のズレが起こったのはそのためだと考えられますが、大きな差異ではないのでそれほど問題になることはないでしょう。

カテゴリカル因子分析の実行

後は、これまで通り通常の因子分析を行えば求める推定結果が得られます。ただし、データを読み込むための引数を相関行列にしておく必要があります。具体的には以下のように"is_corr_matrix=True"のようにします。

# カテゴリカル因子分析の実行

fa = FactorAnalyzer(n_factors=2, rotation='promax', method='ml', is_corr_matrix=True)
fa.fit(cormt_disc)

スクリーテストの結果は以下の通りです。テキストと同様に因子数を2とするのが良さそうということがわかります。

# スクリーテスト

eigen = fa.get_eigenvalues()
left = list(range(1, len(eigen[0])+1))
plt.plot(left, eigen[0], marker="o")
plt.ylabel("固有値")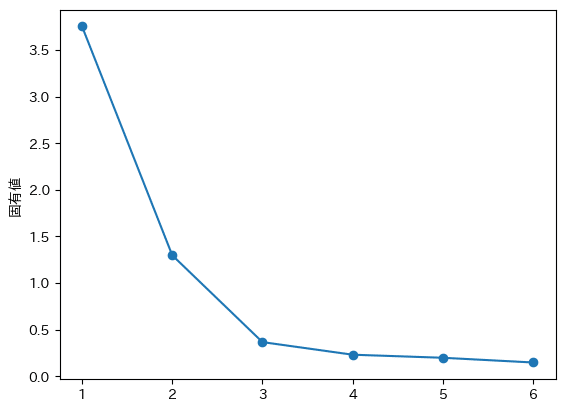

因子負荷量を出力すると以下のようになりました。

loadings_df = pd.DataFrame(fa.loadings_, columns=["第1因子", "第2因子"])
loadings_df.index = data_disc.columns
print(loadings_df)

        第1因子    第2因子
英語    0.848025  0.068298
現代文  0.923032  0.002618
古典    0.894286 -0.044291
数学   -0.028978  0.914087
物理   -0.026526  0.886569
地学    0.067452  0.748935

ここで、比較のためにカテゴリカルデータを連続量とみなして、通常の因子分析を実行した結果も見てみましょう。

# カテゴリカルデータに対して通常の因子分析を行った場合

fa = FactorAnalyzer(n_factors=2, rotation='promax', method='ml')
fa.fit(data_disc)

loadings_df = pd.DataFrame(fa.loadings_, columns=["第1因子", "第2因子"])
loadings_df.index = data_disc.columns
print(loadings_df)

        第1因子    第2因子
英語    0.824598  0.082347
現代文  0.852844 -0.014112
古典    0.658852 -0.029950
数学   -0.030773  0.908617
物理   -0.027054  0.807657
地学    0.053164  0.546948

このようにもともと連続量である英語と数学では因子負荷量にそれほど差異はありませんが、カテゴリカルデータである現代文・古典・物理・地学ではカテゴリカル因子分析を行った方がかなり高く推定されていることがわかります。これはカテゴリカル因子分析を行うことによって相関係数の希薄化が修正された結果と言えるでしょう。

最後に

このように変数にカテゴリカルデータを含む場合であっても、Pythonで正しく因子分析を行えることがわかりました。これで探索的因子分析を行う際にはPythonは不足のないツールであることが確認できました。次回はいよいよ確認的因子分析をPythonで行う方法を見ていきます。

因子分析5へ続く

この記事が気に入ったらサポートをしてみませんか？