
文系出身の営業人材がデータサイエンティストの一歩目を踏み出してみた
はじめに
もともとデータ分析とは無縁な人生を歩んできた私ですが、ひょんな出会いから機械学習サービスを開発する会社に入社をし、「機械学習とかデータ分析なんても何も知りまてん❤️」とは口が裂けても言えない環境の中で焦りまくっていた矢先、たぶん何かの広告でAidemyの超魅力的なキャッチコピー(初心者でも機械学習をマスターできる!みたいな)に釣られ「データ分析講座」を受講するに至りました。
こうして受講終了が見えたタイミングで考えてみると、あの時私を釣っていただいて本当に良かったなと感謝しています。Aidemyのマーケティング担当の方ありがとうございます(笑)
さてこのブログ記事ですが、Aidemyのカリキュラムの一環で、受講修了条件を満たすために執筆、公開をするものですので、内容については大目に見ていただけると嬉しいです。
(「はじめに」がめちゃくちゃ長くなっていますが、たぶん大事なはずなのできちんと書きます!!)
で、例に漏れずブログテーマにはすごく悩んだのですが、元々学生時代に陸上競技をやっていたこともあり、マラソンをテーマとするものに決めました。やはり馴染みのあるテーマを選ぶって大事ですね。分析がめちゃくちゃ楽しかった。
記事の内容
どんな人に読んで欲しいか
機械学習とは現時点で無縁だけど何か新しいスキルを身につけたいと思っている文系出身者
この記事に書くこと、わかること
Aidemyの講座を受講すると身につけられる分析スキル
この記事で扱わないこと
難しい分析やコーディング
私自身もデータ分析を勉強し始めて半年くらいの身ですので、あまり難しい分析やコーディングはできません。
あくまで同じようなバックグラウンドを持っていて、何か新しいスキルを身につけたいと思っている方にぜひ読んでいただきたいです。現時点ではきっとよくわからない単語がたくさん出てくると思うのですが、6ヶ月後にはなるほどね、と言っている自分がきっといるはずです。
データについて
今回はこちらのサイトよりデータを拝借させていただきました。
数値データとカテゴリカルデータが混在するデータセットとなっており、それらの違いを踏まえて取り扱わなければいけない点が難しかったです。
取得背景
マラソン愛好家が好む時計(Garminなど)で取得できるトレーニング歴やペース配分と実際の結果をリンクさせることで、生化学的な視点からではなく、ある種の非正統的な観点からタイムに効く因子を導き出そうとして取得されたデータ
パラメータ
ID:いわゆるID
Marathon:マラソン名
Name:ランナーの名前
Category:ランナーの性別と年齢グループ
MAM:男性/40歳未満
WAM:女性/40歳未満
M40:男性/40歳から45歳
km4week:直前4週間で走った総距離
sp4week:直前4週間のトレーニングにおける平均速度
cross training:サイクリストまたはトライアスリートであるか
Wall21:(よくわからん…おそらく前半タイムと後半タイムの比)
Marathon time:マラソンを走り終えた時のタイム
CATEGORY:マラソンタイムごとのグループ
A:3時間未満の結果
B:3時間から3時間20分の間の結果
C:3時間20分から3時間40分の間の結果
D:3時間40分から4時間の間の結果
分析の流れ
以下の流れで分析を進めていきたいと思います。
データの準備
データクレンジング
データの可視化
ベースモデルの作成
モデルの改善
特徴量重要度、SHAPの確認
いざ分析開始
データの準備
ライブラリとデータをまずは読み込みます。
# ライブラリ等のインストール
!pip install japanize-matplotlib
!pip install shap
import pandas as pd
import numpy as np
import japanize_matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import KFold
# データの読み込み
df = pd.read_csv("/content/MarathonData.csv", encoding='utf-8')そして、データの概要をチェック。
# データの概要を確認
def df_stats(data):
print(" 【SHAPE】")
print("ROWS: {}".format(data.shape[0]))
print("COLUMNS: {}".format(len(df.columns)))
print()
print("【TYPES】")
print(data.dtypes)
print()
print("【MISSING VALUES】")
print(data.isnull().sum())
print()
print("【DUPLICATED VALUES】")
print("NUMBER OF DUPLICATED VALUES: {}".format(data.duplicated().sum()))
df_stats(df)出力結果は以下の通り。

一部の特徴量にてデータ型の修正が必要なのと、欠損には適切に対応しないと使用できるデータがなくなってしまいそう。
加えて、データ数に対して特徴量が多めなので、特徴量選択は重要になると見立て。
ということで、早速データクレンジングを実施。
データクレンジング
まずはデータ型の修正から。
# idをオブジェクト型に変更
df['id'] = df['id'].astype('object')
print("Data type of 'Wall21' after conversion:", df['id'].dtype)
# Wall21に含まれる「-」を「NaN」に置換した上で、float型に変更
df['Wall21'] = df['Wall21'].replace(' - ', pd.NA)
df['Wall21'] = pd.to_numeric(df['Wall21'], errors='coerce')続いて、欠損の対応を実施。
# CrossTrainingカラムの欠損に「nonct」を代入
df["CrossTraining"].fillna("nonct", inplace=True)
# 欠損の削除
df.dropna(inplace=True)最後に外れ値を削除(これが大変だった…)。
# 数値データを抽出
categorical_variables = df.select_dtypes(include=['object', 'category']).columns
data_df = df.drop(columns=categorical_variables)
# 外れ値を検出し、それらを含む行を表示する関数
def detect_outliers(df):
# 各行に対して外れ値を含む変数名を格納するためのリストを初期化
outliers_in_row = []
for i in range(df.shape[0]):
outlier_variables = [] # 現在の行における外れ値の変数名を格納
for column in df.columns:
# 外れ値の基準を計算
Q1 = df[column].quantile(0.25)
Q3 = df[column].quantile(0.75)
IQR = Q3 - Q1
# 現在の行が外れ値かどうかを判定
if df.iloc[i][column] < Q1 - 1.5 * IQR or df.iloc[i][column] > Q3 + 1.5 * IQR:
outlier_variables.append(column)
# 現在の行に対する外れ値の変数名をリストに追加
outliers_in_row.append(outlier_variables)
# 新しいカラムとして外れ値の変数名を格納
df['outlier_variables'] = outliers_in_row
return df
# 各変数ごとにサブプロットを作成して箱ひげ図を描画
fig, axes = plt.subplots(nrows=1, ncols=data_df.shape[1], figsize=(18, 6), sharey=False) # sharey=Falseで各サブプロットに独立した縦軸を設定
for ax, (col_name, data) in zip(axes, data_df.items()):
sns.boxplot(data=data_df[col_name], ax=ax, orient="v", palette="Set3")
ax.set_title(col_name)
ax.grid(True)
plt.tight_layout()
plt.show()
# 外れ値を含む行を表示
outlier_df = detect_outliers(data_df)
outlier_df = outlier_df[outlier_df['outlier_variables'].map(len) > 0]
outlier_df外れ値を確認するとkm4weekとsp4weekにて計7つありそう。

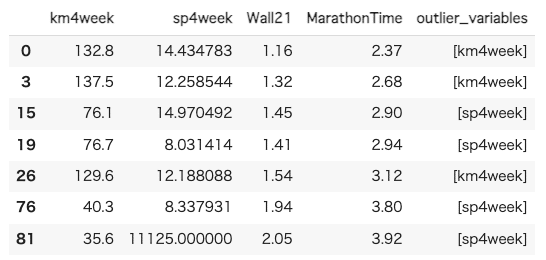
ということで7つのデータを削除
df = df[(df["km4week"] < 129.6) & (df["sp4week"] < 14.9) & (df["sp4week"] > 8.34)].reset_index(drop=True)クレンジング後のデータの形状は以下の通り。
【SHAPE_after_cleansing】
ROWS:74
COLUMNS:10
さらに元長距離ランナーのドメイン知識を用いてマラソンタイムに影響しない特徴量も削除(とはいっても誰でもわかる処理だけど)。
df.drop(columns=["id", "Marathon", "Name", "CATEGORY"], inplace=True)最終的なデータの形状は以下の通りで、これならモデルも作れそう。【conclusive_df_SHAPE】
ROWS:74
COLUMNS:6
データの可視化
データの前処理が完了したので、次は基礎分析へ。
まずは数値データとカテゴリカルデータごとにマラソンタイムとの相関性を可視化。
# 数値型のデータのみを抽出
numeric_df = df.select_dtypes(include=[np.number])
# 相関係数行列を計算
corr_matrix = numeric_df.corr()
# ヒートマップで相関係数行列を表示
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('Correlation Matrix')
plt.show()
km4week、sp4week、Wall21ともにマラソンタイムとの相関を確認。特にWall21とは非常に強い正の相関があるとのこと。
続いてカテゴリカルデータとマラソンタイムとの関連性を可視化。
def plot_category_time(data, x, y):
f, ax = plt.subplots(figsize=(10, 3))
sns.swarmplot(data=data, x=x, y=y, ax=ax)
plt.title("Marathon / Time")
plt.xlabel(x)
plt.ylabel(y)
plt.show()
# CrossTrainingとMarathonTimeの散布図
plot_category_time(df, "CrossTraining", "MarathonTime")
# CategoryとMarathonTimeの散布図
plot_category_time(df, "Category", "MarathonTime")結果は以下の通り。
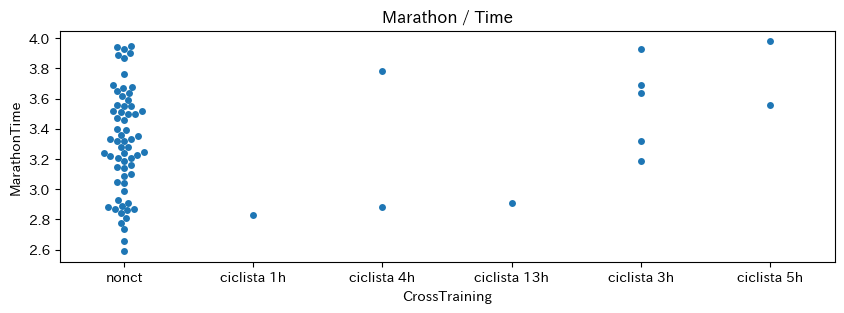

これといった強い関連性はなさそう。ある程度数値データでマラソンタイムを予測できるかも。
ベースモデルの作成
ということでここからはベースモデルの作成に取り掛かる。
まずは変数選択から。カテゴリカル変数にOne-Hotエンコーディングを施す。
df = pd.get_dummies(df, dtype=int)改めてマラソンタイムと各特徴量の相関関係を確認。
df.corr().abs()["MarathonTime"].sort_values(ascending=False)結果は以下の通りで、Categoryはあまりマラソンタイムに効いてなさそうなので、説明変数からは除こう。

最後に目的変数(y)と説明変数(X)を設定。
X = df[df.columns[list(range(0, 3)) + list(range(10, df.shape[1]))]]
y = df["MarathonTime"]続いてデータを訓練用データとテスト用データに分割。
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.2, random_state=42)そしていよいよベースモデルを構築し評価!アルゴリズムはシンプルに線形回帰を使用して様子見。
# 線形回帰モデルの初期化
model_0 = LinearRegression()
# モデルの学習
model_0.fit(train_X, train_y)
# 予測
pred_0 = model_0.predict(test_X)
# 決定係数
r2_0 = r2_score(test_y, pred_0)
print("R^2 Score(base model):", r2_0)決定係数は0.93とのこと。ちょっと過学習気味か…。
モデルの改善
少し工夫もしてみたいと思う。
まずはクロスバリデーションを実施。
# K-Foldを定義
cv = KFold(n_splits=4, random_state=42, shuffle=True)
# YYプロットと決定係数計算用のリスト作成
true_vals_1 = []
pred_vals_1 = []
r2_scores_1 = []
# 線形回帰モデルの初期化
model_1 = LinearRegression()
# クロスバリデーションを実施
for train_index, test_index in cv.split(X):
train_X, test_X = X.iloc[train_index], X.iloc[test_index]
train_y, test_y = y.iloc[train_index], y.iloc[test_index]
# モデルの学習
model_1.fit(train_X, train_y)
# 予測
pred_1 = model_1.predict(test_X)
# 実際の値と予測値をリストに追加
true_vals_1.extend(test_y)
pred_vals_1.extend(pred_1)
# 決定係数を計算し、リストに追加
r2_1 = r2_score(test_y, pred_1)
r2_scores_1.append(r2_1)
# 決定係数を表示
print("Average R^2 Score(LinearRegression / CV):", np.mean(r2_scores_1))
# YYプロットの確認
plt.figure(figsize=(5, 5))
plt.scatter(true_vals_1, pred_vals_1, color='blue')
plt.plot([min(true_vals_1), max(true_vals_1)], [min(true_vals_1), max(true_vals_1)], 'r--') # 対角線
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('YY Plot')
plt.grid(True)
plt.show()決定係数は0.92。マラソンタイムは現状の説明変数で十分説明できていそう。YYプロットは以下の通り。

さらに線形回帰以外のアルゴリズムでもモデルを作ってみよう。
まずはランダムフォレストから。いわゆる決定木と言われるものを複数作成し平均をとって最終的な予測値を決める手法。かなりメジャーなアルゴリズム。これで過学習を抑制できるらしい。
# ライブラリのインストール
from sklearn.ensemble import RandomForestRegressor
# モデルの構築
model2 = RandomForestRegressor(n_estimators=100, random_state=42)
# YYプロットと決定係数計算用のリスト作成
true_vals_2 = []
pred_vals_2 = []
r2_scores_2 = []
# クロスバリデーションを実施
for train_index, test_index in cv.split(X):
train_X, test_X = X.iloc[train_index], X.iloc[test_index]
train_y, test_y = y.iloc[train_index], y.iloc[test_index]
# モデルの学習
model2.fit(train_X, train_y)
# 予測
pred_2 = model2.predict(test_X)
# 実際の値と予測値をリストに追加
true_vals_2.extend(test_y)
pred_vals_2.extend(pred_2)
# 決定係数を計算し、リストに追加
r2_2 = r2_score(test_y, pred_2)
r2_scores_2.append(r2_2)
# 平均決定係数を表示
print("Mean R² Score (Random Forest / CV):", np.mean(r2_scores_2))
# YYプロットの表示
plt.figure(figsize=(5, 5))
plt.scatter(true_vals_2, pred_vals_2, color='blue')
plt.plot([min(true_vals_2), max(true_vals_2)], [min(true_vals_2), max(true_vals_2)], 'r--') # 対角線
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('YY Plot')
plt.grid(True)
plt.show()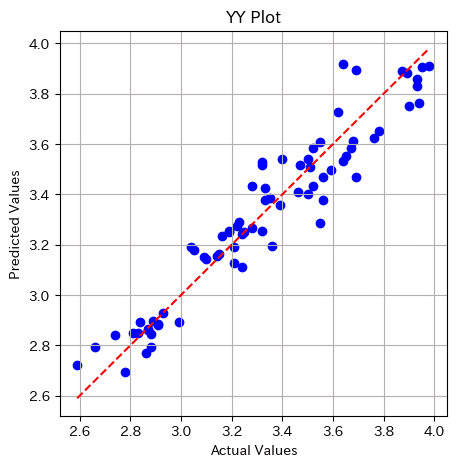
決定係数は0.91。線形回帰同様に予測精度は高い状況。
さらに、XGBoostでもモデルを作ってみる。
# ライブラリのインストール
import xgboost as xgb
# モデルの構築
model3 = xgb.XGBRegressor(objective ='reg:squarederror', n_estimators=100)
# YYプロット用のリスト
true_vals_3 = []
pred_vals_3 = []
r2_scores_3 = []
# クロスバリデーションを実施
for train_index, test_index in cv.split(X):
train_X, test_X = X.iloc[train_index], X.iloc[test_index]
train_y, test_y = y.iloc[train_index], y.iloc[test_index]
# モデルの学習
model3.fit(train_X, train_y)
# 予測
pred_3 = model3.predict(test_X)
# 実際の値と予測値をリストに追加
true_vals_3.extend(test_y)
pred_vals_3.extend(pred_3)
# 決定係数を計算し、リストに追加
r2_3 = r2_score(test_y, pred_3)
r2_scores_3.append(r2_3)
# 平均決定係数を表示
print("Mean R² Score (XGBoost / CV):", np.mean(r2_scores_3))
# YYプロットの表示
plt.figure(figsize=(5, 5))
plt.scatter(true_vals_3, pred_vals_3, color='blue')
plt.plot([min(true_vals_3), max(true_vals_3)], [min(true_vals_3), max(true_vals_3)], 'r--') # 対角線
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.title('YY Plot')
plt.grid(True)
plt.show()
決定係数は0.87。3種類のアルゴリズムを試したけど、いずれも高い精度で予測ができていることを確認。
最後に特徴量重要度とSHAPを確認したいと思う。
特徴量重要度、SHAPの確認
代表してランダムフォレストで作成したモデルを使用して、マラソンタイムへの各特徴量の影響を確認。
# 特徴量重要度の確認
## 特徴量重要度の取得
importances_2 = model2.feature_importances_
## 特徴量重要度を可視化
indices_2 = np.argsort(importances_2)[::-1]
features_2 = X.columns
## 特徴量重要度を降順にソート
sorted_importances_2 = [importances_2[i] for i in indices_2]
sorted_features_2 = [features_2[i] for i in indices_2]
## 特徴量重要度を可視化
plt.figure(figsize=(8, 5))
plt.bar(range(len(features_2)), sorted_importances_2, align='center')
plt.xticks(range(len(features_2)), sorted_features_2, rotation=45, ha='right')
plt.xlabel('Feature')
plt.ylabel('Importance')
plt.title('Feature Importance')
plt.tight_layout()
plt.show()
print()
#SHAPの確認
import shap
## SHAPのExplainerを初期化
explainer = shap.Explainer(model2, train_X)
## SHAP値を計算
shap_values = explainer.shap_values(test_X)
## 特徴量の重要度とSHAP値を可視化
shap.summary_plot(shap_values, test_X)結果は以下の通り
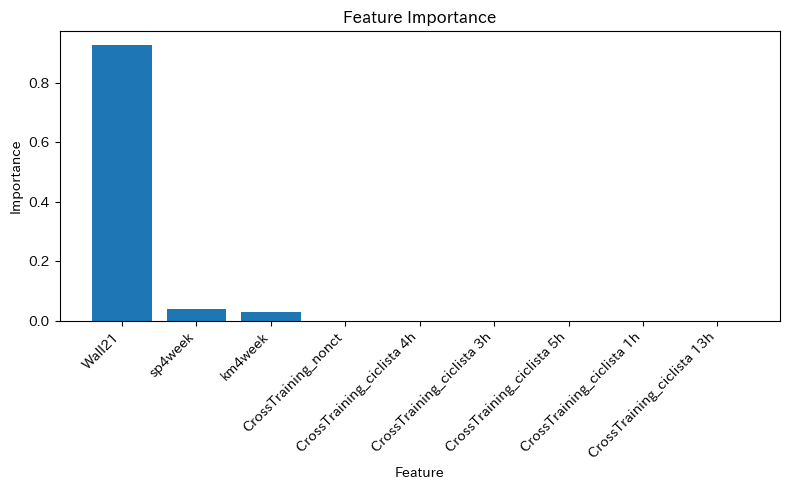

やはりWall21が特に効いてることを確認。また、Wall21の値が大きくなればなるほどマラソンタイムの値も大きくなるみたい。
Wall21が何を表している指標なのか、正直データの説明を見てもよくわからなかったのだけど、おそらく、前半タイムと後半タイムの比かと。だとしたら納得で、マラソンの世界だと「ネガティブラップ(前半より後半のペースを上げて走ること)」の方が良いタイムが出やすいとも言われていたりします。失速の影響って計り知れないんですよね…。私自身も何度も経験したなと。
最後に
半年前はデータ分析という言葉にすら抵抗を感じていた私ですが、なんとか形にはできたかなと思ってます。もちろん知識も経験も下の下の下なので、本当にスタートラインに立ったくらいのレベルですが、マラソンと同じでこのスタートラインに立てるかどうかがとても重要。そこに立てた自分にまずは拍手を送りたいと思います。
今後は実務の中でもAidemyで培った経験を活かし、さらに磨いていきます。
どんなことでも新しいスキルを身につけるって、とても気分が良いものです。新しい自分に出会えた的な感じ。
お読みいただいた方の中に、何か今の状況を変えたいと思っているけど動けずにいる方がいれば、やっぱり一歩踏み出した方が良いかなと思います。そんな方の背中をちょっとでも押せたら幸いです。
最後までお読みいただきありがとうございました。
