
bzip2を読む ハフマン符号2
こんにちは、junkawaです。
今回は、ハフマン符号化の符号長割当についてソースコードを交えて紹介します。
対象となる関数は BZ2_hbMakeCodeLengths() @ huffman.c です。
まず、符号を割り当てるための二分木(ハフマン木)を作ります。
bzip2の実装では、ハフマン木を配列のヒープ構造で表現します。
参考
https://ja.wikipedia.org/wiki/%E4%BA%8C%E5%88%86%E3%83%92%E3%83%BC%E3%83%97

上記図は、厳密には二分木ではないですが、一番上の根を無視して二番目のノードを根と考えると、二分木になります。
二分木にすることで、インデックス番号から簡単に親、子のインデックス番号を求めることができます。
例えば、インデックス番号 4 のノードの親ノードは、4を2で割った「2」となります。また、子ノードは、4に2を掛けた「8」と、それに1を加えた「9」となります。
このように、インデックス番号 i の親ノードのインデックス番号は i/2、子ノードのインデックス番号は i*2、i*2+1 となります。
符号長の求め方
必要な情報
入力:シンボルの出現頻度
出力:シンボルの符号長
処理の概略
1. 根が最小値となるような二分ヒープ木を構築(アップヒープ)
2. ヒープを使ってハフマン木を構築
a. 根から最小値を取り出し、木の最後のノード(配列の最後のノード)を根にセットして、木を再構築(ダウンヒープ)
b. 同上
c. 2、3 で取り出した2つのシンボル(一番小さい出現頻度と二番目に小さい出現頻度のシンボル)の出現頻度を合わせたノードを木に追加して、木を再構築(アップヒープ)。2つのシンボルを葉として、合わせノードを2つのシンボルの親とする
d. 2〜4を、全てのノードが合わさるまで繰り返す
3. 各葉(=シンボル)から根までの高さを符号長とする
bzip2-1.0.6では、符号長の最大値を17ビットとしています。割り当てた最大の符号長が17ビットより大きかった場合、符号長が短くなるように、出現頻度の重さを小さくして、1. 〜 6. を再実行します。
コードの紹介
BZ2_hbMakeCodeLengths() @ huffman.c
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/huffman.c#L63
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/huffman.c#L24
〜
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/huffman.c#L148
24: /*---------------------------------------------------*/
25: #define WEIGHTOF(zz0) ((zz0) & 0xffffff00)重み変数 weight から、シンボルの出現頻度を取得するマクロです。
26: #define DEPTHOF(zz1) ((zz1) & 0x000000ff)重み変数 weight から、ノードの結合(ADDWEIGHTS)回数を取得するマクロです。
27: #define MYMAX(zz2,zz3) ((zz2) > (zz3) ? (zz2) : (zz3))
28: zz2 と zz3 の大きい方を返すマクロです。
29: #define ADDWEIGHTS(zw1,zw2) \
30: (WEIGHTOF(zw1)+WEIGHTOF(zw2)) | \
31: (1 + MYMAX(DEPTHOF(zw1),DEPTHOF(zw2)))
32: 2つのノードを結合する時の重み計算用マクロです。
2つのノードの結合回数の多い方に、1を加算しています。これで、結合回数をカウントしています。
これにより、ノードの重みを比較する時に、結合した回数の多いノードがより重たくなり、ヒープ二分木の葉に近く配置されます。
例えば、UPHEAP で2つのノードの出現頻度(WEIGHTOF(zz))が同じ場合、結合回数(DEPTHOF(zz))の少ない方がヒープの根に近くなります。
こうすることで、結合した回数の多いノードが、(重みが最小となる)ヒープの根からノードが取り出されにくくなり、結合回数が多くなりすぎないようにしています。
結合回数が多くなると、parent から構成するハフマン木の高さが高くなります。したがって、これは、ハフマン木の高さを抑制するための措置です。
33: #define UPHEAP(z) \
34: { \
35: Int32 zz, tmp; \
36: zz = z; tmp = heap[zz]; \
37: while (weight[tmp] < weight[heap[zz >> 1]]) { \
38: heap[zz] = heap[zz >> 1]; \
39: zz >>= 1; \
40: } \
41: heap[zz] = tmp; \
42: }
43: heap 配列に要素を追加して、再構築するマクロです。
hepa配列のz番目の要素(heapの末尾)を、weight[z] が親より小さい場合、要素を親と交換して、heap構造の根に向かって上げていきます。
結果として、heap構造の根(heap[1])にweightが一番小さな要素が来ます。
コード中の zz >> 1 は、ヒープのインデックスzz の親ノードのインデックスを表します (zz/2 と同じ意味です)。
ヒープ heap の末尾にシンボルzを追加した後で実行されます。
(95行目のUNHEAPではシンボルz、109行目のUNHEAPではノードz)
44: #define DOWNHEAP(z) \
45: { \
46: Int32 zz, yy, tmp; \
47: zz = z; tmp = heap[zz]; \
48: while (True) { \
49: yy = zz << 1; \
50: if (yy > nHeap) break; \
51: if (yy < nHeap && \
52: weight[heap[yy+1]] < weight[heap[yy]]) \
53: yy++; \
54: if (weight[tmp] < weight[heap[yy]]) break; \
55: heap[zz] = heap[yy]; \
56: zz = yy; \
57: } \
58: heap[zz] = tmp; \
59: }
60:
61: ヒープ構造を一部だけ破壊して、再構築するマクロです。
ここのヒープ構造では、親ノードは子ノードより weight が小さい必要があります。したがって、破壊されたノード z (heap配列のz番目の要素) を起点として、子ノード(及び子孫のノード)と weight を比較し、親が子より weight が大きい場合に子とheapの値を交換します。
DOWNHEAPは、101、102行目から呼ばれますが、どちらもDOWNHEAP(1)として呼んでいるので、再構築した結果、weightが一番小さい要素がヒープの根(heap[1])に来ます。
yy が nHeap より大きい場合、調べきったということでループを抜けます(50行目)。この時、zzは葉ノードとなっています(yy=zz*2で、zzの子ノードyyが存在しないため)。58行目で、葉ノードzzにDOWNHEAP(z)のノードzの値を入れます。これは、ノードzの重さ weight が、子孫の中で一番大きかったということです。
yy が nHeap より小さい場合、左右の子でより小さい方(52,53行目でより小さい方をyyとしている)と、自身を比較し(54行目)、自身が小さければループを抜けて終了します。ループを抜けた先の58行目で、ループ中で入れ替えてきた最後の場所zzに自身をセットして、再構築を完了します。
自身が大きければ子供と自分を入れ替え、さらにその子供(zからみて孫)と比較を行い、自身の方が大きい場合、葉まで(子孫がなくなるまで)比較を続けます。葉までくると、yyがnHeapより大きくなるので50行目でループを抜けます。
yy が nHeap に一致する場合、子が一つしかないので、yyを比較対象の子として、yyがnHeapより小さい場合と同様の処理を行います。
52、53行目で、左右の子のより小さい方と親を交換する理由は、そうしないとヒープ構造が壊れることがあるからです。
左の子の重さが10で、右の子の重さが8、親の重さが11の場合を考えます。
左右の子で小さい方は右の方です。右の子と親を入れ替えると、親が重さ8、左の子の重さが10、右の子の重さが11で、ヒープ構造(親が子よりも重さが小さい)が保たれます。
ここで、左右の子で大きい方の左の子と親を入れ替えてみます。この場合、親が重さ10、左の子の重さが11、右の子の重さが8となり、親と右の子の重さがヒープ構造を満たしていません。
したがって、ヒープ構造を満たすために、左右の子のより小さ方と親を交換する必要があります。
62: /*---------------------------------------------------*/
63: void BZ2_hbMakeCodeLengths ( UChar *len,
64: Int32 *freq,
65: Int32 alphaSize,
66: Int32 maxLen )
67: {len:[出力] シンボルの符号長
freq:[入力] シンボルの出現頻度
alphaSize:[入力] シンボル数 (len配列、freq配列の有効なデータサイズ)
maxLen:[入力] 符号長の最大値
シンボルの出現頻度 freq から、シンボルの符号長 len を導出します。
68: /*--
69: Nodes and heap entries run from 1. Entry 0
70: for both the heap and nodes is a sentinel.
71: --*/heap、weight、parentはインデックス1から使用します。
これは、ヒープ構造の二分木を探索する時に、インデックス 1 から始まると都合が良いからです。
例えば、ノード番号 10 の親ノードはノード番号 5 ( 10/2 ) となり、ノード番号を2で割った値となります。逆にノード番号 10 の子ノードはノード番号 20、21 となり、ノード番号を2倍した値となります。
このように、ノードの親子間の移動が簡単に演算できるため、インデックスを 1 から始めます。
heap[0]、weight[0]、parent[0]は使用しません。センチネル(番兵)として、ループの終了確認などに利用されます。
UPHEAP時に、weight[0] が 0 なので、一番小さなノードは heap[0] として決定しているため、37行目のループは、heap[0]と比較した時に終了します。この時、実質的に一番小さなノードは heap[1] に入ります。
72: Int32 nNodes, nHeap, n1, n2, i, j, k;
73: Bool tooLong;
74:
75: Int32 heap [ BZ_MAX_ALPHA_SIZE + 2 ];ヒープ構造 heap は2つの用途に使用します。
1. ヒープソートにより、weightが最小のシンボルを見つける
91〜96行で準備して、101、102行でヒープから最小のシンボルを取り出します。
2. ハフマン木構築
100〜110行目で、ヒープから最小のシンボルを2つ取り出し、重さを足し合わせた新たなノードを1つヒープに追加します。この時、ヒープとは別のデータ構造 parent にハフマン木ノードの親子関係を保存します。ヒープはノードの重さによる親子関係の算出に利用します。
bzlib_private.h#115
115: #define BZ_MAX_ALPHA_SIZE 258BZ_MAX_ALPHA_SIZEは258です。MTF後のシンボルがEOB含めて最大で258個(0〜257 (s->nInUseが256の時)) となるためです。
番兵用の先頭を考慮して、配列サイズはBZ_MAX_ALPHA_SIZE+1必要ですが、DOWNHEAPで左右の子を見る場合に、2の倍数でないと配列の範囲外を参照する可能性があるので260となるBZ_MAX_ALPHA_SIZE+2で配列のサイズを取っていると思われます。
(厳密にはnHeapがしっかりしていれば起こりませんが)
76: Int32 weight [ BZ_MAX_ALPHA_SIZE * 2 ];シンボルの出現頻度をセットする配列です。
ハフマン木構築作業では、2 つのシンボルの重みをを結合したノードを作成します。その際にも使用します。
ハフマン木を構築する際、シンボル数分の葉ノードと、シンボル数-1の根・節点ノードが必要となります。これはと二分木の性質から求まります
シンボル数の最大値は BZ_MAX_ALPHA_SIZE なので、葉ノードと、根ノード、節点ノード全てを合わせると BZ_MAX_ALPHA_SIZE + (BZ_MAX_ALPHA_SIZE - 1) となります。
ここで、weight[0] をノードに用いない番兵として使用するので、これも加えて、BZ_MAX_ALPHA_SIZE + (BZ_MAX_ALPHA_SIZE - 1) + 1 で、合計 BZ_MAX_ALPHA_SIZE * 2 確保する必要があります。
77: Int32 parent [ BZ_MAX_ALPHA_SIZE * 2 ]; シンボルを2つ組み合わせたノードを作成し、それを親ノードとする時、親ノードの番号をparent[シンボル]に保存します。また、ノード同士を組み合わせるときにも使用します。
parent からハフマン木を構築することができます。
葉(シンボル)から、この親を辿って根まで到達するまでの数が、シンボルの符号長となります。
weight と同じく、parent もハフマン木のノード数分の要素が必要なため、BZ_MAX_ALPHA_SIZE * 2 確保する必要があります。
78:
79: for (i = 0; i < alphaSize; i++)
80: weight[i+1] = (freq[i] == 0 ? 1 : freq[i]) << 8;
81: シンボル i の出現頻度を1バイト左シフトして weight[i+1] にセットします。
シンボル 0 は、weight[1] に重みがセットされます。インデックスを 1 から始めるための処置です。
1バイト左シフトする理由は、weightの下位1バイトに、ノードが結合した回数を記録して重みボーナスとするためです。これについては105行目の解説で紹介します。
ここで、freq[i] が 0 の場合がありえるのか考えます。
s->inUseによって、MTF変換対象のシンボル’は連続値になり、全てシンボルは1回以上出現します。しかし、MTF変換ではシンボルの前回出現した間隔、に変換されます。freq は、その間隔が何度出現したか、を表します。前回出現した間隔(とランレングス符号化)は 0〜256 の値を取りうるのですが、必ず全ての間隔を取るわけではありません。したがって、ここで freq[i] が 0 となる場合はありえます。
80 行目の三項演算子で、freq[i] が 0 の場合、1 なので、出現頻度が 0 の場合と 1 の場合は同じ重みになります。
ちなみに、出現頻度が 0 なので、符号化されて出力されることはないので、長い符号を割り当てた方が得ですね。
82: while (True) {
83: 符号長が最大値maxLen(17ビット)以下になるまで、ハフマン木の構築を繰り返します。
84: nNodes = alphaSize;
85: nHeap = 0;
86: nNodes は、ハフマン木のノード数です。103 行目で親ノードを表す時に使用されます。
初期値として alphaSize、つまりシンボル数をセットします。
nHeap は、ヒープに追加したノードの数です。
87: heap[0] = 0;
88: weight[0] = 0;
89: parent[0] = -2;
90: ヒープ heap、重さ weight、親ノード parent のインデックス 0 を初期化します。
91: for (i = 1; i <= alphaSize; i++) {
92: parent[i] = -1;
93: nHeap++;
94: heap[nHeap] = i;
95: UPHEAP(nHeap);
96: }
97: 重さ weight が最も小さなノードが heap の先頭 (heap[1]) に来るように、heap にノードを一つずつ加えて再構築を繰り返します。ヒープソートの前処理と同じです。
ここで heap に入る値は、「シンボル+1」です。
heap[0] は番兵用に使用するため、シンボルの最小値が 0 であることに合わせて、「シンボル+1」としています。

右側がヒープ配列の中身、左側が木構造で表した図です。
図は、ヒープにシンボル0、1、2 を加えています。
ヒープのノードの値は「シンボル+1」なので、ノード内の数値としては、1、2、3 となっています。
シンボルの出現頻度は、1 > 0 > 2 の順とします。
weight[2] > weight[1] > weight[3] となります。
まず、UPHEAP(1)でシンボル0(ノード1)をノード0の子に追加します。ノード0は番兵です。ノード0のweightは最小なので、親子の入れ替えは発生しません。
次にUPHEAP(2)でシンボル1(ノード2)をノード1の子に追加します。シンボル1(ノード2)の出現頻度がシンボル0(ノード1)より高いので、親子の入れ替えは発生しません。
UPHEAP(3)でシンボル2(ノード3)をノード1の子に追加します。シンボル2(ノード3)の出現頻度がシンボル0(ノード1)より低いので、親子を入れ替えます。
98: AssertH( nHeap < (BZ_MAX_ALPHA_SIZE+2), 2001 );
99: nHeapが260(heap配列のサイズ)に収まっていることを確認します。
100: while (nHeap > 1) {101,102行で2個のノードをヒープから取り出しています。また、106〜109行で1個のノードを追加しています。
つまり、ループが1回回る毎にヒープから1つノードが減ります。
最終的にノードが1個(nHeapが1)になるまでループを回します。
この時、全てのシンボルのノードが結合され、ハフマン木が完成します。
ハフマン木はparentの親子関係に保存されています。ヒープはこのparentを作るために使用されます。
101: n1 = heap[1]; heap[1] = heap[nHeap]; nHeap--; DOWNHEAP(1);根ノード heap[1] は、現状で一番重み weight の小さな(出現頻度の低い)ノードです。これをn1に取り出します。
ヒープの末尾 heap[nHeap] を根ノード heap[0] にセットし、ヒープのサイズを減らし(nHeap--)、ヒープを再構築します(DOWNHEAP(1))。

図ではnHeapが9の時に、heap[1]の7をn1に取り出し、heap[nHeap]の1をheap[1]に入れています。
また、nHeapをデクリメントして8にして、二分木からheap[9]を削除しています。

上図は、DOWNHEAP(1)の実行を表しています。この時nHeapは8です。
前回の図で、heap[1]に1をセットしました。この時、heap構造が壊れてしまったので、DOWNHEAP(1)で再構築する必要があります。
ここで、シンボルの出現頻度を 0 > 8 > 5 > 1 > 3 とします。
最初に、47行目で tmp に heap[1] のシンボル0を入れます。
heap[1]を起点(zz=1)に再構築
DOWNHEAPの52行目でheap[1]の子であるheap[2]とheap[3]のweightを比較します(zzが1なのでyyが2)。
heap[2]はシンボル8、heap[3]はシンボル1なので、よりweightが小さいのはheap[3]のシンボル1です(heapに入る値は「シンボル+1」です)。
次に、54行目でheap[3]とheap[1](tmp)のweightを比較します。
heap[3]はシンボル1、heap[1]はシンボル0なので、よりweightが小さいのはheap[3]のシンボル1です。
したがって54行目でif文に入ってbreakしないで、55行目で、heap[1]にheap[3]を入れます(重みが小さいシンボルを根に近づけます)。
heap[3]を起点(zz=3)に再構築
52、53行目でheap[3]の子であるheap[6]、heap[7]のweightの小さい方を求めます。
heap[6]のシンボル1とheap[7]のシンボル5では、heap[6]のシンボル1の方が小さいです。
次に、54行目で(もともとheap[1]だった)tmpのシンボル0とheap[6]のシンボル1のweightを比較すると、heap[6]のシンボル1の方が小さいです。
したがって54行目でif文に入ってbreakしないで、55行目で、heap[3]にheap[6]を入れます(重みが小さいシンボルを根に近づけます)。
heap[6]を起点(zz=6)に再構築
49行目でyyは12となりますが、nHeapは8なので、50行目のif文でbreakしてループを抜けます。これは、葉ノード(heap[6])まで探索が終わったことを意味します。
58行目で、heap[6]にtmpのシンボル0を入れて、再構築を終了します。
再構築で起こった変化をまとめると、図の下段の配列の通りです。
heap[3]がheap[1]に入り、heap[6]がheap[3]に入り、heap[6]にもともとのheap[1]が入ります。
これは、もともとのheap[1]のシンボル0が一番weightが大きかったために、葉まで降りたきた、いうことです。
102: n2 = heap[1]; heap[1] = heap[nHeap]; nHeap--; DOWNHEAP(1);同上です。現状でweightが最小の根ノード heap[1] を n2 に取り出します。
103: nNodes++;
104: parent[n1] = parent[n2] = nNodes;親ノードの番号 nNodes (後述) をインクリメント更新します。
104行目で、新たなノードnNodesをn1,n2の親ノードとします。
これが重要で、parent にハフマン木の情報を保存しています。
105: weight[nNodes] = ADDWEIGHTS(weight[n1], weight[n2]);n1,n2の出現頻度を足して、親ノードnNodesの重みとします。
ここで、親の重みの下位1バイトに1を加え、ボーナスを与えます(31行目)。
足し合わされた回数の多いノードは、ボーナスが増えていきます。
足し合わされた回数のが多いノードは、ハフマン木の葉からの高さが高い、といえます。
こうすることで、出現頻度(weightの上位7バイト)が同じノードでも、子孫が少ない(下位1バイトが小さい)ノードの方がヒープの上に上がっていき、先に取り出され、結果としてハフマン木の高さが抑制され、符号長の最大値が小さくなります。
106: parent[nNodes] = -1;
107: nHeap++;
108: heap[nHeap] = nNodes;
109: UPHEAP(nHeap);新しく生成した親ノードをヒープに追加し、ヒープを再構築します。
ここで heap に入る値は、親ノードを識別する値です。
(91〜96行で heap に入る値は、「シンボル+1」でした)
シンボルは0〜alphaSize-1なので、シンボル+1は1〜alphaSizeです。
親ノードを識別する値は、alphaSize+1から始まる nNodes です。
nNodeは、シンボル+1 と重複しません。
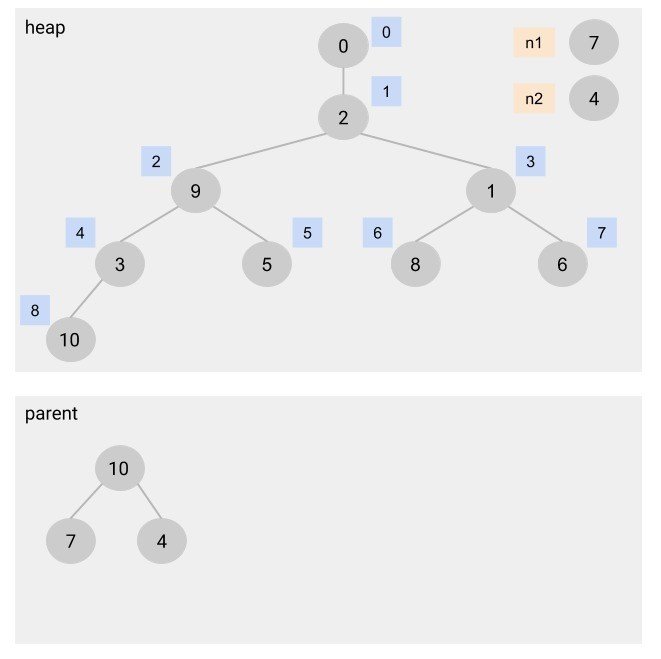
図は、シンボル7とシンボル4をn1とn2に取り出し、親ノード10を追加したものです。
上段はheapによる二分木で、ヒープソートにより出現頻度が最小のノードを取り出すために使用します。
下段はparent配列によるハフマン木で、heapから取り出した2ノードと、それらを結合した親ノードの関係を表します。
110: }
111: ヒープの要素数nHeapが1になるまでループを回します。
最後にヒープに残った要素 nNodes の親 parent[nNodes] のみが -1 で、それ以外の parent[i] (0<=i<=nNodes-1) は 0 以上の値が入っています。つまり、nNodes がハフマン木の根ということになります。
この時点で、符号長割当に必要な情報がparentに入っています。
これで、parentからハフマン木を構築できます。
112: AssertH( nNodes < (BZ_MAX_ALPHA_SIZE * 2), 2002 );
113: weight[nNodes]、parent[nNodes]が配列のサイズを超えていないかを確認しています。
114: tooLong = False;tooLongは、符号長が17ビットより大きい場合にTrueになります。
115: for (i = 1; i <= alphaSize; i++) {
116: j = 0;
117: k = i;
118: while (parent[k] >= 0) { k = parent[k]; j++; }
119: len[i-1] = j;
120: if (j > maxLen) tooLong = True;
121: }
122: parent から、符号長を取得します。
j が葉から根までの高さ、すなわち符号長です。
i が「シンボル+1」の値です。119行目で、i-1 として「シンボル」に戻してから、len[i-1] = j として、符号長をセットしています。
つまり、len[シンボル] = 符号長、となり、シンボルに符号長が対応付けられています。
118行目のwhileループですが、「シンボル+1」の葉ノード k から、parent を辿り、parent[k] が -1 になるまでループを回します。ループが一回回る毎に、jをインクリメントします。
100〜110行のヒープ再構築作業によって、全ての葉ノードは必ず親ノードを持ちます。したがって、118行目のループも必ず1回は実行されるので、符号長jは1以上になります。
123: if (! tooLong) break;
124: tooLongがFalseの時、すなわち符号長の最大値が17ビット以下の時、ループを抜け、終了します。
125: /* 17 Oct 04: keep-going condition for the following loop used
126: to be 'i < alphaSize', which missed the last element,
127: theoretically leading to the possibility of the compressor
128: looping. However, this count-scaling step is only needed if
129: one of the generated Huffman code words is longer than
130: maxLen, which up to and including version 1.0.2 was 20 bits,
131: which is extremely unlikely. In version 1.0.3 maxLen was
132: changed to 17 bits, which has minimal effect on compression
133: ratio, but does mean this scaling step is used from time to
134: time, enough to verify that it works.
135:
136: This means that bzip2-1.0.3 and later will only produce
137: Huffman codes with a maximum length of 17 bits. However, in
138: order to preserve backwards compatibility with bitstreams
139: produced by versions pre-1.0.3, the decompressor must still
140: handle lengths of up to 20. */
141: 1.0.3 から、最大ビット長を 20 から 17 に変えました。
圧縮率にほとんど影響しません。
伸長時には、下位互換性のため(古いバージョンで圧縮されたファイルへの対応のため) 20ビットまで考慮する必要があります。
142: for (i = 1; i <= alphaSize; i++) {
143: j = weight[i] >> 8;
144: j = 1 + (j / 2);
145: weight[i] = j << 8;
146: }重みを半分にしていきます、+1しているのは、jが小さくなった時に0にならないためだと思われます。
ビット長が長い場合に、この処理を繰り返していくと、出現頻度の差が無くなっていきます。
ヒープの再構築時に、ハフマン木の高さが低くなるように、結合されたノードの重みにボーナスを加えているので、出現頻度の差がなくなっていくと、ハフマン木の高さ、すなわち符号長は短くなります。
反面、出現頻度の低いシンボルに短い符号長を割り当てるという目的が一部達成できなくなるので(最適な割当でなくなるので)、圧縮率が下がります。
147: }最大符号長が17ビット以下の時、関数を終了します。
148: }まとめ
シンボルの出現頻度から符号長を割り当てる方法を紹介しました。
次回は、カノニカルハフマンによって符号長から一意に符号を割り当てる方法を紹介します。
ご覧下さりありがとうございます。いただいたサポートは図書館への交通費などに使わせていただきます。
