bzip2を読む ブロックソート7

こんにちは、junkawaです。

本記事では、前回に続きブロックソートアルゴリズムの「巡回行列のソート」についてソースコードを交えて紹介します。

今回の記事は、文に対して図が少なかったので追加してく予定です。

これまでの記事

https://note.mu/junkawashima/m/m3adbdc56f010

前回までのおさらい

ブロックソートでは、入力ブロックを巡回行列にして、各行をソートする必要があります。

bzip2では、このソートをStep1、Step2、Step3に分けて処理しています。

これまでの記事で、Step 1が完了するところまで紹介しました。

本記事ではStep 2について紹介します。

Step2

Step1では、先頭のシンボルがssで2バイト目がss以外のシンボルとなる行([ss,t]、t!=ss から始まる行)についてクイックソートしました。

Step2では、先頭がssで2バイト目がssとなる行([ss,ss]から始まる行)をソートします。

副産物で、Step2では、先頭がtで2バイト目がssとなる行([t,ss]から始まる行)もソートできます。

ソースコード紹介

mainSort()@blocksort.c
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/blocksort.c#L751

https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/blocksort.c#L911
〜
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/blocksort.c#L947

  911:       /*--
  912:          Step 2:
  913:          Now scan this big bucket [ss] so as to synthesise the
  914:          sorted order for small buckets [t, ss] for all t,
  915:          including, magically, the bucket [ss,ss] too.
  916:          This will avoid doing Real Work in subsequent Step 1's.
  917:       --*/

ここでは、大きなバケット[ss](ssから始まる行)をスキャンして、その行の先頭1文字前のシンボルt をソートします。これは、Step 1で未ソートの小さなバケット[ss,ss]([ss,ss]から始まる行)のソートも含みます。

Step 2で、[t,ss] から始まる行と[ss,ss] から始まる行のソートが完了するので、Step 1でこれらの行をクイックソートmainQSort3()する必要がなくなります。
そのために、946行目でSETMASKをつけることでソート完了を明示しています。

また、連続するssから始まる行(ssが4回連続する場合[ss,ss,ss,ss]など)のソートもここで完了します。

  918:       {
  919:          for (j = 0; j <= 255; j++) {
  920:             copyStart[j] =  ftab[(j << 8) + ss]     & CLEARMASK;
  921:             copyEnd  [j] = (ftab[(j << 8) + ss + 1] & CLEARMASK) - 1;
  922:          }

ここでは、copyStart、copyEndの値を初期化します。

図は ss が3の時の例です。

ftab[i] は、先頭2バイトがiとなる、ptr上での先頭インデックスです。

mainSort()の最初で実行される計数ソートによって、巡回行列の行は先頭2バイトでソート済みです。また Step 1 により、先頭2バイトが異なる行(例: [0,3])については、3バイト目以降もソート済みです。先頭2バイトが同じ行(例: [3,3])については、今回紹介するStep 2 でソートします。

図の例ではftab[3]は10で、これは先頭バイトが0で、2バイト目が3となる([0,3]から始まる) 行の行番号が ptr[10] から後に入っていることを表しています。
また、先頭バイトが1で2バイト目が3となる行は、1<<8 | 3 が259となるので、ptr[ ftab[259] ] から後に入っています。

copyStart[0]は[0,3]から始まる行番号を保持する、ptrの先頭インデックスで、図の例では10です。
同様に、copyStart[1]は[1,3]、copyStart[2]は[2,3]、...、となります。

copyEnd[0]は[0,3]から始まる行番号を保持する、ptrの末尾インデックスで、図の例では12です。これは、[0,4]から始まる行番号を保持するptrの先頭インデックス(ftab[4]、図では13)の一つ前の値です。

  923:          for (j = ftab[ss << 8] & CLEARMASK; j < copyStart[ss]; j++) {
  924:             k = ptr[j]-1; if (k < 0) k += nblock;
  925:             c1 = block[k];
  926:             if (!bigDone[c1])
  927:                ptr[ copyStart[c1]++ ] = k;
  928:          }

ここでは、[t,ss]から始まる行のソートを行います。ここでtは任意の0〜255のシンボルで、[ss,ss]から始まる行のソートを含みます。

もう少し細かく説明すると、ssより小さいuについて、[t,ss,u]から始まる行についてソートします。ssより大きいuの場合については、929行目以降でソートします。

ss=3の処理を図で説明します。

図中のftab[ss << 8] は、厳密にはftab[ss << 8] & CLEARMASKです。

この図では、923行目のfor文で jは400から419となります。
ftab[3<<8] はftab[768]でj=400。copyStart[3]は420なので、j<420より、jは419まで。
これは、prt上で、[3,0]から始まる行、[3,1]から始まる行、[3,2]から始まる行に対応します。
(後ほど説明しますが、ループの終了条件は変化していき、419が次第に大きくなっていきます)

924行目の k = ptr[j] - 1は、[3,0]から始まる行、[3,1]から始まる行、[3,2]から始まる行の、先頭から1バイト前のブロック番号となります。ptr[j]が0だった場合、kは-1となり、 if(k<0) k += nblock で、入力ブロックの末尾に巡回し、k=nblock-1となります。

c1 != ss の場合( [c1,3] から始まる行のソート)

ここでは、先頭ptr[j]から1バイト前のシンボルc1がssではない場合の説明をします。

図では、j=400の時、ptr[j]は1002なので、k = ptr[j]-1、つまり 1001 となります。また、c1 = block[1001]、つまり 1 となります。

1002から始まる行は、[3,0]から始まる行です。
blokc[1001]は1で、2バイト目のblock[1002]は3です。よって、1001から始まる行は、[1,3]から始まる行です。

ここからが面白い所なのですが、全ての巡回行列の行の中で、[1,3]から始まる最も小さい行は1001となります。
二文字目3から始まる行は、([3,3]から始まる行を除いて)Step 1でソート済みなので、3から始まる行の中で最も小さい値は、[3,0] から始まる行の ptr 上で一番最初にある、ptr[ ftab[3<<8 + 0] ]、すなわち ptr[400] で、1002 となります。
したがって、二文字目以降が一番小さい行の一つ前の文字c1(=1)から始まる行も、一番小さくなります。
よって、927行目で ptr [ copyStart[c1]++ ] = k として、copyStart[1]すなわち[1,3]から始まる行の先頭インデックス ptr[112]を 1001 で上書きしています。

ここで、元からあったptr[112]の値を退避しなくてよいのかと疑問に思いますが、ptr[ copyStart[i] ] から ptr[ copyEnd[i] ] の値は2文字目が3である行を指しており、また、3から始まるすべての行についてStep 2で処理をしていくので、その1文字前から始まるすべての行について、上書きをしていくので、元からあったptr[112]の値はその処理のどこかで出てくるため問題ありません。

次に、j=413の時を考えます。ptr[413] は2011なので k = 2010となります。また、c1 = block[201]、つまり 1 となります。
jが400から413までの間に c1 が 1 となる行がなかったと仮定します。
そうすると、[1,3]から始まる行で2番目に小さい行は 2010となります。
ここで、j=400の時の927行目で、 ptr[ copyStart[1]++ ] とcopyStart[1]がインクリメントされているため、j=413の時の927行目では、ptr[ copyStart[1]++ ] = 2010 は ptr[113] = 2010 となります。このように、ソート済みである、[3] から始まる行を小さい順にスキャンしていくと、その1文字前から始まる行(例 [1,3]) を自動的にソートできてしまいます。

ちなみに、926行目でif (!bigDone[c1]) と c1 から始まる行が全てソート済みか確認しています。ソート済みの場合、わざわざ ptr を更新する必要がないためです。

ここまでは、先頭ptr[j]の1文字前のシンボル c1 が 3以外となる行(ptr[j]-1が[c1,3]から始まる行)のソートについて紹介しました。

c1 = ss の場合 ( [3,3] から始まる行のソート)

ここでは、先頭ptr[j]の1文字前のシンボル c1 が 3 となる行(ptr[j]-1が[3,3]から始まる行)についてのソートについて紹介します。

図では jが403の時、ptr[j]は1501となり、kは1500となります。
1501行は3,1] から始まる行で、一文字前のシンボルc1が3なので、1文字前から始まる1500行は[3,3,1]から始まる行となります。

このとき、927行目で ptr[ copyStart[3]++ ] = 1500 となります。

この図では、3から始まる行を小さい順(j=400から順に)にスキャンしてきて、j=403で初めて1文字前c1が3となったとします。
ということは、この1500行は[3,3]から始まる行で一番小さいことになります。
[3,3]から始まる他の行と2バイト目以降を比較すると、一番小さくなるからです。
1500行における2バイト目以降とは、1501行のことです。

こうすることで、前述した ptr[ copyStart[1] ]に [1,3] から始まる行がソートされて入るのと同じように、ptr[ copyStart[3] ] に [3,3] から始まる行がソートされて入ります。つまり、[3,3]から始まる行も簡単にソートできます。

また、copyStart[3]++ となっているので、420→421とインクリメントされます。
これは次で説明する[3,3,3]から始まる行のソートに関係します。

ssが連続する場合 ([3,3,3,...] から始まる行のソート)

ここで問題となるは、3回以上連続するssから始まる行([3,3,3]から始まる行など)はどうやってソートされるのかどうか、です。

2回連続するssから始まる行(例 [3,3]から始まる行) は、前述したように [3,1] から始まる行がStep 1でソートされていることを利用して、[3,1]から始まる行の一つ前のシンボルが 3 である場合(つまり [3,3,1] から始まる、2回連続する3から始まる行)をソートできます。
これは [3,0]、[3,1]、[3,2]、そして後述する[3,4]、...、[3,255] から始まる行でも同様に行えます。

しかし、[3,3] から始まる行はStep 1でソートされていないので、[3,3]から始まる行の一つ前のシンボルが3である場合(つまり[3,3,3]から始まる、3回連続する3から始まる行)をソートできるのでしょうか。
結論から言うと、この場合もソートできます。

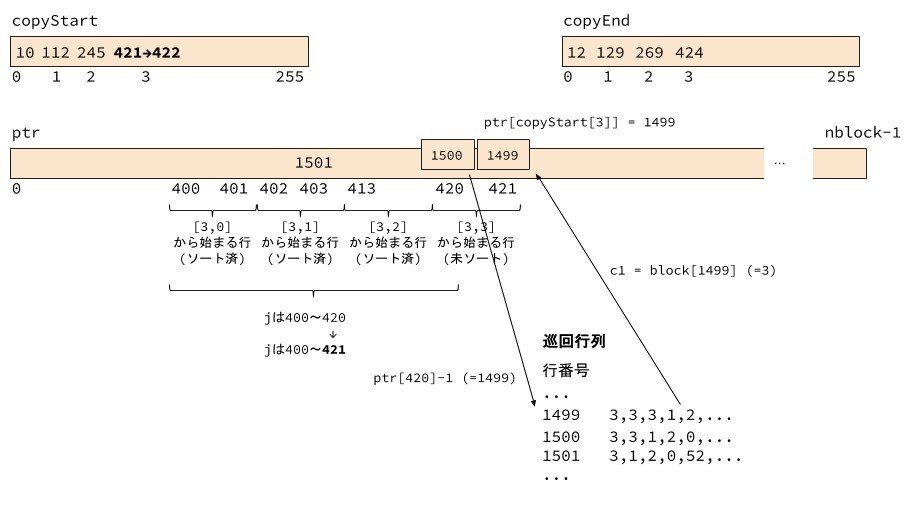
927行目の copyStart[c1]++ により、c1=3の時、copyStart[3]++となります。
copyStart[3] が 419 だった場合、インクリメントされて 420 になります。
923行目の forループの条件は j < copyStart[ss] で、ss=3なので、j < copyStart[3] となります。もともとは j < 419 だったのが、j < 420 となり、j = 420 の時も1文字前から始まる行のソートが可能になります。j=420は[3,3]から始まる行なので、これにより、[3,3]から始まる行の一つ前の文字から始まる行をソートすることができます。

図の例では、j=403の時に[3,1] から始まる行の1文字前が3なので、[3,3,1]から始まる行(1500行)のソート位置が決定され、ptr[ copyStart[3]] (=ptr[420])に 1500 が格納されます。

ループが回り、j=420となり、copyStart[3]で格納した1500行( [3,3,1] から始まる行)の1文字前のシンボル c1 が3の場合、それは[3,3,3,1] から始まる行となります。これも、他の行のソートと同様に、[3,3,1]から始まる行がソートされているので、その順序に従うと、その1文字前から始まる行もソートできます。

これは、[3,3,1]から始まる行の1文字前のシンボルが3以外の場合も、同様にソートされます。
例えば、[3,3,1]の1文字前が10だった場合、[10,3,3,1]から始まる行の先頭ブロック番号がcopyStart[10]にセットされます。

このように、ソート済みになった[3,3]のptrインデックスを利用して、[3,3,3]がソート済になります。次に、ソート済になった[3,3,3]のptrインデックスを利用して[3,3,3,3]がソート済になります。このようにして、連続する3から始まる行がソートされていきます。条件j<copyStart[3] のcopyStart[3]が増加することで、この処理が1つのループ内で行われます。自転車操業的なイメージですね。

一般化すると、Step 2でソートされるのは、[t,ssの連続] (tはssを含む0〜255)から始まる行となります。

  929:          for (j = (ftab[(ss+1) << 8] & CLERMASK) - 1; j > copyEnd[ss]; j--) {
  930:             k = ptr[j]-1; if (k < 0) k += nblock;
  931:             c1 = block[k];
  932:             if (!bigDone[c1]) 
  933:                ptr[ copyEnd[c1]-- ] = k;
  934:          }
  935:       }
  936: 

923〜928行では、前方([3,0]、[3,1]、[3,2]から始まる行の1文字前の行)からスキャンし、ソート結果を前方(copyStart)から保存していきました。

ここでは、後方([3,255]、[3,254]、...、[3,4]から始まる行の1文字前の行)からスキャンし、ソート結果を後方(copyEnd)から保存していきます。

ss=3の処理を図で説明します。

c1 != ss の時 ( [c1,3] から始まる行のソート)

929行目の for ループでは、j は 425〜629の降順で処理されます。

jの初期値 ftab[(ss+1)<<8] -1は、ss=3なので、ftab[1024] となり、630-1で629となります。これは、[4,0]から始まる行のptr上の先頭インデックスの一つ前のインデックス、すなわち [3,255]から始まる行のptr上の末尾インデックスとなります。これは[3]から始まる行の中で(辞書順ソートで)最も大きい行でもあります。

jは、629からデクリメントしていき copyEnd[ss] より大きい間、ループします。
ss=3なので、copyEnd[3]となり、これは図中では424となります。したがってjは425までとなります。copyEnd[3]は[3,3]から始まる行のptr上での末尾インデックスで、それより1大きいインデックスは [3,4]から始まる行のptr上での先頭インデックスとなります。

923〜928行で説明したのと同様に、[3,3]が連続する行がソートされると、このcopyEnd[3]がデクリメントされ、終了条件の425は次第に小さくなります。

図の例では、j=629の時、930行目で、k = ptr[j] -1 が k = ptr[629] -1 となり、ptr[629]が130なので、k = 129 となります。
ptr[629]が指す、巡回行列130行目(ブロック番号130)は[3,255]から始まる行で、[3]から始まる行の中で(辞書順ソートで)最も大きい行です。
この行の1文字前のc1はblock[129]より2となり、行(129)は[2,3]から始まる行となっています。
2文字目以降が[3]から始まる行の中で最も大きい行なので、129行は[2,3]から始まる行の中で最も大きい行となります。
したがって、copyEnd[2]、つまり[2,3]から始まる行のptr上でのインデックスの末尾ptr[269]に129をセットします。これは933行目の ptr[ copyEnd[c1]-- ] = k で行います。
copyEnd[2]-- とデクリメントしているので、このループにおいて次に[2,3]から始まる行が見つかった時は、その行は[2,3]から始まる行の中で2番目に大きい行となり、ptr[268]にセットされます。

c1 == ss の時 ( [3,3] から始まる行のソート)

図は j = 610 の時に、1文字前のc1が3となり、[3,3]から始まる行をソートする例です。

j = 610の時、930行目のk=ptr[j]-1が 1900-1となり、k=1899 となります。931行目のc1=block[k]はblock[1899]が3なので、c1=3となります。
1899行は[3,3]から始まる行です。この行の2バイト目以降は、すなわち1900行から始まる文字に一致します(厳密には最後の1バイトは除きます)。1900行は[3,254]から始まる行でptr上ですでにソート済みとなっています。ここで、j=611〜629の間に、1文字前が3から始まる行がなかったと仮定します。そうすると、1899は、[3,3]から始まる行の中で一番大きい行となります。この時、933行目でptr[ copyEnd[c1]-- ] = kとなるので、copyEnd[3] が424なので、ptr[424] に 1899 がセットされます。
こうして、[3,3]から始まる行のptr上での末尾(ptr[424])が、ソートされた結果(1899)で埋まりました。

ssが連続する場合 ([3,3,3,...] から始まる行のソート)

図は、[3,3,3]から始まる行をソートする例です。

一つ上の例(c1==ssの例)の続きとなっています。一つ上の例ではj=610の時にcopyEnd[3]--が起こり、copyEnd[3]は423になっています。
また、1つ上の例と今回の例の間に、[3,10]から始まる行で、その一つ前のシンボルが3だったとします。図中のptr[423] が3010 となっている部分です。このため、ptr[ copyEnd[3]-- ] = 3010 が起こり、copyEnd[3]は422になっています。

今回の例では、forループでjが下がっていき、j=424になった時の例です。
本来であれば424は[3,3]から始まる行の場所なので未ソートのため、jの範囲外ですが、j=610の時に、j=424の場所だけ[3,3]から始まる行の中でソート済みになったので、今回j=424でスキャン対象になります。
ptr[424]は1899で、その一つ前の1898行の先頭c1は図より3となります。したがって1898は[3,3]から始まる行となります。

ここで、1899行は[3,3]から始まる行の中で一番大きな行です。次に大きいのは3010行です。
1898行は、1899行より小さな行となります。これは、1899行が[3,3,254]から始まり、1898行が[3,3,3,254]から始まるからです。3バイト目を比較すると、1899行が254、1898が3となっています。
また、3010行は[3,3,10]から始まっており、1898行の[3,3,3]より大きいです。
929〜934行のループでは、[3,255]から[3,254]、[3,253]と[3]から始まる行を降順にスキャンして、ソート結果を後ろからセットしていくので、その1文字前が3となる、[3,3]から始まる行も大きい順に決まっていきます。
図の例では、[3,254]に対応するjをスキャンしている時に[3,3,254]が決まり、[3,10]に対応するjをスキャンしている時に[3,3,10]が決まり、[3,3]に対応するjをスキャンしている時に[3,3,3]が決まりました。
よって、1898はcopyEnd[3]が指しているptr[422]にセットされます。

入力ブロックが全て同じシンボルの場合

例としてシンボルが3の場合を考えます。

入力ブロックを生成する時のランレングス符号化により、全てのシンボルが3となることはありません。
全ての入力が3の場合、3,3,3,3,251,3,3,3,3,251,... と変換されます。

入力ブロック生成時のランレングス符号化について簡単に紹介します。

bzlib.c add_pair_to_block()#L216
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/bzlib.c#L216

L237〜L244
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/bzlib.c#L237

1が10回の場合、1,1,1,1,6
1が6回の場合、1,1,1,1,2
1が5回の場合、1,1,1,1,1
1が4回の場合、1,1,1,1,0
1が3回の場合、1,1,1
1が2回の場合、1,1
1が1回の場合、1

xが3回まではそのまま扱い、xがn回(n>=4)の場合、x,x,x,x,n-4、と4文字の後に残りの回数をセットします。

シンボルの連続が255回続くと、そこで一旦止めて、ランレングス符号化を行っています。
ADD_CHAR_TO_BLOCK() bzlib.c
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/bzlib.c#L260
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/bzlib.c#L276

前述のように、全ての入力が3の場合、3,3,3,3,251,3,3,3,3,251,... と変換されます。
これは、3を4回出した後で、残り回数である255-4の251を出力するからです。

では、全てのシンボル251の場合は、251,251,251,251の後に残り回数である255-4の251を出力するので、結局、全てのシンボルが251となります。

この場合、ftab[64256] (ftab[251<<8 | 251]) が 0 となり、ftab[64257]がnblockとなります。

ssが251の時、copyStart[251] = 0、copyEnd[251] = nblock-1となり、923行目のfor文と929行目のfor文はどちらも一回も実行されないです。

この場合について、下記のアサートにコメントがあります。

  937:       AssertH ( (copyStart[ss]-1 == copyEnd[ss])
  938:                 || 

[ss,ss] から始まる行が全てソートされた場合、copyStart[ss]-1 == copyEnd[ss]となります。ptr[ copyStart[ss]の初期値〜copyEnd[ss]の初期値 ] の範囲が過不足なく全てセットされたためです。

これがfalseの時、アサートします。

  939:                 /* Extremely rare case missing in bzip2-1.0.0 and 1.0.1.
  940:                    Necessity for this case is demonstrated by compressing 
  941:                    a sequence of approximately 48.5 million of character 
  942:                    251; 1.0.0/1.0.1 will then die here. */
  943:                 (copyStart[ss] == 0 && copyEnd[ss] == nblock-1),
  944:                 1007 )
  945: 

48.5 * 1,000,000 個の 251 は、入力ブロック生成時のランレングス符号化の結果、約 950,980 個の251になって入力ブロックに入ります。

シンボル251の255回の連続が251,251,251,251,251の5回に短縮(1/51)されるので、48.5 * 1,000,000 / 51 で、約 950,980 になります。

入力ブロックはデフォルトで900,000バイトなので、1入力ブロックが全て251でうまります(残りの50,980個は次の入力ブロックに入ります)。

この時、前述したように、923行目のfor文と929行目のfor文はどちらも一回も実行されないです。
したがって、copyStart[251] = 0、copyEnd[251] = nblock-1となります。

ちなみに、この入力において、ssが251でない場合、例えばss=0の時、ftab[0]、ftab[1]はどちらも0なので、Step1では、lo=0、hi=-1となり、892行目の hi > lo の条件がfalseとなり、897行目のクイックソートは実行されません。また、Step2では、ftab[0]とcopyStart[0]はどちらも0なので923行目のforループは実行されません。また、ftab[1]-1、copyEnd[0]はどちらも-1なので929行目のforループも実行されません。
ここで、copyStart[0]は0、copyEnd[0]は-1なので、937行目のアサート条件はtrueとなりアサートは発生しません。
ftab[0]〜ftab[64255]は全て0となり、ssが1〜250の場合、ss=0の時と同じ挙動となります。

ftab[64257]〜ftab[65535]は全てnblockとなります。この場合(ssが252〜255)も上記と同様に、Step1では、lo=nblock、hi=nblock-1となり、892行目の hi > lo の条件がfalseとなり、897行目のクイックソートは実行されません。また、Step2では、ftab[ss]とcopyStart[ss]はどちらもnblockなので923行目のforループは実行されません。また、ftab[ss+1]-1、copyEnd[ss]はどちらもnblock-1なので929行目のforループも実行されません。
ここで、copyStart[ss]はnblock、copyEnd[ss]はnblock-1なので、937行目のアサート条件はtrueとなりアサートは発生しません。

1.0.0と1.0.1では、943行目のアサート条件がありません。したがって、ss=251の時、copyStart[251] = 0、copyEnd[251] = nblock-1となってしまい937行目のアサート条件がfalseになり、アサートしてしまいます。
1.0.2以降では、943行目のアサート条件が追加されたので、アサートしません。

939〜942行のコメントは、このことについて記しています。

  946:       for (j = 0; j <= 255; j++) ftab[(j << 8) + ss] |= SETMASK;
  947: 

[t,3]から始まる行のソートが完了したので、ftabにSETMASKフラグをセットしています。

まとめ

先頭2バイトが同じ行のソートについて紹介しました。

Step2 では、[ss,ss]から始まる行だけでなく、もっと広範囲に[t,ss](0<=t<=255)から始まる行もソートできるのが驚きでしたね。

Step1とStep2を合わせて、[ss]から始まる全ての行がソート完了しました。

次に紹介するStep3では、[ss]から始まる行のソート結果を利用して、次回のStep1でのクイックソートの比較を高速化するための事前準備を行います。

お楽しみに。