bzip2を読む ブロックソート3

こんにちは、junkawaです。

本記事では、前回に続きブロックソートアルゴリズムの「巡回行列のソート」についてソースコードを交えて紹介します。

前回の記事

bzip2を読む はじめに
bzip2を読む ブロックソート1
bzip2を読む ブロックソート2

前回までのおさらい

ブロックソートアルゴリズムは
　1. 入力データを1字ずつずらして巡回行列を作る
　2. 巡回行列の行をソートする
　3. ソート後の行列の最後の列を出力とする

2. 巡回行列のソートでは、下記の1. 2. を行います。
　1. 先頭の2バイトでソート
　2. 先頭バイトのシンボルの出現頻度が少ない順に下記を行う
　　(3バイト目以降のソート)
　　a) 先頭2バイトが異なる値、の行をソート
　　b) 先頭2バイトが同じ値、の行をソート

本記事では、「先頭バイトのシンボルの出現頻度が少ない順」にソートする方法について紹介します。

先頭バイトのシンボルの出現頻度が少ない順にソートする

ソートには、シェルソートを使用します。ソート条件は、各行の先頭バイトのシンボルの出現頻度です。

ソート結果は配列runningOrderに保存し、後で使用します。

データ構造

入力：ftab[65535]

まず、前の記事で紹介した、先頭2バイトでのソート、によりftabがどのように変化したかを図示します。

ソート後のftab[i]は、積算後ftab[i] - 積算前ftab[i] となります。
(ソート処理時に、行の出現回数だけデクリメントされるため)

ソート後のftab[i]は、ptr中での、先頭2バイトがシンボルiから始まる行のブロック番号、の先頭インデックスとなります。

本処理でのソートは、先頭バイトのシンボルの出現頻度をもとに行います。
ftabは先頭2バイトのシンボルの出現頻度から生成されましたが、ftabと先頭バイトのシンボルの出現回数について説明します。

ソート後のprt には、先頭2バイトでソートされた、行の先頭ブロック番号が入っています。
先頭2バイトは「先頭バイト << 8 | 2バイト目」で表現しているので、先頭2バイトでソート済み = 先頭バイトでソート済み、となります。

例) 先頭2バイトが0〜255の時、先頭バイトは0。先頭2バイトが256〜511の時、先頭バイトは1。先頭2バイトが512〜767の時、先頭バイトは2。

先頭バイトのシンボルの出現頻度は、マクロBIGFREQを使用して取得します。

746: #define BIGFREQ(b) (ftab[((b)+1) << 8] - ftab[(b) << 8])

BIGFREQ(b)は、先頭バイトがシンボルbである行の数(頻度)を返します。

BIGFREQ(b) マクロ中の ftab[((b)+1) << 8] は、先頭バイトがb+1で2バイト目が0である行の、ptr 上での先頭インデックスです。また、ftab[(b) << 8]は、先頭バイトがbで2バイト目が0である行の、ptr 上での先頭インデックスです。

ptr にはソート済みの、各行の先頭ブロック番号が入っています。ftab[(b+1)<<8] - ftab[b<<8]は、先頭バイトがb+1となる行の先頭インデックスと先頭バイトがbとなる行の先頭インデックスの差分なので、先頭バイトがbとなる行の数になります。

出力：runningOrder[256]

   760:    Int32  runningOrder[256];

先頭バイトのシンボル(値)の出現頻度で昇順にソートした結果を、runningOrderに保存します。

処理の概要

シェルソートは、間隔の離れた要素の組でソートし、間隔をだんだん狭めていき、最終的には、隣接する要素同士の比較を行いソートします。隣接する要素同士の比較は、挿入ソートと同じ動作になります。

挿入ソートは、ほとんど整列されたデータに対して高速、という特徴があるので、間隔の離れた要素の組で予めソートすることで、挿入ソートを高速にすることが狙いです。

つまり、「予めソートするコスト < 挿入ソートの高速化するメリット」を期待しています。

下記は、間隔を121とした例です。

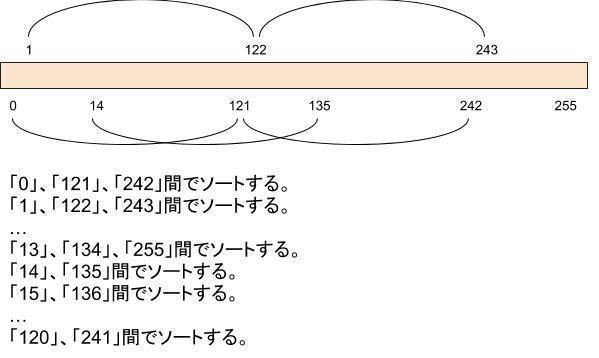
下記は、間隔を40とした例です。

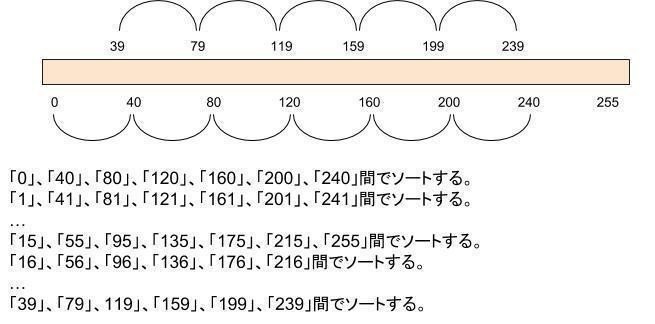
最終的に、間隔を1として全要素間でソートを行います。

次に、要素間のソートの方法を下記に記します。間隔を40とした例です。

円の大小は、先頭シンボルがrunningOrder[i]となる行の数、すなわちBIGFREQ(runningOrder[i])の大小を表します。

まず、1)でrunningOrder[0]の値の出現頻度(BIGFREQ(runningOrder[0]))と、runningOrder[40]の出現頻度(BIGFREQ(runningOrder[40])を比較し、出現頻度が小さくなる値をrunningOrder[0]にセットします。

次に、2)ではrunningOrder[40]の値の出現頻度とrunningOrder[80]の値の出現頻度を比較し、出現頻度が小さくなる値をrunningOrder[40]にセットします。

2-a)のように、runningOrder[80]の方の出現頻度がrunningOrder[40]の出現頻度より大きい場合、runningOrder配列に変化はありません。すでにrunningOrder[0]の出現頻度<runningOrder[40]が1)で成り立っているので、runningOrder[0]の出現頻度<runningOrder[80]の出現頻度が成り立つからです。

2-b)のように、runningOrder[80]の方の出現頻度がrunningOrder[40]の出現頻度より大きい場合、値を入れ替えた後、runningOrder[40]の値の出現頻度とrunningOrder[0]の値の出現頻度を比較する必要があります。runningOrder[40](元のrunningOrder[80])の出現頻度がrunningOrder[0]よりも小さい可能性があるからです。

ソースコード紹介

mainSort()@blocksort.c L832 〜 L861

   832:    /*--
   833:       Now ftab contains the first loc of every small bucket.
   834:       Calculate the running order, from smallest to largest
   835:       big bucket.
   836:    --*/

ここでいうsmall bucket(小さいバケツ)とは、(巡回行列の)各行を先頭2バイトで分類することです。big bucket(大きいバケツ)とは、各行を先頭1バイトで分類することです。

前回の記事で紹介したように、ftabは最終的に、ptrにソートされた、先頭2バイトシンボルの先頭インデックスを指しています。先頭2バイトが10の時、ptr で、先頭2バイトが10となるブロック番号を保存している場所は ptr[ ftab[10] ] となります。これが、"ftab contains the first loc of every small bucket."です。

   837:    for (i = 0; i <= 255; i++) {
   838:       bigDone     [i] = False;
   839:       runningOrder[i] = i;
   840:    }
   841: 

bigDoneは、本記事の対象外です。今回の記事で紹介する、先頭シンボルの出現頻度ソートの後で、3バイト目以降のソートを行う時に、先頭のシンボルがsとなる行全てのソートが完了したら、bigDone[s]=Trueとし、ソート完了の目印にします。

ここでは、runningOrderをインデックスiで初期化しています。

   842:    {
   843:       Int32 vv;
   844:       Int32 h = 1;
   845:       do h = 3 * h + 1; while (h <= 256);

hは、シェルソートの間隔を表します。ここでは、hは364と一意に決まるのですがあえて式を書いているのは、間隔にh = 3*h + 1 を使っていることを明示したかったからだと思われます。

上記式では、h=1→h=4→h=13→h=40→h=121→h=364 となり、hが決まります。

この h = 3*h + 1 で求まる間隔は、シェルソートでよく使われる間隔の一つです。間隔の詳細については、ShellsortのWikipedia を参照ください。

   846:       do {
   847:          h = h / 3;

間隔hを狭めていく処理です。

初回ループ時は、h=364→h=121となります。
ループが回る度に、hは下記のように変化します。
h=121→h=40→h=13→h=4→h=1

   848:          for (i = h; i <= 255; i++) {
   849:             vv = runningOrder[i];
   850:             j = i;

vv (runningOrder[i])を、今回のforループで新たに比較の組に加える値とします。

   851:             while ( BIGFREQ(runningOrder[j-h]) > BIGFREQ(vv) ) {
   852:                runningOrder[j] = runningOrder[j-h];
   853:                j = j - h;
   854:                if (j <= (h - 1)) goto zero;
   855:             }

BIGFREQ()でシンボルの出現頻度を比較します。

すでにソート済みの runningOrder[i-h]、runningOrder[i-h*2]、runningOrder[i-h*3]、...と、vv を比較し、vvより大きいものは順に右にずらして行きます。

   856:             zero:
   857:             runningOrder[j] = vv;

vvが収まる場所にセットします。このように、ソート済みの要素の間に、新たな要素vvを挿入するので、挿入ソートと呼ばれます。

   858:          }
   859:       } while (h != 1);
   860:    }

間隔h=1でソートされるまでループを回します。

下記に、具体的な比較内容を紹介します。

h=121の時

forループが i=121、vv=runningOrder[121]の時、whileループでは、BIGFREQ(runningOrder[0]) > BIGFREQ(vv)を比較する。

「先頭バイトが0となる行の数 > 先頭バイトが121となる行の数」のとき、runningOrder[121] = 0、runningOrder[0] = 121 とし、行の数の少ない先頭バイトの値(121)を、runningOrderの前([0])に配置する = 行数の少ない順にソートします。
ここでは、[0]、[121] 間で比較を行いました。

forループが i=122、vv=runningOrder[122]の時、whileループでは、BIGFREQ(runningOrder[1]) > BIGFREQ(vv)を比較します。
ここでは、 [1]、[122] 間で比較を行いました。
　　　　　　　　　　　　　　︙
forループが i=241、vv=runningOrder[241]の時、whileループでは、BIGFREQ(runningOrder[120]) > BIGFREQ(vv)を比較します。
ここでは、 [120]、[241] 間で比較を行いました。

forループが i=242、vv=runningOrder[242]の時、1回目のwhileループでは、BIGFREQ(runningOrder[121]) > BIGFREQ(vv)を比較します。
ここで、 [121]、[242] 間で比較を行い、[242]の出現頻度の方が小さかった場合、[121]と[242]で入れ替えを行い、2回目のwhileループで BIGFREQ(runningOrder[0]) > BIGFREQ(vv)を比較します。
ここでは、 [0]、[121]、[242] 間で比較を行いました。
　　　　　　　　　　　　　　︙
forループが i=255、vv=runningOrder[255]の時、、1回目のwhileループでは、BIGFREQ(runningOrder[134]) > BIGFREQ(vv)を比較します。
ここで、 [134]、[255] 間で比較を行い、[255]の出現頻度の方が小さかった場合、[134]と[255]で入れ替えを行い、2回目のwhileループで BIGFREQ(runningOrder[13]) > BIGFREQ(vv)を比較します。
ここでは、 [13]、[134]、[255] 間で比較を行いました。

まとめ

本記事では、「先頭バイトのシンボルの出現頻度が少ない順」にソートする方法について紹介しました。ソートにはシェルソートを用います。

先頭バイトのシンボルの出現回数をBIGFREQマクロから求めるところが面白かったのではないでしょうか。

次回以降は、こんかい求めた出現頻度が少ない順に、巡回行列をソートする方法を紹介します。