二項分布を理解しよう

先に大数の法則と中心極限定理の記事を出してしまいましたが、よくよく考えるとこっちが先でした。

なぜ正規分布ではなくて二項分布なのか理由を説明しますね。

二項分布は確率論の中でも歴史が深く他の正規分布やポアソン分布を生み出す基礎的な要素になっています。

まず二項分布に入る前に反復試行の確率を理解しておきます。

これは一回の試行で事象Aが起こる確率がpである独立な試行をn回行う。この時事象Aがちょうどr回起こる確率はq＝1ーpとする。これらを全て式で表してみると次のようになります。

例えばサイコロを5回投げて、そのうち3回、3の倍数がでる確率を求めるとします。ここでは事象Aを3の倍数とします。3の倍数が出る事象は{3, 6}ですね。すると一回サイコロを投げた時3の倍数が出る確率は1/3です。では次に事象Aの余事象（Aが起こらない確率）を求めます。3の倍数ではない事象は{1, 2, 4, 5}ですので、確率は2/3ですこれを先程の式に当て嵌めてみます。後はこれを計算すればちょうど3回出る確率を求めることができます。

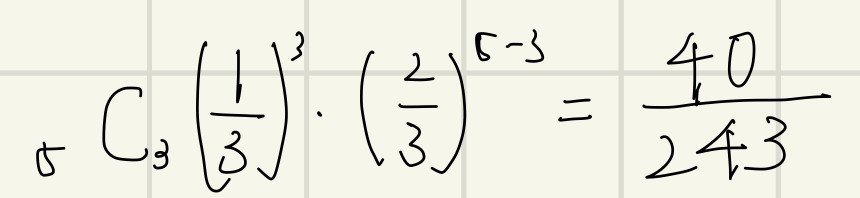
では二項分布に入っていきます。先程のrを確率変数のXと置きます。このXは確率分布表で表される確率変数になります。先程の反復試行の結果を確率分布で表したのを二項分布と言います。二項分布はbinomialのB（Bi）を使ってB(n, p)と表現することができます。

二項とh今回のサイコロの例なら3の倍数と3の倍数でないことを指します。ちなみにこの分布における確率の総和を二項定理によって求めるとちゃんと1になります。今回は省きます。

では早速二項分布の表を作成してみます。

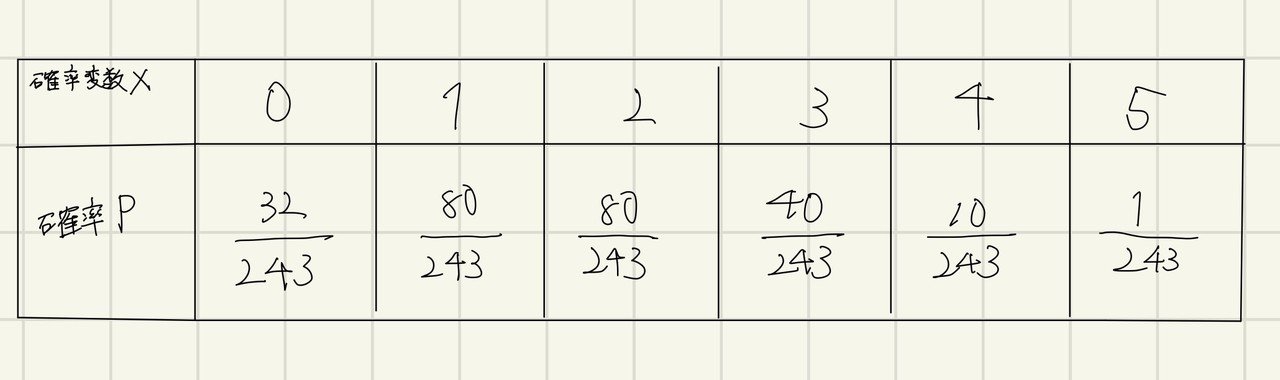
では次に二項分布の期待値E[X]と分散V[X]を求めます。

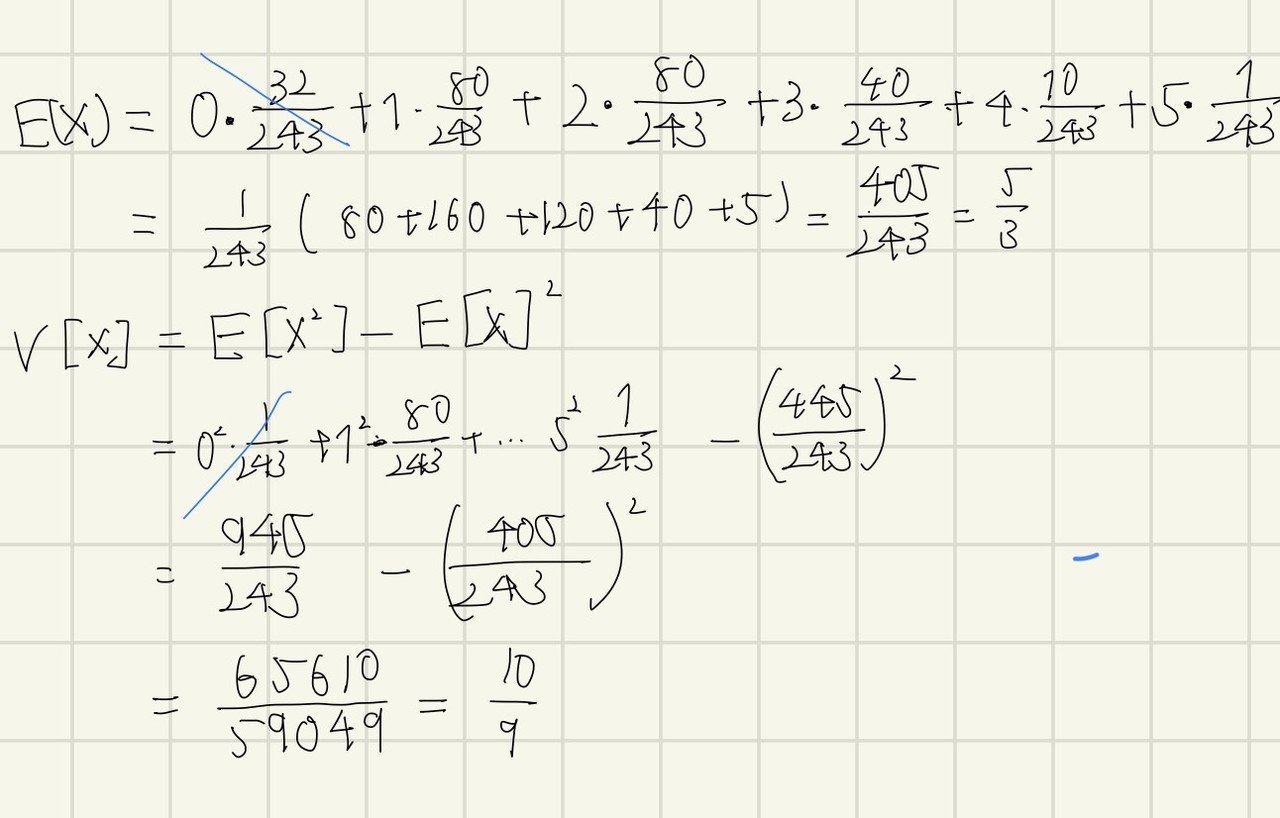
これを一般化すると次のようになります。nが試行回数でpが3の倍数が出る時の確率です。

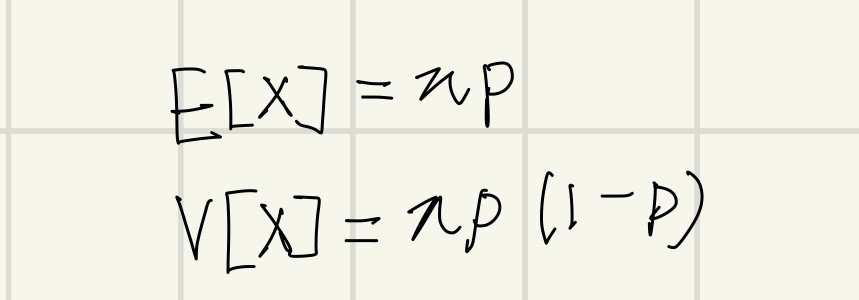
検算してみます。一致しました。

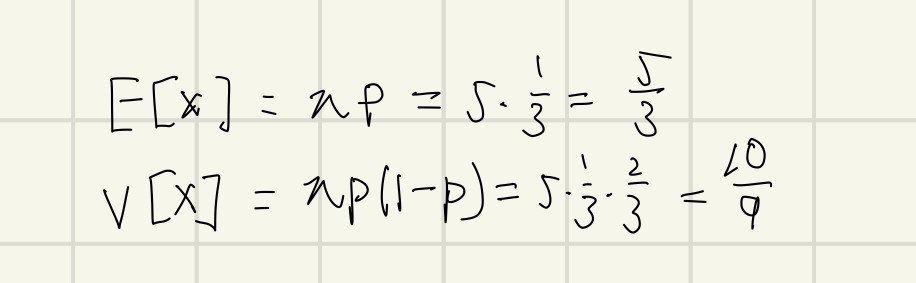
これで二項分布の基礎が終わりました。次は正規分布についてまとめます。