
最尤法を直感的に理解する
今回は最尤法について説明していきます。統計学や機械学習を触れていると一回位は聞いたことがあると思います。
最尤法ではあるデータから得られる確率を設定して、最良のパラメータを決定することが目的です。
と言ってもピンとこないと思うので具体例を交えて話してみます。例えばデータが10個あったとします。これを確率分布を用いてプロットしてみます。しかしどの確率分布を選べばいいでしょう。正規分布?指数分布?ガンマ分布?選択肢はあります。仮に正規分布を選んだとします。正規分布は平均と分散を求めれば分布を作ることができますが、最尤法の説明のため一旦除外します。
次のようにデータがあったとします。(汚いので見づらいかもしれません...すいません)

ではまず左側2.0の値を平均と置いて正規分布を置いてみます。見ても分かると思いますが、明らかに他のデータを説明できていませんね。

では次は右側の6.5?くらいの所を平均値だと設定します。先程よりは良くなりましたが、右側の方は説明できていません。
次に4.5?くらいの所を平均値だとします。そうするとかなりのデータが説明できていると思います。
何が言いたいのか。先程の分布から平均値が2.0になるのは直感的にもありえないですよね。確率的に言うと平均値が2.0になる確率は低いと判断できます。では平均値は6.5くらいの場合はどうでしょう。先程よりいい分布を見てしまっているため変だとは思いますが、一番最初の分布よりはいい感じに見えますよね。確率的に言うと平均値2.0の確率と平均値6.5の確率を比べた時平均値6.5の方が確率は高いと見ることができます。では最後に平均値4.5くらいの分布を見てみます。先程の二つの分布よりはいいように見えます。ちょっと汚いのですが、これを最適な分布だとします。他の平均値を採用した場合の直感的な確率を分布してみます。そうなると平均値4.5とした分布は他のどの平均値よりも確率が高いと見ることができます。(汚い&確率は適当です)
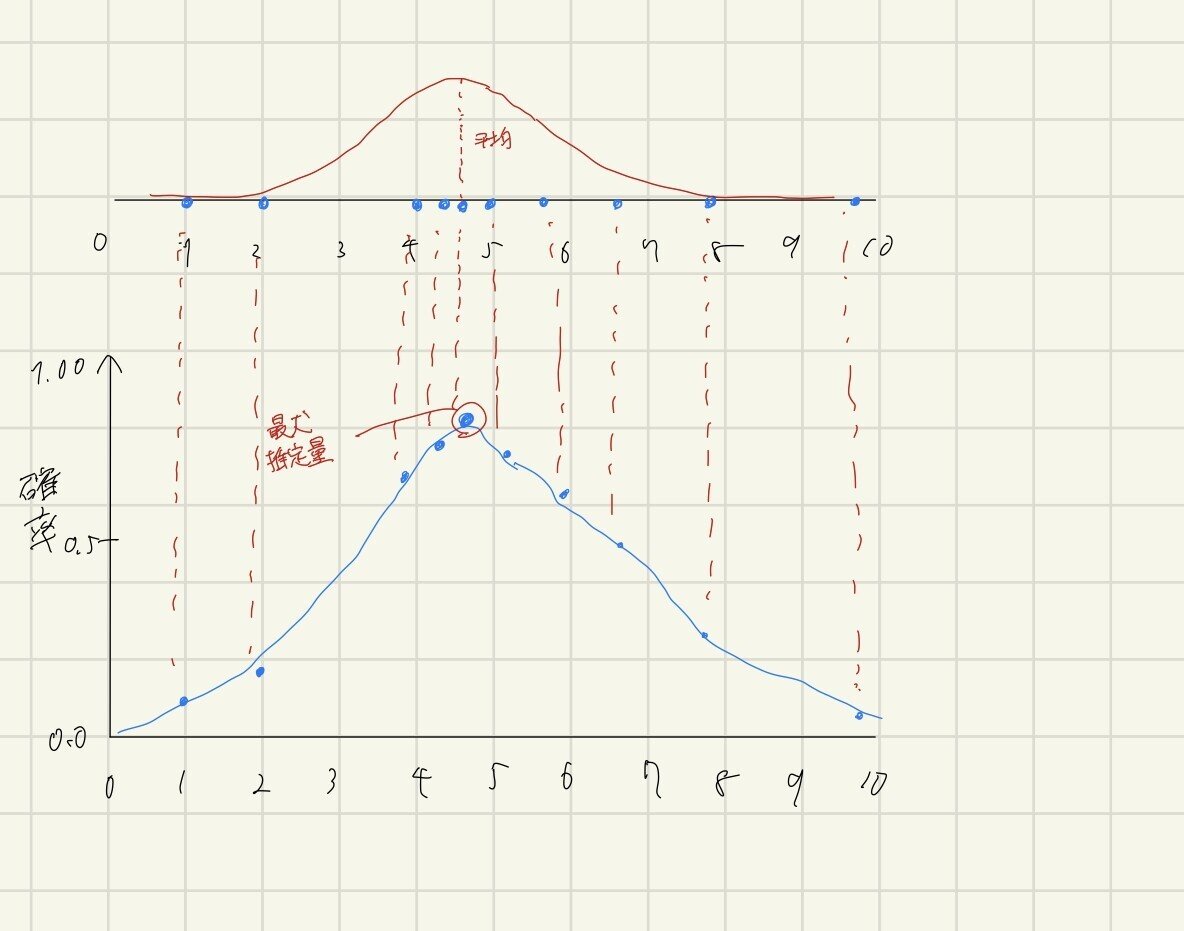
これを直感的に求めるのではなく確率を用いて最適なパラメータ(今回は平均値)を求めるのが最尤法です。また平均値が4.5の時確率が最も高くなったのでこの平均値を最尤推定値と言います。
実際には次の尤度関数を用いて最尤推定量を求めます。普通このまま扱うと計算しづらいので、対数変換します。そうすると尤度関数ないの積が加法によって求まるので、普通はこの対数変換した対数尤度関数を用います。サイコロやコインを使えばもっと簡単に計算できると思いますが、図式化したかったので正規分布を用いました。

・注意
ただあくまでこれが正解とは限りません。標本と母集団の関係を知っている方ならば理解できると思いますが、よく標本平均は母平均と一致すると扱われていいますが、これは中心極限定理を用いて近似的に母数の値を使っているので厳密には一致しません。
・参考
↑今回の記事作成にあたって非常に参考になった動画です。
