【物理/力学】§2 速度と加速度
1. 変位・速度・加速度
物理を始める上で,まずは速度などの定義をしましょう。力学において,切っても切り離せないのは変数である時間$${t}$$です。今回は,この時間に注目していくことになります。では,まず変位$${x(t)}$$について導入します。
変位
とある人が地点AからBまで移動するとき,そのベクトルを$${\overrightarrow{x_{1}}}$$とする。また,地点AからCまで移動するとき,そのベクトルを$${\overrightarrow{x_{2}}}$$とする。このとき,位置ベクトルの変化は$${\overrightarrow{x_{1}}-\overrightarrow{x_{2}}}$$と表すことができる。

よって,変位は$${\overrightarrow{x_{1}}-\overrightarrow{x_{2}}}$$と表せる。
2. 速度
「速さ」や「速度」などspeedに関する単語は複数あり,混合することが多いです。まずはこの2つの定義について確認しましょう。
「速さ」
速さとは,向きを持たない速さの数値を指す。数学的に言えば,速さはスカラー量なのです。つまり,北に30m/sで進んでも南東に30m/sで進んでも速さは30m/sとなります。
「速度」
速さと違い,速度は向きと数値を併せ持つ指標です。数学的に言えば,速度はベクトル量となります。これは,北に30m/s進むのと南東に30m/s進むのは方向が異なるので,速度は異なるということになります。
速さと速度を定義したところで,例題を解いてみましょう。
例題1. ある物体が時刻$${t_{1}}$$において位置$${x_{1}}$$にあり,時刻$${t_{2}}$$において位置$${x_{2}}$$にまで移動するとする。このとき,以下の問いに答えよ。なお,図は以下を参照せよ。

問 物体の平均の速度を求めよ。
解答
物体は,$${x_{1}}$$から$${x_{2}}$$まで進むとき時間は$${t_{2}-t_{1}}$$だけかかる。平均の速度は,この移動の平均の速度ということであるので,距離/時間という公式を適用すればよく(中学理科の知識/数学の知識),$${\overline{v}=\displaystyle\frac{x_{2}-x_{1}}{t_{2}-t_{1}}}$$が答えとなる。
この問題からわかる背景について考えましょう。今回は平均の速度を求めましたが,各点における速さも求めることが可能です。

以上の板書から分かるように,瞬間の速さを求めるには,$${t+\varDelta t}$$を$${t}$$に近づけるlim操作をします。上図では$${\varDelta t\to0}$$となっていますが,やりたいことは同じですね。結論として,瞬間の速さは変位の微分で求めることができるというわけです。
2. 加速度
加速度とは,単位時間あたりの速度の変化をさします。つまり,加速度が存在するとは,速度が刻々と変化しているということなのです。あの電車段々加速しているなー,とかいうのは加速度が発生しているということです。以下の板書を参照してください。
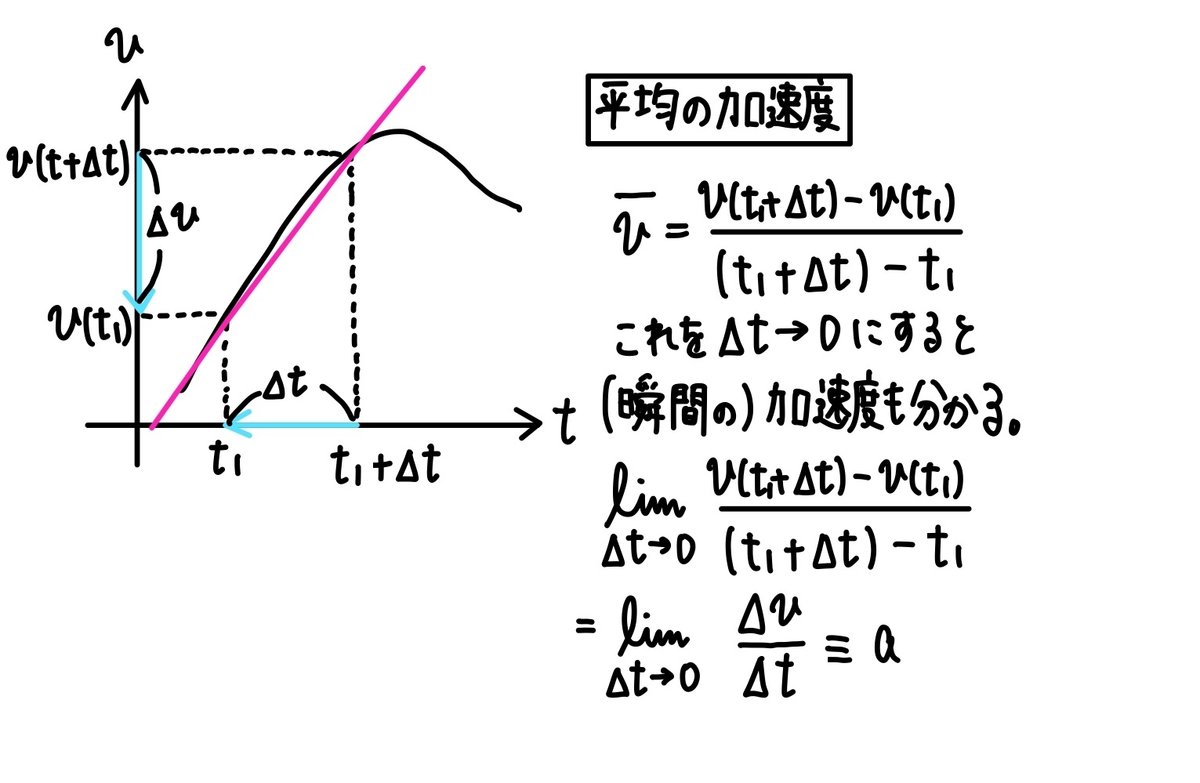
補足. 微分記号
一般に,$${x}$$を1階微分することを$${\dot{x}}$$,2階微分は$${\ddot{x}}$$と表します。すなわち,加速度については$${a=\ddot{x}}$$と表せるわけです。以降,数式の記述にこちらの微分記号を使用しますので,ご承知おきください。
いかがだったでしょうか。今回は加速度と速度について導入しました。次回は,具体的に速度と加速度を求める問題を扱います。次回,復習テストを実施しますので,復習しておきましょう。では,また次回!
(こちらのnoteを始めたのが10月であるため,今後物理の更新の順序が入り乱れる可能性が高いです。いきなり原子物理などを上げることもあるかと思いますが,ご承知おきください。)
