
確率の「独立な試行」はなぜ掛け算?
こんにちは。はじめまして。ワクワクと申すものです。
理系の大学生をやっていて、これが生まれて初めての投稿です。
学生をやっていると、勉強していて「これ、どうしてそうなるんだっけ?」といった、ちょっとした疑問が出てきます。
そしてそれが、腑に落ちるまで時間がかかる疑問だったりします。
それらと向き合っていると、時に、解決したときに感動を覚えることも。
ここでは、大学で統計学を学んでいて疑問に感じた、確率の問題で扱う「独立」という言葉の意味について、直感的に、理解できた(と思う)内容を書いていこうと思います。
一人の学生のアウトプットとして見てくださるとありがたいです。
背反と独立は別物!!
独立の試行の問題で最初につまづいたのは、背反と独立の区別でした。
(以下、全事象Uの部分集合である2つの事象をA、Bとします。)
背反事象とは、『ある試行において、一方が起これば他方は決して起こらないときの、それぞれの事象(デジタル大辞泉より)』であり、ベン図でいうと、AとBのマル同士が離れているイメージです。
例えば、ジョーカーを除くトランプを無造作に選んで、スペードを引く事象と、ダイヤを引く事象のように、同時に起こり得ないもの同士を背反であると言います。(下図)

次に独立事象について、独立と聞くと、「互いに関係がないもの」として、先ほどの背反事象と混同してしまいそうです。(これって私だけ?)
しかし、よく調べてみると、独立の問題には、「A∩B」が存在しているときに限っていました。逆に、背反事象の場合、A∩Bに中身がなく、実質存在していません。
(以下A∩Bを「積事象」と呼ぶことにします)
改めてデジタル大辞泉より、独立事象とは、『二つの事象において、一方の起こる確率と他方の起こる確率とが、互いに何ら影響を与えないような関係にあること』と言われています。ここについてはのち程見ていきます。
まとめると、背反が「全く関係なし!」なのに対し、独立は「関係は持っているけど、互いに刺激しない、程よい関係にある」ということが言えます。
「条件付き確率」から見た独立
さて、独立のイメージをつかんだ所で、数学的な見方で追っていきます。
確率の表記は、P(A)>0、P(B)>0のようにあらわすこととします。
P(U)=1として、A∩Bが存在するとき、A∩Bの確率はP(A∩B)>0となります。

上の図のように具体的な数字を使って確率を計算してみます。
P(A)=13/52=1/4 P(B)=4/52=1/13 P(A∩B)=1/52
ここで、事象Aが起こった上での事象Bの確率を考えてみます。これを条件付き確率といいます。この確率は、基準となる事象Aを後に書いてP(B|A)と表わすこととします。あくまでも、Bに該当する確率です。
Aを全体として見立てると、Bに該当するのはA∩Bの積事象だけです。
式で書くと、 P(B|A)=P(A∩B)/P(A)
となります。※ここまでが前振り
長くなってしまいましたが、ようやく「独立」について説明していけます。
独立であるというのは、「事象Aと事象Bの起こる確率が互いに影響しない」ということでした。これを式で表すと、
P(B)=P(B|A) あるいは、P(A)=P(A|B)
となります。(( ^ω^)・・・は?)
私には、これが理解できませんでした。図に書いて整理してみます。


上図によると、それぞれの確率は黄色枠と赤枠の比で表されています。
・P(B)とP(B|A)の相違点
→全体とするものが、UとAで違うところ
・P(B)とP(B|A)の共通点
→Bに該当する確率であるところ
ここで注目したいのが、基準となる事象の規模が、UからAで52枚から13枚へと小さくなったとしても、事象Bの場合の数が、Aによる制限で、4枚から1枚へと同じ比率で減っていることから、結果的に確率が等しくなっているという点です。
つまり、独立というのは、「Bについて、Aという制限下であろうとなかろうと確率が同じである」と言うことができるのです!
これはAの確率でもいえることです。Bという制限下であろうとなかろうとAに該当する事象に対応する確率は同じになります。(1/4になるはずです!)
今更ですが、図に載ってある事象Aと事象Bは独立ということが分かります。
「独立な試行」はなぜ掛け算なのか
いよいよクライマックスです。
最後の疑問「なぜ確率同士を掛けるのか?」ということに向き合おうと思います。
そもそも、独立な関係というのは、『背反と独立は別物!!』で述べたように、「互いを刺激しない、程よい関係」でした。
実際、そのような関係になる距離感をどうやって掴んでいるのでしょうか?
直感的な理解の前に、数式を用いて、独立のための条件を探ってみます。
条件付き確率の定義式 P(B|A)=P(A∩B)/P(A) ー➀
と、独立であるとき成り立つ関係式 P(B)=P(B|A) ー➁
を連立して、P(A∩B)について解きます。
➀を式変形して、 P(A∩B)=P(A)×P(B|A)
➁の条件より、 P(A∩B)=P(A)×P(B) ー③
と、簡単に求めることができました。
③式から、事象A、Bが独立であるならば、積事象の確率P(A∩B)は事象A、Bの確率の積と等しくなることが、数式から明らかになりました!
数学的に見ても、独立な試行での積事象の確率は、元の確率の掛け算と必ず等しくなる運命だったようです。
例題を使った考察
それでは具体的に、図と数字を使って、独立な関係とは、どのような距離感なのかを考えようと思います。
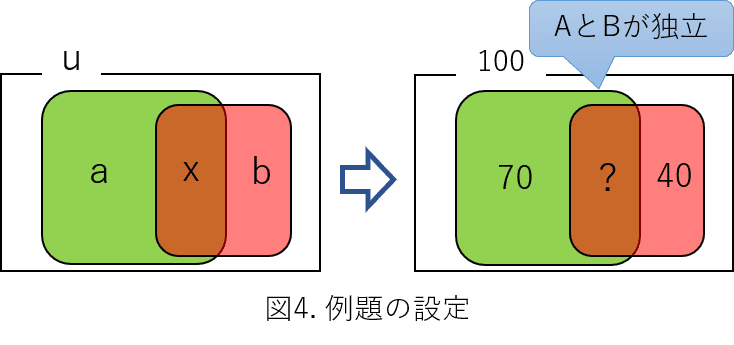
全事象Uの場合の数をu、事象A、Bの場合の数をそれぞれa、bとし、積事象A∩Bの場合の数をxとおきます。
AとBが独立であると仮定したときのxの値を求めることで、独立な試行と事象の距離感との関係を考察していきます。
まず、それぞれの確率を記号のままで出します。
P(A)=a/u P(B)=b/u P(A∩B)=x/u P(B|A)=(x/u) / (a/u)=x/a
ここで、上記の条件式➁に各々の確率を代入して、 b/u=x/a ー④
と表せます。④式をxについて解くと、 x=ab/u ー⑤
となり、AとBの独立が成り立つための、積事象の場合の数が求まりました。
さらに、⑤式を変形すると、両辺をuで割って、
x/u=ab/u² ∴x/u=(a/u)・(b/u)
となって、③式を導くことも出来ました。
次に数字を入れて実証してみます。
図4に従って、それぞれの確率を算出すると
P(A)=70/100 P(B)=40/100 P(A∩B)=x/100 P(B|A)=(x/100) / (70/100)=x/70
となります。
条件式➁に代入して、40/100=x/70 ∴x=28
と積事象の場合の数が具体的に求まりました。
そして、P(A∩B)=28/100 というのは、2つの確率P(A)とP(B)を掛けたものになっています! ( ∵(70/100)・(40/100)=28/100 )
最後に、P(A)とP(B)を固定したまま、xの値(2つの事象の重なり具合)を変えて比較評価してみます。

図5を見ると、(b)のように、お互いに離れすぎず、重なりすぎず、
P(A∩B)=P(A)×P(B)が成り立つような、丁度よい重なりのときに、独立の関係になれるということが分かります。
ちなみに、オレンジ枠で囲っている式を検証してみると、
P(B)=40/100=4/10 P(B|A)=28/70=4/10
となり、ちゃんと条件式が成り立っていることが確認できます。
まとめ
●積事象の有無によって、背反と独立を区別できる。
●独立の言葉の意味は、条件付き確率の観点から、「ある事象の確率が、他方の事象による制限の有無に関係なく変わらないこと」をいう。
●事象Aと事象Bが独立であるとき、AとBは、離れすぎず、また重なりすぎず、P(A∩B)=P(A)×P(B)が成り立つような、丁度よい距離感にある。
参考図書:高杉豊 馬場敬之 著、スバラシク実力が付くと評判の 演習 統計学
キャンパス・ゼミ 改訂2、p.007、マセマ出版社、(2017)
あとがき
最後まで読んでくださった方、お付き合いいただき有難うございました!
目的志向ではなく、自身が納得いくまでの過程を長々と書いたので、逆にわかりづらくなってしまったかもしれません。
しかし、根気強く裏付けを取りながら、問題と堅実に向き合うことに挑戦することができたと思います。良い経験になりました。
それでは失礼します。
