解説クラスTypeSf
解説クラスTypeSf
2024年2月22初講(初稿)
1.ヘッダーファイル
比較的、小サイズのヘッダーファイルなので全てNoteの
「code」機能で以下の様に示した後で解説して行きます!
// TypeSf.h: TypeSf クラスのインターフェイス
// TypeSf.h: TypeMB クラスのインターフェイス
//
//////////////////////////////////////////////////////////////////////
/********************************************************************************/
/***** 2値図形計測(フェレ・面積重心・慣性主軸等)情報用データ構造TypeSf *****/
/***** 重心や慣性主軸の算出をメンバ関数化したクラスに置き換えた *****/
/***** メモリ縮小版(フェレ・面積)情報用データ構造TypeMB{MeasureBase} *****/
/***** 2003年10月 6日:クラス化 *****/
/***** 2004年12月16日:メモリサイズ縮小版のTypeMB追加 *****/
/********************************************************************************/
#if !defined(AFX_TYPESF_H__D2B56FBF_E785_4922_B978_221A18C8927B__INCLUDED_)
#define AFX_TYPESF_H__D2B56FBF_E785_4922_B978_221A18C8927B__INCLUDED_
#include "ImageFuncDef.h" // 画像処理関数の定義部
#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000
class TypeSf
{
public:
TypeSf(); // コンストラクタ
virtual ~TypeSf(); // デストラクタ
public:
short x; // フェレ始点x座標
short y; // フェレ始点y座標
short h; // 水平フェレ径
short v; // 垂直フェレ径
short xl; // ラベル始点のx座標
short wh; // 水平幅
short whx; // 水平幅の始点x座標
short why; // 水平幅の始点y座標
short wv; // 垂直幅
short wvx; // 垂直幅の始点x座標
short wvy; // 垂直幅の始点y座標
int len; // 周囲長
int a; // 面積
float mh; // 1次水平モーメント
float mv; // 1次垂直モーメント
float mhh; // 2次水平重心回りモーメント
float mvv; // 2次垂直重心回りモーメント
float mhv; // 2次相乗重心回りモーメント
double al; // 慣性主軸角度
public:
double exe_cx(void); // 計測値加工:重心X座標算出
double exe_cy(void); // 計測値加工:重心Y座標算出
double exe_angle(void); // 計測値加工:慣性主軸角の算出
void exe_oval( // 計測値加工:等価楕円の算出
double& angle, // 角度の返値
double& r1, // 長径の返値
double& r2 ); // 短径の返値
};
struct TypeMB
{
short x; // フェレ始点x座標
short y; // フェレ始点y座標
short h; // 水平フェレ径
short v; // 垂直フェレ径
short xl; // ラベル始点のx座標
int len; // 周囲長
int a; // 面積
};
#endif // !defined(AFX_TYPESF_H__D2B56FBF_E785_4922_B978_221A18C8927B__INCLUDED_)(1)「#include」等、「#」構文を使用した先頭部分
#if !defined(AFX_TYPESF_H__D2B56FBF_E785_4922_B978_221A18C8927B__INCLUDED_)
#define AFX_TYPESF_H__D2B56FBF_E785_4922_B978_221A18C8927B__INCLUDED_
#include "ImageFuncDef.h" // 画像処理関数の定義部
#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000
「#if !defined(AFX_TYPESF_H__・・・」は、WindowsXP上
でVS(ヴィジュアルスタジオ、以下「()」内は省略し
VSと表記)が自動生成した、「#include」を多重に動作さ
せて無駄に定義をコンパイラシステムに読み込ませ無い工夫
としての「#if !defined()・・・#endif」構文です!
#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000
と3行もVSが自動生成したものでVSに取っての都合と
思って居るから、Windows以外のシステムをお使いの人は、
無くても良い物と思います!!
#include "ImageFuncDef.h" // 画像処理関数の定義部
この「#include」で「#define」定義した数値定数、及び、
この単純な型名の定義が記述された定義ファイルをインク
ルードする事を示します!
これらは、解説『エラーコード等各種単純定義』で説明して
居ます!
(2)クラス「TypeSf構文で定義」した!メンバー変数の定義概要
(2-1)項目図示
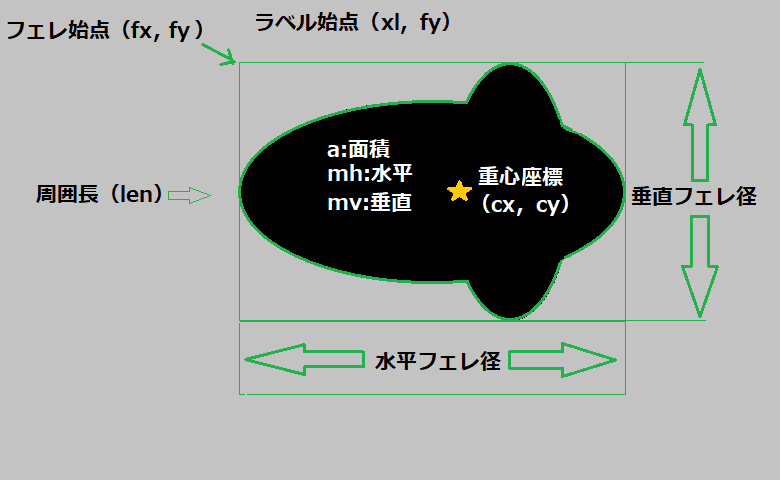
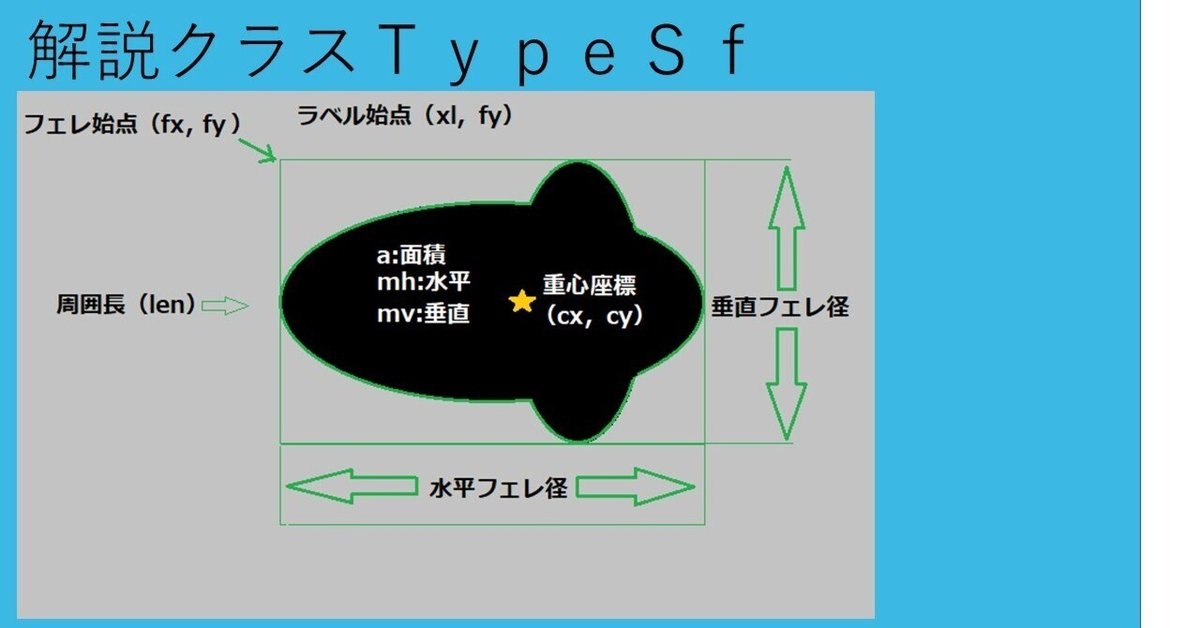
(2-2)座標
図(幾何図形計測項目)で示した座標として
フェレ始点(fx,fy)⇒メンバー変数(short x;shor y;)
ラベル始点(xl,fy)⇒メンバー変数(short xl;shor y;)
重心(cx,cy)⇒メンバー関数(double exe_cx();
double exe_cy();)で算出
ここでフェレ始点・フェレ径を説明します!図(幾何図形
計測項目)で示した様に緑色細線で矩形(長方形)で囲まれ
た図形の左上隅をフェレ始点とし図では(fx,fy)で示し、
ソノ図形の水平垂直の幅が
水平フェレ径=メンバー変数(short h;)と
垂直フェレ径=メンバー変数(short v;)に成ります!
フェレ始点・フェレ径が、「short型」なのは、画素単位と
して整数型で表現し実用的な最適(BYTE型では少ない、
int型では無駄に大き過ぎてメンバー変数格納メモリが大き
く成り過ぎる)なサイズと考えて、このサイズです!
★備考★図形上で示したフェレ径は、アクマデモ図形に矩形
を割り当てた定義上の物で図形の形によっては、一番長い
水平垂直幅とは異なる場合が有ります!
そして重心座標ですが、コレは、計測関数≪解説『
解説クラスFilter(○○)』で説明する計測関数「
int MeasureFere();int MeasureArea();
int MeasureMmt1();int MeasureMmt2();等」≫で計測し、
面積=メンバー変数(int a;)≪図では緑色の輪郭線で囲ま
れた黒色塗りつぶし図形の黒色画素を数えた物≫
水平1次モーメント=メンバー変数(float mh;)≪フェレ
始点を原点(fx,fy)とした黒色画素を以下で図示した
計算式「本当はTEX(テフ)が使えたら使うのだが、
筆者が理解出来て無いので図で示します」≫
同じく垂直1次モーメント=メンバー変数(float mv;)≪
フェレ始点を原点(fx,fy)とした黒色画素を以下で図示し
た計算式も図で示します≫
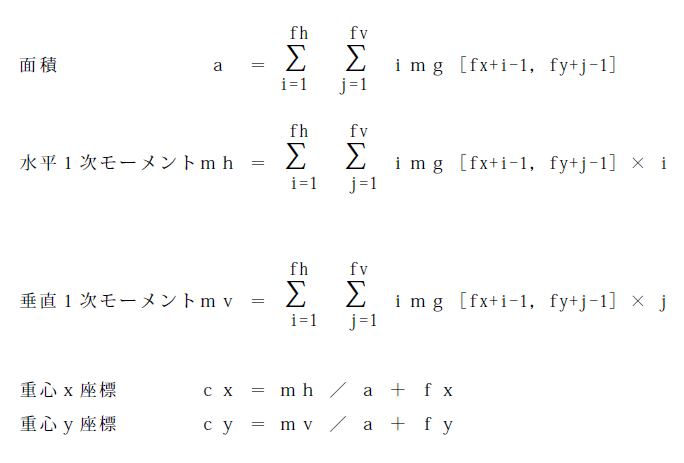
上記図の説明、先ず、「img[x,y]」は、画像を示し
画素は「0,1」の値で無い場合が「0」で有る場合が
「1」と数値的に存在する二次元配列だと考えて下さい!
「Σ」は、勿論、数学の式で合計(サメンション)を表す
アレです!ですから、その中で添え字(iおよびj)が
「Σ」の中で使用する変数で有ると理解して下さい!
更に説明は不要と思いますが、「=」は、左右の辺が同じ
値に成る事を示し、「×」は、乗算(掛け算)で「/」は、
左側の値を右側の値で除算(割り算)し、「+」は、加算(
足し算)です!そして数学の公式ですので依り内側の「Σ」
を先に演算し、後に外側「Σ」を計算します!
更に、面積の計算は、この二重「Σ」でフェレ径の中を舐め
て「1」の画素を合算するので幾何図形計測項目で示した
黒色の図形の面積に成る事は理解出来ますね!
そして水平1次モーメントは、内側の「Σ」で算出した値に
「×i」と外側の「Σ」での「i=1からfh」の添え字
「i」が乗算される事で面積の算出と違いX座標方向の位置
に依って重さが加わる事は理解出来ますね!
同じく垂直1次モーメントは、内側の「Σ」で算出した値に
「×j」と内側の「Σ」での「j=1からfv」の添え字
「j」が乗算される事で面積の算出と違いY座標方向の位置
に依って重さが加わる事は理解出来ますね!
メンバー変数(float mh;float mv;)と単精度浮動小数点型
で格納します!これで十分と判断し、出来るだけ高速処理を
追及した為にこの様にしました!
(2-3)長さ(サイズ)
(2-3-1)周囲長
周囲長(fx,fy)⇒メンバー変数(int len;)
と図(幾何図形計測項目)で示した様に緑色の輪郭線≪黒色
図形と空きとの間の線≫の画素数です!縦・横の数に関して
は、読者様の想像取りですが、斜めの場合、定義が有ります
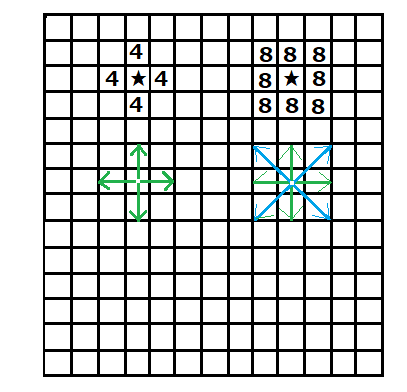
上図(連結)で示した様に緑色が画像処理用語「4連結」と
呼称する≪縦横が注視点(黒★)と結び付が有るとしてツナ
ガリが有ると言う意味≫連結間の長さは、画素単位で縦横共
1画素ですが、「8連結」と呼称する≪斜め方向(水色の線
)が注視点(黒★)と結び付が有るとしてツナガリが有ると
言う意味≫連結間の長さは、斜め方向の合計に
√2≒1.41421356を次のソースコード
「buf->len=len1+(int)((double)len2*1.41421356+0.5);」と
まず、「buf->len」はメンバー変数「int len;」への格納で
コード上の「len1」は、4連結成分の合計値で「len2」は、
8連結成分の合計値です!その「len2」に対して
「(int)((double)len2*1.41421356+0.5)」と「√2≒
1.41421356」★備考★無理数√2を中途半端な桁数で使用し
たのは、作成時の気分の問題で必要十分と考えたからです!
勿論、√2を係数として乗算したのは、斜めの長さだから増
えた割合を考慮したからです!そして「+0.5」で四捨五入を
「(int)で整数化≪整数型に変換する時は小数点以下は切り
捨てられる事はご存知ですね≫為に加えて四捨五入」し、
このクラスのメンバー変数「int len;」に格納し周囲長と
します!★備考★浮動小数型で無く整数型で格納したのは、
周囲長に関しては、元の濃淡画像の状態に2値化時に影響さ
れ小数点以下の値は、精度が悪いので無意味と思えるからで
す!
(2-3-2)フェレ径
図(幾何図形計測項目)で示した様に黒色図形を緑色細線矩
形が外形に接している事は、理解出来ますね!この水平フェ
レ径と垂直フェレ径と画像処理用語で呼称される
水平フェレ径=メンバー変数(short h;)と
垂直フェレ径=メンバー変数(short v;)に成ります!
何方も単位は、画素単位の整数型です!
(2-3-3)水平幅・垂直幅
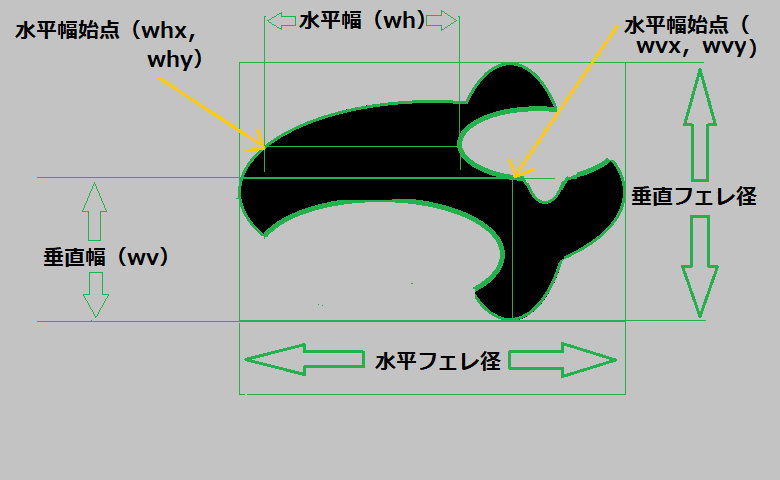
図(幅)に示した様に黒色図形の一番長い連続して水平・
垂直に一番長い幅が、
水平幅=メンバー変数(short wh;)と
垂直幅=メンバー変数(short wv;)に成ります!
そしてその始点
水平幅始点座標=メンバー変数(short whx;short why;)
垂直幅始点座標=メンバー変数(short wvx;short wvy;)
に成ります!
(2-4)面積・モーメント
「(2-2)座標」で重心の説明で図(重心等計算式)で
重心の算出する為に
面積=メンバー変数(int a;)
1次水平モーメント=メンバー変数(float mh;)
1次垂直モーメント=メンバー変数(float mv;)
をメンバー変数に格納する計測を行い、この面積と
1次モーメントから、重心をメンバー関数(メソッド)
≪double exe_cx(void);double exe_cy(void);≫を使用
して必要な所で重心座標を算出する事を紹介しましたが、
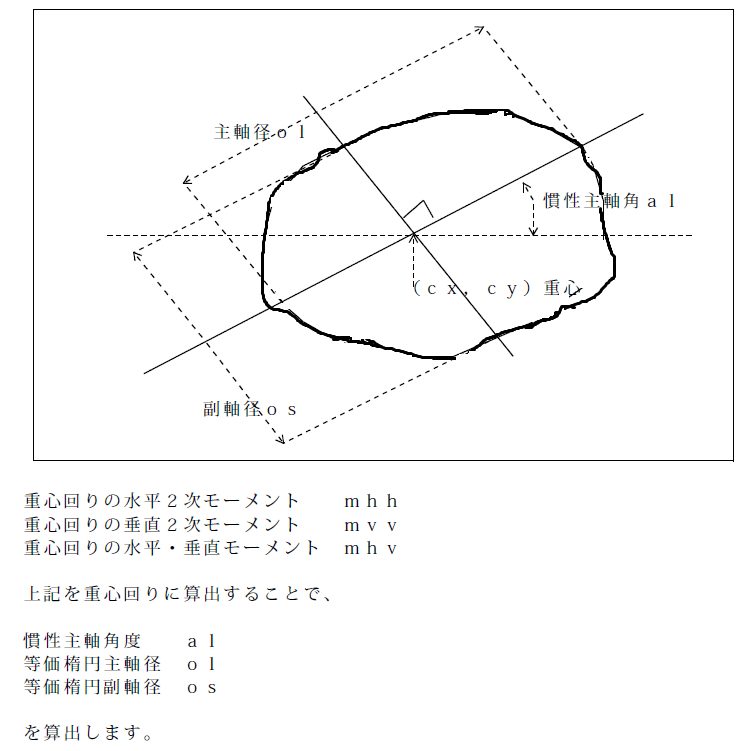
図(2次モーメント)に示した様に図形が楕円形と仮定した
場合の主軸(長い方の直径)・副軸(短い方の直径)の長さ
及び図で慣性主軸角と記載した傾きの角度を算出する
ソースコード「exe_angle(void)」は、
/************************************************************************/
/***** 計測値の加工:慣性主軸角の算出 *****/
/***** Tan(2 * t) / 2 = m11 / (m20 - m02) *****/
/***** という倍角で表現した関係式は *****/
/***** T**2 + [(m20 - m02) / m11] * T - 1 = 0 *****/
/***** ( T = TAN(t) ) *****/
/***** と書けるので、この2次方程式の解 *****/
/***** T = [M ± √(M**2 + 4)] / 2 *****/
/***** ( M = (m02 - m20) / m11 ) *****/
/***** ※注意※Y方向は-なので角度も-方向にする *****/
/************************************************************************/
double TypeSf::exe_angle(void)
{
double mhhD; // 水平モーメント値
double mvvD; // 垂直モーメント値
double mhvD; // 相乗モーメント値
double mm; // 途中の値
double da; // Δa
double db; // Δb
double alD; // 慣性主軸角
da = -1.0e-20; // Δaをセット
db = -da; // Δbをセット
mhhD = mhh; // 水平Moment取出し
mvvD = mvv; // 垂直Moment取出し
mhvD = mhv; // 相乗Moment取出し
if( mhvD > da && mhvD < db ){ // 相乗=微少 ならば
if( mhhD >= mvvD ){ // 水平≧垂直の時
alD = 0.0; // 角=0.0にし
}else{ // 水平<垂直の時
if( mhvD >= 0.0 ){ // 相乗が正なら
alD = PAI / 2.0; // 角=π/2.0にし
}else{ // 相乗が負なら
alD = -PAI / 2.0; // 角= -π/2.0に
} // する
} //
}else{ // ≠0.0 なら
mm = ( mvvD - mhhD ) / mhvD; // 左記を計算し
if( mhvD < 0.0 ){ // 相乗Momentが負
alD = atan( ( mm - // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
}else{ // 相乗Momentが正
alD = atan( ( mm + // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
} //
} //
alD = -alD; // 角度の符号反転※注※
al = (float)alD; // 一旦保存
return( alD ); // 慣性主軸角を返す
}と成り、コメントで判る様に「2次水平」・「2次垂直」
及び「2次相乗」と「mhh」・「mvv」・「mhv」と
メンバー変数
2次水平モーメント=メンバー変数(float mhh;)
2次垂直モーメント=メンバー変数(float mvv;)
2次相乗モーメント=メンバー変数(float mhv;)
を使用して算出します!
このメンバー変数「mhh」・「mvv」・「mhv」は、因みに、このメンバー変数は、ファイル「Filter240.cpp」に
if条件「if( d )」と有効画素がある場合は合計して
算出する事は理解して頂けますね?!暫くしたら、
解説『クラス解説クラスFilter(○○)』で説明
する予定です!参考までに
/************************************************************************/
/***** 2次モーメント計測:実行部:x方向 *****/
/***** 2次モーメントとのみ計測します *****/
/************************************************************************/
void Filter::lbl_mmt2_only_x(
short *px, // 画像始点:x方向
TypeSf buf[], // 計測結果Buffer
double y, // y座標 1.0~
int h // 水平幅
){
TypeSf *ptr; // 1次Moment結果Ptr
double x; // x座標 1.0~
double yy; // y座標の自乗
short d; // 画像データ
yy = y * y; // y座標の自乗算出
for( x = 1.0; --h >= 0; x += 1.0 ){ // x座標方向に繰返
d = *px++; // ラベル取出し
if( d ){ // 有効ラベル有り
ptr = &buf[ d ]; // 計測Ptr算出
ptr->mhh += (float)( x * x ); // 2次水平MMT計測
ptr->mvv += (float)yy; // 2次垂直MMT計測
ptr->mhv += (float)( x * y ); // 2次相乗MMT計測
} //
} //
}
/************************************************************************/
/***** 2次モーメント計測:実行部 *****/
/***** 2次モーメントとのみ計測します *****/
/************************************************************************/
int Filter::LabelingExecuteMoment2Only(
TypeArray *ps, // ラベル画像情報
TypeSf buf[] // 計測結果Buffer
){
short *p; // 画像Ptr
int h; // 水平幅
int v; // 垂直幅
double y; // y座標 1.0~
int inc; // 増加幅
if( ps == 0 ){ // 空情報なら
return( STI_ARY_0 ); // 左記を返す
}else if( ps->adr == 0 ){ // 空画像なら
return( STI_ARY_1 ); // 左記を返す
}else if( ps->w != 2 ){ // 非ラベル画像なら
return( STI_ARY_5 ); // 左記を返す
} //
p = (short*)ps->adr; // 画像Ptrを取出す
h = ps->h; // 画像のサイズを
v = ps->v; // 取り出し
inc = ps->inc; // 画像増加幅取出
for( y = 1.0; --v >= 0; y += 1.0, p += inc ){ // y座標方向に繰返
lbl_mmt2_only_x( p, buf, y, h ); // x座標方向に処理
} //
return( END_STI ); // 正常終了
}で、そのファイル「Filter240.cpp」の一部ソースコードを
示しました?!中身の解説は、
解説『クラス解説クラスFilter(○○)』に記載し
ます!
そして、ここのメンバー関数(メソッド)≪
double exe_angle(void); // 計測値加工:慣性主軸角の算出
void exe_oval( // 計測値加工:等価楕円の算出
double& angle, // 角度の返値
double& r1, // 長径の返値
double& r2 ); // 短径の返値
で「慣性主軸角」・「長径(長い方の直径)」・
「短径(短い方の直径)」を算出します!
★備考★メンバー変数「double al; // 慣性主軸角度」
に関しては、ここのメンバー関数で算出した値がセットされ
るで無く、解説『クラス解説クラスFilter(○○)』
で説明する予定です!
(3)クラス「TypeSf構文で定義」した!メソッド(メンバー関数)の定義概要
(3-1)コンストラクタ/デストラクタ
class TypeSf
{
public:
TypeSf(); // コンストラクタ
virtual ~TypeSf(); // デストラクタ
#include "TypeSf.h"実体は、ファイル「TypeSf.cpp」に存在!
//////////////////////////////////////////////////////////////////////
// 構築/消滅
//////////////////////////////////////////////////////////////////////
TypeSf::TypeSf()
{
}
TypeSf::~TypeSf()
{
}ここでは有るだけ、単に意味の有る実行は行いません!
(3-2)重心の算出
(3-2-1)関数「double exe_cx(void){・・・}」
double TypeSf::exe_cx(void) // 重心X座標算出
{
if( a != 0 ){ // 面積が有効ならば
return( (double)mh / (double)a + (double)x - 1.0 ); // 左記で算出
}else{ // 面積が0なら
return( 0.0 ); // 0にする
} //
}☆備考☆この関数はファイル「TypeSf.cpp」に存在!
★注意★この関数は「public:」属性ですのでライブラリの
外から使用可能です!
(3-2-1-A)関数「exe_cx()」の【関数名】
「exe」は、英単語「execution」の省略形で「実行」を意味
「cx」は、「c」が英単語「center」で「中央」ですが、
ここでは、重心とし「x」で重心X座標とします!それで
重心の計算を実行する関数です!
(3-2-1-B)関数「double exe_cx()」の【返値】
double TypeSf::exe_cx(void) // 重心X座標算出
{倍精度浮動小数点数型で算出した重心座標を辺値とし返しま
す!
(3-2-1-C)関数「exe_cx()」の【仮引数】
存在しません!
(3-2-1-D)関数「exe_cx()」の【アルゴリズム】
{
if( a != 0 ){ // 面積が有効ならば
return( (double)mh / (double)a + (double)x - 1.0 ); // 左記で算出
}else{ // 面積が0なら
return( 0.0 ); // 0にする
} //
}if分岐条件「if(a!=0)」と面積≪クラスのメンバー変数
「int a;」≫が有効(≠0)ならば、分岐中身
「return((double)mh/(double)a+(double)x-1.0);」と
1次水平モーメント≪メンバー変数「float mh;」≫を式
「(double)mh/(double)a+(double)x-1.0」で面積で除算する
事で算出し「+(double)x-1.0」とフェレ始点からの相対座標
に補正!
(3-2-2)関数「double exe_cy(void){・・・}」
double TypeSf::exe_cy(void) // 重心Y座標算出
{
if( a != 0 ){ // 面積が有効ならば
return( (double)mv / (double)a + (double)y - 1.0 ); // 左記で算出
}else{ // 面積が0なら
return( 0.0 ); // 0にする
} //
}☆備考☆この関数はファイル「TypeSf.cpp」に存在!
★注意★この関数は「public:」属性ですのでライブラリの
外から使用可能です!
(3-2-2-A)関数「exe_cy()」の【関数名】
「exe」は、英単語「execution」の省略形で「実行」を意味
「cy」は、「c」が英単語「center」で「中央」ですが、
ここでは、重心とし「y」で重心Y座標とします!
それで重心の計算を実行する関数です!
(3-2-2-B)関数「double exe_cy()」の【返値】
double TypeSf::exe_cy(void) // 重心Y座標算出
{倍精度浮動小数点数型で算出した重心座標を辺値とし返しま
す!
(3-2-2-C)関数「exe_cy()」の【仮引数】
存在しません!
(3-2-2-D)関数「exe_cy()」の【アルゴリズム】
{
if( a != 0 ){ // 面積が有効ならば
return( (double)mv / (double)a + (double)y - 1.0 ); // 左記で算出
}else{ // 面積が0なら
return( 0.0 ); // 0にする
} //
}if分岐条件「if(a!=0)」と面積≪クラスのメンバー変数
「int a;」≫が有効(≠0)ならば、分岐中身
「return((double)mv/(double)a+(double)y-1.0);」と
1次水平モーメント≪メンバー変数「float mv;」≫を式
「(double)mv/(double)a+(double)x-1.0」で面積で除算する
事で算出し「+(double)y-1.0」とフェレ始点からの相対座標
に補正!
(3-3)楕円情報の算出
(3-3-1)慣性主軸角の算出
☆備考☆この関数はファイル「TypeSf.cpp」に存在!
double TypeSf::exe_angle(void)
{
double mhhD; // 水平モーメント値
double mvvD; // 垂直モーメント値
double mhvD; // 相乗モーメント値
double mm; // 途中の値
double da; // Δa
double db; // Δb
double alD; // 慣性主軸角
da = -1.0e-20; // Δaをセット
db = -da; // Δbをセット
mhhD = mhh; // 水平Moment取出し
mvvD = mvv; // 垂直Moment取出し
mhvD = mhv; // 相乗Moment取出し
if( mhvD > da && mhvD < db ){ // 相乗=微少 ならば
if( mhhD >= mvvD ){ // 水平≧垂直の時
alD = 0.0; // 角=0.0にし
}else{ // 水平<垂直の時
if( mhvD >= 0.0 ){ // 相乗が正なら
alD = PAI / 2.0; // 角=π/2.0にし
}else{ // 相乗が負なら
alD = -PAI / 2.0; // 角= -π/2.0に
} // する
} //
}else{ // ≠0.0 なら
mm = ( mvvD - mhhD ) / mhvD; // 左記を計算し
if( mhvD < 0.0 ){ // 相乗Momentが負
alD = atan( ( mm - // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
}else{ // 相乗Momentが正
alD = atan( ( mm + // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
} //
} //
alD = -alD; // 角度の符号反転※注※
al = (float)alD; // 一旦保存
return( alD ); // 慣性主軸角を返す
}★注意★この関数は「public:」属性ですのでライブラリの
外から使用可能です!
(3-3-1-A)関数「exe_angle()」の【関数名】
「exe」は、英単語「execution」の省略形で「実行」を意味
「angle」は、「angle」が英単語「angle」で「角度」です
が、ここでは、幾何学的な項目とし慣性主軸角の計算を実行
する関数です!
(3-3-1-B)関数「double exe_angle()」の【返値】
double TypeSf::exe_angle(void)
{倍精度浮動小数点数型で算出した慣性主軸角を辺値とし返し
ます!
(3-3-1-C)関数「exe_angle()」の【仮引数】
存在しません!
(3-3-1-D)関数「exe_angle()」の
【ローカル変数】
{
double mhhD; // 水平モーメント値
double mvvD; // 垂直モーメント値
double mhvD; // 相乗モーメント値
double mm; // 途中の値
double da; // Δa
double db; // Δb
double alD; // 慣性主軸角「double mhhD;」は、メンバー変数「mhh」を関数内部で
使用する場合、レジスター等、より高速に動作する形に
コンパイラが割り付けると考え関数の内部でローカルに
セット
「double mvvD;」は、上記と同じ理由でメンバー変数
「mvv」をセットした変数
「double mhvD;」は、上記と同じ理由でメンバー変数
「mhv」をセットした変数
「double mm; 」は、計算途中の値
「double da; 」は、Δa、★備考Δは微小数値★
「double db; 」は、Δb、★備考Δは微小数値★
「double alD;」は、慣性主軸角度
(3-3-1-D)関数「exe_angle()」の
【アルゴリズム】
da = -1.0e-20; // Δaをセット
db = -da; // Δbをセット
mhhD = mhh; // 水平Moment取出し
mvvD = mvv; // 垂直Moment取出し
mhvD = mhv; // 相乗Moment取出し
if( mhvD > da && mhvD < db ){ // 相乗=微少 ならば
if( mhhD >= mvvD ){ // 水平≧垂直の時
alD = 0.0; // 角=0.0にし
}else{ // 水平<垂直の時
if( mhvD >= 0.0 ){ // 相乗が正なら
alD = PAI / 2.0; // 角=π/2.0にし
}else{ // 相乗が負なら
alD = -PAI / 2.0; // 角= -π/2.0に
} // する
} //
}else{ // ≠0.0 なら
mm = ( mvvD - mhhD ) / mhvD; // 左記を計算し
if( mhvD < 0.0 ){ // 相乗Momentが負
alD = atan( ( mm - // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
}else{ // 相乗Momentが正
alD = atan( ( mm + // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
} //
} //
alD = -alD; // 角度の符号反転※注※
al = (float)alD; // 一旦保存
return( alD ); // 慣性主軸角を返す
}「da=-1.0e-20;db=-da;」は、Δa・Δbと
「0に極めて近い」大小の範囲を定数としてセット!
「mhhD=mhh;mvvD=mvv;mhvD=mhv;」は、メンバー変数を
少しでも高速に成るローカル変数にセットして扱う?!
「if(mhvD>da&&mhvD<db){・・分岐中身・・}」は、条件
「(mhvD>da&&mhvD<db)」で2次相乗モーメント「mhvD」の
値が、Δa・Δbの間≒極めて0に近い値の場合の処理で
「if(mhhD>=mvvD){alD=0.0;}」は、2次水平モーメントが
2次相乗モーメント(水平×垂直)以上の場合が
「alD=0.0;」と角度を「0.0=水平方向角」にする!
「else{if(mhvD>=0.0){alD=PAI/2.0;}else
{alD=-PAI/2.0;}」は、条件「2次水平モーメントが
2次相乗モーメント(水平×垂直)依り小さい」となり、
その時が、
「if(mhvD>=0.0){alD=PAI/2.0;}else{alD=-PAI/2.0;}」と
更に内側ifで条件「mhvD>=0.0」と2次相乗モーメント
(水平×垂直)が有効なら、成立「alD=PAI/2.0;」と角度を
「ラジアン(π÷2.0)=ディグリー(90°)=垂直方向
角」にする!不成立「alD=-PAI/2.0;」と同じに成ります!
★備考★ワザワザ内側ifで成立/不成立と分けて居るのに
同じ事に成るのは、記載時は、取り敢えずコノ値にして後で
モット詳細に相応しい値にする心算だった筈ですが、作成か
ら30年近く経ち単にホッテ置いたかも知れません!
更に
★備考★外側ifで条件「(mhvD>da&&mhvD<db)」と2次
相乗モーメント(水平×垂直)が極小と言う特殊な条件の
場合で使用頻度が少ないと当時作者(私)は考えたと思え
る!
と言う訳で使用頻度の多い「else{・・処理・・}」の
処理「mm=(mvvD-mhhD)/mhvD;」と途中で数か所で使用される値を算出し、「if(mhvD<0.0)
{alD=atan((mm-sqrt(mm*mm+4.0))/2.0);}」とif条件
「mhvD<0.0」と2次相乗モーメント(水平×垂直)が
負(マイナス)の値なら
「atan((mm-sqrt(mm*mm+4.0))/2.0);」と逆正接≪
正接「tan()」の逆関数≫で角度を算出します!
★備考★何故、式の意味を解説シナイと訝しく思う人に!
言い訳的な説明≪元々、SPIDERと呼ばれる
50年近く前に編纂された画像処理言語FORTRANで
記載されたアルゴリズムコードをC言語に書き換えた物
です!但し、動作チェックは、
グラフィック描画関数『解説クラスGraphic○○』で
関数の説明を予定していますので乞うご期待と記載して
置きますが、その描画関数で楕円を描画し、
その図形を計測する事で検証しています≫!
そして「else{」とif条件「mhvD<0.0」が不成立の処理
「alD=atan((mm+sqrt(mm*mm+4.0))/2.0);}は、
「mm+sqrt()」と符号が±逆で算出し逆正接で角度を算出
します!
「alD=-alD;al=(float)alD;return(alD);」は、
辺値で返す前に符号反転しています!
★備考★一寸、前に記載した言い訳に動作チェックで
グラフィック関数で検証したと記載した事で判る様に
補正した跡です!
(3-3-2)等価楕円情報算出関数
☆備考☆この関数はファイル「TypeSf.cpp」に存在!
da = -1.0e-20; // Δaをセット
db = -da; // Δbをセット
mhhD = mhh; // 水平Moment取出し
mvvD = mvv; // 垂直Moment取出し
mhvD = mhv; // 相乗Moment取出し
if( mhvD > da && mhvD < db ){ // 相乗=微少 ならば
if( mhhD >= mvvD ){ // 水平≧垂直の時
alD = 0.0; // 角=0.0にし
}else{ // 水平<垂直の時
if( mhvD >= 0.0 ){ // 相乗が正なら
alD = PAI / 2.0; // 角=π/2.0にし
}else{ // 相乗が負なら
alD = -PAI / 2.0; // 角= -π/2.0に
} // する
} //
}else{ // ≠0.0 なら
mm = ( mvvD - mhhD ) / mhvD; // 左記を計算し
if( mhvD < 0.0 ){ // 相乗Momentが負
alD = atan( ( mm - // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
}else{ // 相乗Momentが正
alD = atan( ( mm + // 慣性主軸角算出
sqrt( mm * mm + 4.0 ) ) //
/ 2.0 ); //
} //
} //
alD = -alD; // 角度の符号反転※注※
al = (float)alD; // 一旦保存
return( alD ); // 慣性主軸角を返す
}★注意★この関数は「public:」属性ですのでライブラリの
外から使用可能です!
(3-3-2-A)関数「exe_oval()」の【関数名】
「exe」は、英単語「execution」の省略形で「実行」を意味
「oval」は、英単語「oval」の「楕円形」を意味です
が、ここでは、幾何学的な項目とし図形を楕円形と見なした
場合の慣性主軸角と長短両軸の径の計算を実行する関数で
す!
(3-3-2-B)関数「void exe_oval()」の【返値】返値を返さない関数です!
★注意★詰り、実引数の検査を実行時に行いませんので
使用する時は、正しい実引数を記載する必要が有ります!
(3-3-2-C)関数「exe_oval()」の【仮引数】
void TypeSf::exe_oval(
double& angle, // 角度:返値
double& r1, // 長径:返値
double& r2 // 短径:返値
){「double& angle,」は、楕円の角度≪傾きの角度≫
「double& r1,」は、長径≪長い方の直径≫
「double& r2」は、短径≪短い方の直径≫
★備考★「double&仮引数名」とポインタを経由して値を
返す事に注意して下さい!
(3-3-2-D)関数「exe_oval()」の【ローカル変数】
){
double sin_a; // sin(角度)
double cos_a; // cos(角度)
double mmajor; // 長径軸モーメント
double mminor; // 短径軸モーメント
double aD; // 面積「double sin_a;」は、sin(角度)
「double cos_a;」は、cos(角度)
「double mmajor;」は長径軸モーメント、
「double mminor;」は短径軸モーメント、
「double aD;」は、面積
(3-3-2-D)関数「exe_oval()」の【アルゴリズム】
angle = -exe_angle(); // 角度を取り出し※注※
sin_a = sin( angle ); // sin,cosを
cos_a = cos( angle ); // 算出
mmajor = mhh * sin_a * sin_a // 主軸モーメント
- 2.0 * mhv * cos_a * sin_a // を算出
+ mvv * cos_a * cos_a; //
mminor = mhh * cos_a * cos_a // 主軸と直交する
+ 2.0 * mhv * cos_a * sin_a // モーメントを算出
+ mvv * sin_a * sin_a; //
if( mmajor == 0.0 || mminor == 0.0 ){ // 軸Momentが0.0なら
r1 = 1.0; // 長径・短径の楕円
r2 = 1.0; // 相当を1.0にする
}else{ // 正常な値なら
aD = a; // 面積を取り出し
r2 = 2.0 * sqrt( sqrt( // 楕円の短径相当を
( aD * aD * mmajor ) // 算出
/ ( PAI * PAI * mminor ) ) ); //
if( r2 < 1.0 ){ // 短径が 1.0 未満
r2 = 1.0; // 1.0 に補正
} //
r1 = 4.0 * aD / ( PAI * r2 ); // 長径相当を算出
} //
angle = -angle; // 角度の符号反転※注※
}「angle=-exe_angle();」は、サブルーチン関数
「exe_angle()」で傾き角度を算出し仮引数「angle」に格納
「sin_a=sin(angle);」は、その角度でsin(サイン)の値
「cos_a=cos(angle);」は、その角度でcos(コサイン)の値
を算出して置く、
「mmajor=mhh*sin_a*sin_a-2.0mhv*cos_a*sin_a+
mvv*cos_a*cos_a;」は、長径軸モーメント算出
「mminor=mhh*cos_a*cos_a+2.0mhv*cos_a*sin_a+
mvv*sin_a*sin_a;」は、短径軸モーメント算出
「if(mmajor==0.0||mminor==0.0){r1=1.0;r2=1.0;}」は、
条件「mmajor==0.0||mminor==0.0」の場合が、長径・短径
の値を「r1=1.0;r2=1.0;」とセット!する特別な場合で
「else{・・中身・・}」は、通常の場合の処理と考えて
下さい!
そして中身、「aD=a;」は、クラスの
メンバー変数「int a;」を少しでも高速化の為に扱い易い
ローカル変数にセット!
「r2=2.0sqrt(sqrt((aD*aD*mmajor)/(PAI*PAI*mminor)));
」は、
「PAI」が、解説『エラーコード等各種単純定義』に説明
して有る「π≒3.14○○○○」で、関数「sqrt()」はC言語
標準「√」です!
「if(r2<1.0){r2=1.0;}」は、短径が「1.0」未満の時に
「1.0」にする補正です!
「r1=4.0aD/(PAI*r2);」は、長径を算出します!
★備考★何故、式の意味を解説シナイと訝しく思う人に!
言い訳的な説明≪元々、SPIDERと呼ばれる50年近く
前に編纂された画像処理言語FORTRANで記載された
アルゴリズムコードをC言語に書き換えた物です!
但し、動作チェックはグラフィック描画関数
『解説クラスGraphic○○』で関数の説明を予定して
いますので乞うご期待と記載して置きますが、その描画関数
で楕円を描画し、その図形を計測する事で
検証しています≫!
2.構造体「struct TypeMB構文で定義」した!サブセットメンバー変数の定義概要
struct TypeMB
{
short x; // フェレ始点x座標
short y; // フェレ始点y座標
short h; // 水平フェレ径
short v; // 垂直フェレ径
short xl; // ラベル始点のx座標
int len; // 周囲長
int a; // 面積
};「x・y・h・v・x・len・a 」は、
クラス「TypeSf構文で定義」した!
メンバー変数と同じです!
何故、これが、存在するかと言うと、
クラス「TypeSf構文で定義」での図形計測結果を
格納すると大きく成り、極一般的に多く使用頻度の
高いメンバー変数に特化したコンパクトなデータ構造を
用意した心算です!
解説『解説クラスFilter(○○』等で解説する
図形計測関数関数「MeasureFere()」等は、
多重定義(オーバーロード)関数として
クラス「TypeSf構文で定義」した結果データ格納も、
構造体「struct TypeMB構文で定義」した
結果データ格納も両方使用可能な関数に大部分が、
成っています!
★備考★ここで「MB」名称は、
「M」が「measurement」の略詰り、計測を意味し、
「B」が「base」の略で基本部を意味、
「Sf」は、「S」が何で有ったか、今と成っては、
思い出せません、「f」は、
多分「Figure measurement」図形計測からと思えます!
解説『解説クラスFilter(○○』は、
今年(2024)年中には発表出来る筈ですので乞う
ご期待と記載して、このクラス「TypeSf構文で定義」の
解説を完了します!
★備考★
解説『解説クラスTypeArray』でも記載したが、
noteエディタの変な特性でコピペした文章の半角「*」
が消されたり、空白「 」が消される事が多々あります!
注意して手作業で修正している筈ですが、必ず、code
機能で表示して居る物を正しいとして確認して下さい
☆次は、解説『解説クラスCopyClear(○○)』
続講しますので御贔屓の程、宜しくお願い致します。
