デジモンアドベンチャー 第5話電光!カブテリモンに登場するプログラム
本編
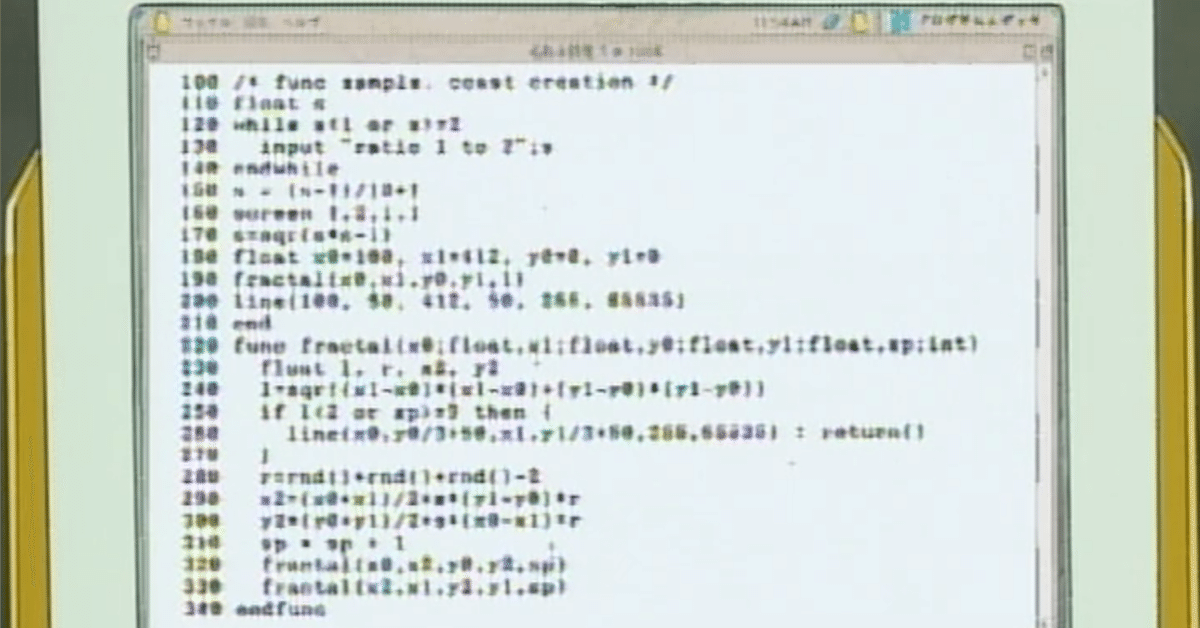
次のようなコードを見つけました。
(読みやすさのために順番を変えてる箇所があります)
/* func sample. coast creation */
float s
while s<1 or s>=2
input "ratio 1 to 2";s
endwhile
screen 1,2,1,1
line(100, 50, 412, 50, 255, 65535)
s = (s-1)/10+1
s=sqr(s*s-1)
float x0=100, x1=412, y0=0, y1=0
fractal(x0,x1,y0,y1,1)
end
func fractal(x0:float,x1:float,y0:float,y1:float,sp:int)
float l, r, x2, y2
l=sqr((x1-x0)*(x1-x0)+(y1-y0)*(y1-y0))
if l<2 or sp>=9 then {
line(x0,y0/3+50,x1,y1/3+50,255,65535) : return()
}
r=rnd()+rnd()+rnd()-2
x2=(x0+x1)/2+s*(y1-y0)*r
y2=(y0+y1)/2+s*(x0-x1)*r
sp = sp + 1
fractal(x0,x2,y0,y2,sp)
fractal(x2,x1,y2,y1,sp)
endfunc言語は実在するもので、"X-BASIC"というものらしいです。
X-BASICは、シャープX68000用にハドソンおよびシャープが開発したBASIC言語である。
特徴としてはC言語に似た独自の構文をもった構造化言語であり、他の多くのBASICとは似ていないという印象が強い。一般にBASICには大文字を基本としているものが多いが、小文字を使うのも特徴である。
おそらく何らかのフラクタルを再帰的に描画するプログラムっぽいので、pythonにて書き直してみました。これです。
import matplotlib.pyplot as plt
from random import random as rnd
from random import uniform
from math import sqrt as sqr
def main():
# 初期設定
plt.figure(figsize=(10, 5))
plt.title(" ")
# 初期の直線
x_start, y_start = 100, 0
x_end, y_end = 412, 0
fractal(x_start, y_start, x_end, y_end, 1)
plt.hlines(y=0, xmin=100, xmax=412, color="blue", linewidth=1)
plt.axis("off")
plt.show()
def fractal(x0, y0, x1, y1, sp):
"""
x0, y0: 線分の始点座標
x1, y1: 線分の終点座標
sp: 再帰の深さ
"""
s = uniform(1, 2)
s = ((s - 1) / 10) + 1
s = sqr(s * s - 1)
# 線分の長さを計算
l = sqr((x1 - x0) ** 2 + (y1 - y0) ** 2)
# 線分が閾値以下 or 再帰の深さが一定以上なら終了
if l < 2 or sp >= 9:
plt.plot([x0, x1], [y0, y1], color="blue", linewidth=1)
return
x2 = (x0 + x1) / 2 # 中点X座標
y2 = (y0 + y1) / 2 # 中点Y座標
r = rnd() ** 3 - 2
offset_x = s * (y1 - y0) * r
offset_y = s * (x0 - x1) * r
x2 += offset_x
y2 += offset_y
fractal(x0, y0, x2, y2, sp + 1)
fractal(x2, y2, x1, y1, sp + 1)
if __name__ == "__main__":
main()結果はこんな感じになりました。
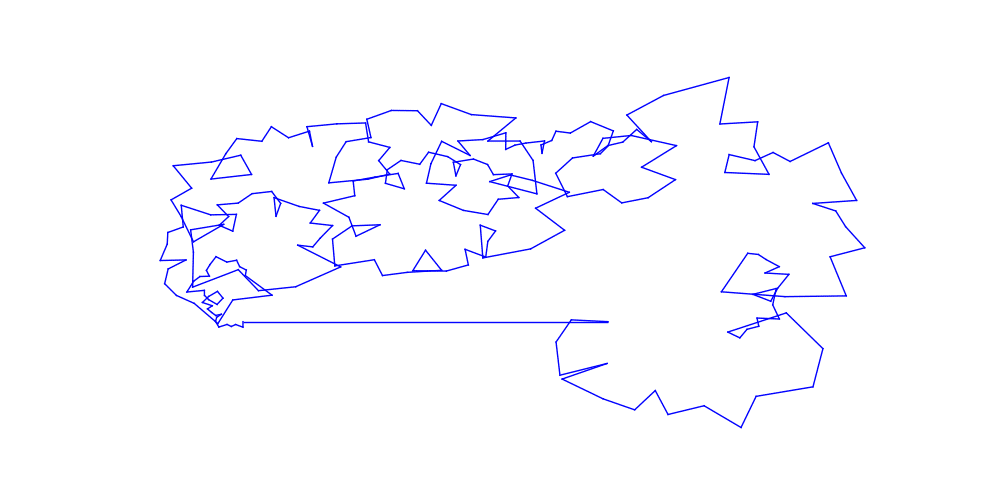
シード値によっていろんな図形が完成します。これとか。

きれいですね。
おまけ
生成の仕組みを覗いてみましょう。これが正解かどうかはわかりません・・・
さきほどのプログラムの中で、フラクタルの生成に関係する部分を抜粋します。
def fractal(x0, y0, x1, y1, sp):
"""
x0, y0: 線分の始点座標
x1, y1: 線分の終点座標
sp: 再帰の深さ
"""
# シード値には1 <= x <= 2 を満たす乱数を利用
s = uniform(1, 2)
s = ((s - 1) / 10) + 1
s = sqr(s * s - 1)
# 線分の長さを計算
l = sqr((x1 - x0) ** 2 + (y1 - y0) ** 2)
# 線分が閾値以下 or 再帰の深さが一定以上なら終了
if l < 2 or sp >= 9:
plt.plot([x0, x1], [y0, y1], color="blue", linewidth=1)
return
x2 = (x0 + x1) / 2 # 中点X座標
y2 = (y0 + y1) / 2 # 中点Y座標
r = rnd() ** 3 - 2
# "ズレ"を計算
offset_x = s * (y1 - y0) * r
offset_y = s * (x0 - x1) * r
x2 += offset_x
y2 += offset_y
fractal(x0, y0, x2, y2, sp + 1)
fractal(x2, y2, x1, y1, sp + 1)
初期状態として、2点$${P,Q}$$の座標とそれを結んでできる線分$${PQ}$$を与えます。こんな感じです。

終了条件のために、$${PQ }$$の長さ$${ l=\sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2}}$$を求めておきます。$${l < 2}$$となったら再帰は終了です。
次に$${PQ}$$の中点$${M}$$の座標$${x_{2}, y_{2}}$$を$${x_2 = \frac{x_0 + x_1}{2}}$$,$${y_2 = \frac{y_0 + y_1}{2}}$$という感じで求めます。まあこんな感じです。

次に$${\text{offset}\_x, y}$$ですが、これは点$${M}$$をどれだけずらすかということなので、式の形自体はあまり重要ではないです。とにかくある一定量ずらすよ〜〜というモチベーションの量です。プログラムの方では、シード値$${s}$$と乱数$${r}$$を用いて、
$$
\text{offset}\_x = sr(y_1 - y_0) \\
\text{offset}\_y = sr(x_1 - x_0)
$$
と定めてあります。これらをそれぞれ$${x_2, y_2}$$に足して、新たな点$${R (x_2 + \text{offset}\_x, y_2 + \text{offset}\_y)}$$をつくります。こんな感じです。

線分$${PR}$$と$${QR}$$についても同様の操作を行なっていくことにより、冒頭のフラクタルが得られるという仕組みです。
ちなみに、コメントの /* func sample. coast creation */からわかるように、この流れは海岸線のフラクタルを与えるものになっています。

追記
2025/02/24
図を綺麗にした
