同じことを1万回やってみる
ランダムに起こっていそうなことから、その結果どうなるのかを観察したいときには、それを何千回か何万回かやってみればよいです。例えば、先の回では「さいころを100回振ったら3の目が何回出るか」というランダムに起こっていそうなことを1万回繰り返して集計しました。最後に理論的な背景と、実はその数字が分布関数ですぐに出せるよって言うところまで説明しましたが、現実の問題で理論式がすぐに導ける単純な事柄はまれです。
統計の世界は、様々な問題セッティングについてその理論式を作っていく学問なので(実はそれだけではないですが、今の流れでは)、データサイエンティストたちは与えられた問題をうまいこと統計の枠組みに乗せて、理論式(~モデル)を組み立て、結論に結びつけます。一方で、先の記事でやったように、理論式(ここでは二項分布)を知らなくても、何万回もやってみればいいじゃん、っていうのがこのExcelシミュレーションシリーズです。
問題例:クラスに誕生日が同じな生徒がいる確率
こういう問題が出たとき、データサイエンティストはこれを数理的、論理的に計算する方法を考えます。例えばクラスが40人として、二人が1/365の確率で同じ誕生日である確率は何%か。そして、それがクラスのすべての2名組で起こるとすると、全体で何%か、などなど。これ自体はおそらく高校数学レベルの問題だと思うので、理系なら解析的に解ける人も多いと思いますが、ここはシミュレーションの練習なので、シミュレーションで求めてみます。
ひとりに注目
まずは一人に注目します。誕生日は完全にランダムで決まるとしましょう。実は、誕生日の分布には若干偏りがあるのですが、今回は無視します。一つのセルにひとりの誕生日をランダムで記入するとすれば、セルに入れる関数は
=INT(RAND()*365)です。これで、一つのセルに0~364の整数が同じ確率で与えられます。
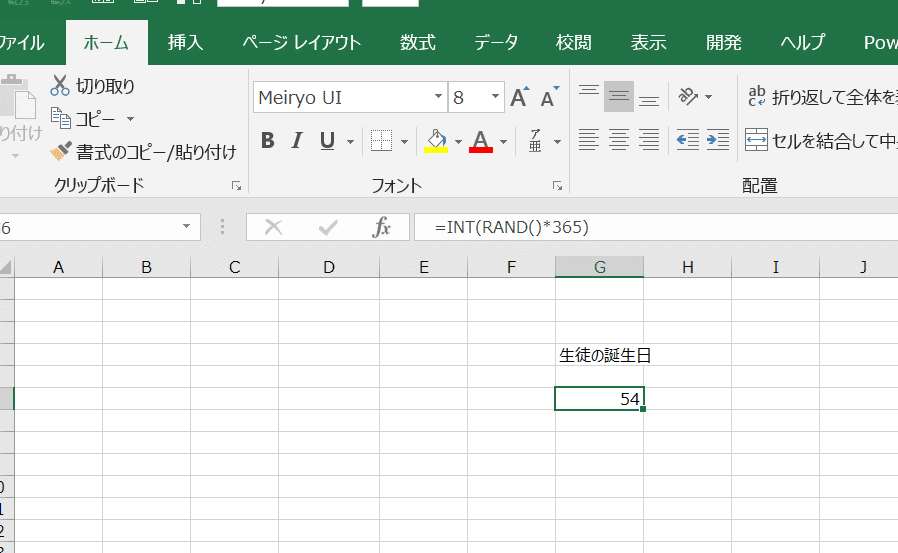
ただ、0~364の数字ですとあまり誕生日っぽくないので、例えば今の6年生のクラスを想定して、2011/4/2=39540を足してセルの表示形式をmm/ddにしておきます。
クラスに注目
次はクラスを作ります。クラスの人数は40人とすると、この一人分を40セルにコピーします。わかりやすいように上に出席番号を1から40まで記入して、その下に誕生日番号を入れます。

これで、1クラス分の誕生日ができました。[F9]を押せば誕生部が変わります。
ここで、今回知りたいのは、クラスに同じ誕生日の人がいる確率ですから、この中に同じ値が存在するかどうかを調べなければなりません。そこで、調べる関数を書きましょう。いろんな方法がありますが、今回はCOUNTIFを使ってみます。
あとでこのクラスを下方向に1万クラス分コピーしたいので、同じ人がいるかどうかのチェックは横に繋げます。今、AT6まで誕生日が入っているので、その横に、出席番号1番から順に、「私と同じ誕生日の人数」を書いていきます。AU6に入れる関数は、
=COUNTIF($G6:$AT6,G6)-1です。$G6:$AT6はクラスの出席番号1番から40番までの人の誕生日を示しており、それが自分の誕生日=G6と同じかどうかを調べています。-1は自分をカウントした分を除いています。これを横方向にCH6までコピーしていくと、$G6:$AT6の方は変わらず、G6だけが相対参照で変わっていくので、それぞれの生徒の誕生日を、クラス全員の誕生日と比較することになります。
最後に、こうして数えた「同じ誕生日の人の人数」を総和して1を超えていれば、誰かが同じ誕生日であることが分かるので、
=IF(SUM($AU6:$CH6)>0,1,0)をE6に入れます。=SUM($AU6:$CH6)>0 にして、TRUE/FALSEで表示してもいいのですが、あとで平均を取りたいので、同じ誕生日の人が{1=いる、0=いない}、にしておきます。
これで、クラスに同じ誕生日の人がいるかどうかの判定ができるようになりました。[F9]を押すと再計算されて、誕生日がくるっと変わりますので、[F9]を何度も何度も押してみると、判定が0か1かがどのくらいの確率で出てくるかが分かると思います。実際にやってみると、高い確率で1、つまり、誰かが同じ誕生日であることが分かると思います。
クラスを沢山作る
すると、さらに知りたくなるのは、具体的にどのくらいの確率で同じ誕生日が発生しているか、ですね。そこで、今作ったセルを、下方向に沢山コピーします。1クラス分のシミュレーションは完結しているので、これを下方向にコピーすれば、クラスがたくさんできることになります。今日は表題通り一気に1万行までコピーしてみます。かなり時間がかかりますので、ゆっくり待ちます。
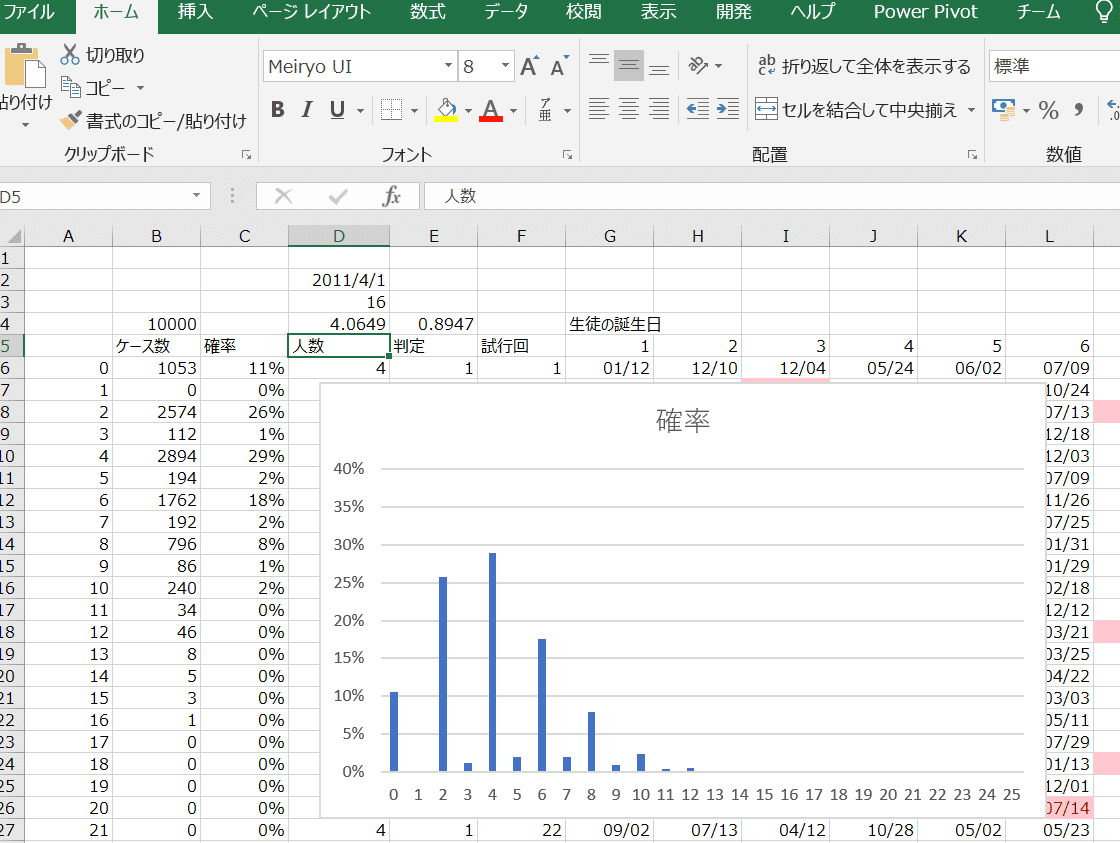
その後、E列には0か1かが入っていますので、これを全部選択してAVERAGEをとると、「同じ誕生日がいる人の確率」が出てきます。およそ89%くらいであることがわかりますね。40人のクラスでは、かなり高い確率で同じ誕生日の人がいることがわかります。
さらに興味が湧いたら、例えば同じ誕生日である人が何人いるかを数えて平均を取ってみると、平均4人はいることがわかったり、その分布をとってみると6人、8人いることも8%程度と、そんなにレアではないことだってこともわかります。
おわりに
以上のように、最初に一人に注目し、その次にクラスに注目し、最後にそれを沢山作って確率を求めました。Excelを使ってシミュレーションする利点の一つは、最初から大きな構成を考えるのではなくて、注目するところをだんだんと大きくする、最初に注目したいところを作って観察し、それを使って気がついたこと、気になったことをもう少し大きくしてまた観察し、さらに大きくして観察する、という順で、個々を観察しながら思考範囲を広げていけるところです。Rなどのプログラミング言語などを使うと、それなりに全体構成を考えてから始める必要があったり、個々の事象を観察するのに少しハードルが高かったりします。反面、Excelでは融通が利かないところも多くて、例えばクラスの人数を40人から30人に変更しようとするとExcelでは結構面倒だったりしますが、プログラミング言語ではN=40をN=30に変更するだけかもしれません。Excelでちゃちゃっとやってみて、見通しをつけてから、プログラミング言語で作り直す、といった使い方も便利です。
