Excelでシミュレーション
集計可視化の話は「うごくExcel」でおよそ終わりで、次のお題はシミュレーションです。
シミュレーションとは
シミュレーションとは、何らかの「システム」があり、そこへ「制御」を加えたときに、システムの挙動をコンピューター上で再現することです。例えばフライトシミュレーションゲームは、飛行機が動くというシステムがあって、そこに操縦という制御を加えると、どのように動くか、つまり、姿勢がどう変化して、どこへ飛んでいくか、という挙動になります。シムシティも、都市が成長するルール=システムがあり、そこに、「何にどれだけ投資するか」という制御を加えると、都市が成長します。
統計寄りでは。例えば六面体のサイコロがあったときに、どの目がどれだけ出るかをシミュレーションできます。このとき、システムは「サイコロを振るとランダムに1~6の面が出る」、制御は「サイコロを振る」、挙動の結果は、「どれかの目が出る」です。
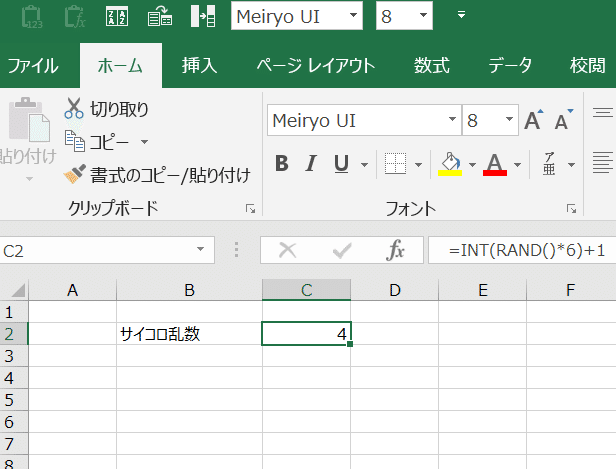
Excelのセルに、つぎの式を入れます。
=INT(RAND()*6)+1すると、このセルは六面体サイコロになります。数式を入れた瞬間に、1~6の値になると思いますが、どの値になるかは決まっていません。そして、Excelを「再計算」すると([F9]を押すと再計算されます)値が変わります。1になったり、2になったり、・・・しかし、0以下にはなりませんし、7以上にもなりません。さらには、何度も繰り返し再計算してみると、1~6の値が均等に出てきているような気がします。これが、サイコロのシミュレーションです。
繰り返しシミュレーション
さて、上では[F9]を何度も何度も押して、再計算を繰り返しました。100回[F9]を押せば、100回分の値が取れます。では、どの目が何回出たでしょうか?
[F9]を押して出た目をノートに一つずつ記録していけば、100回再計算してどの目が何回出たかがわかります。が、それはかなり大変。では、VBAマクロを利用して、再計算と記録を繰り返す・・・のも、VBAを書くのが面倒です。
そこで、上の計算式をコピーして100セル分ペーストします。すると・・・

これらのセルの中にはすべて、先ほどと同じ数式が入っています。そして、値がそれぞれ異なります。100セル分ペースとしたので、これは100回シミュレーションをしたのと同じになります。では、その100回のうち、それぞれの値は何回ずつ出たでしょうか?
以前にやったヒストグラムを作ればいいですね。
=COUNTIF($C$2:$C$101,E3)そして、これを1~6まで並べて棒グラフにすると、
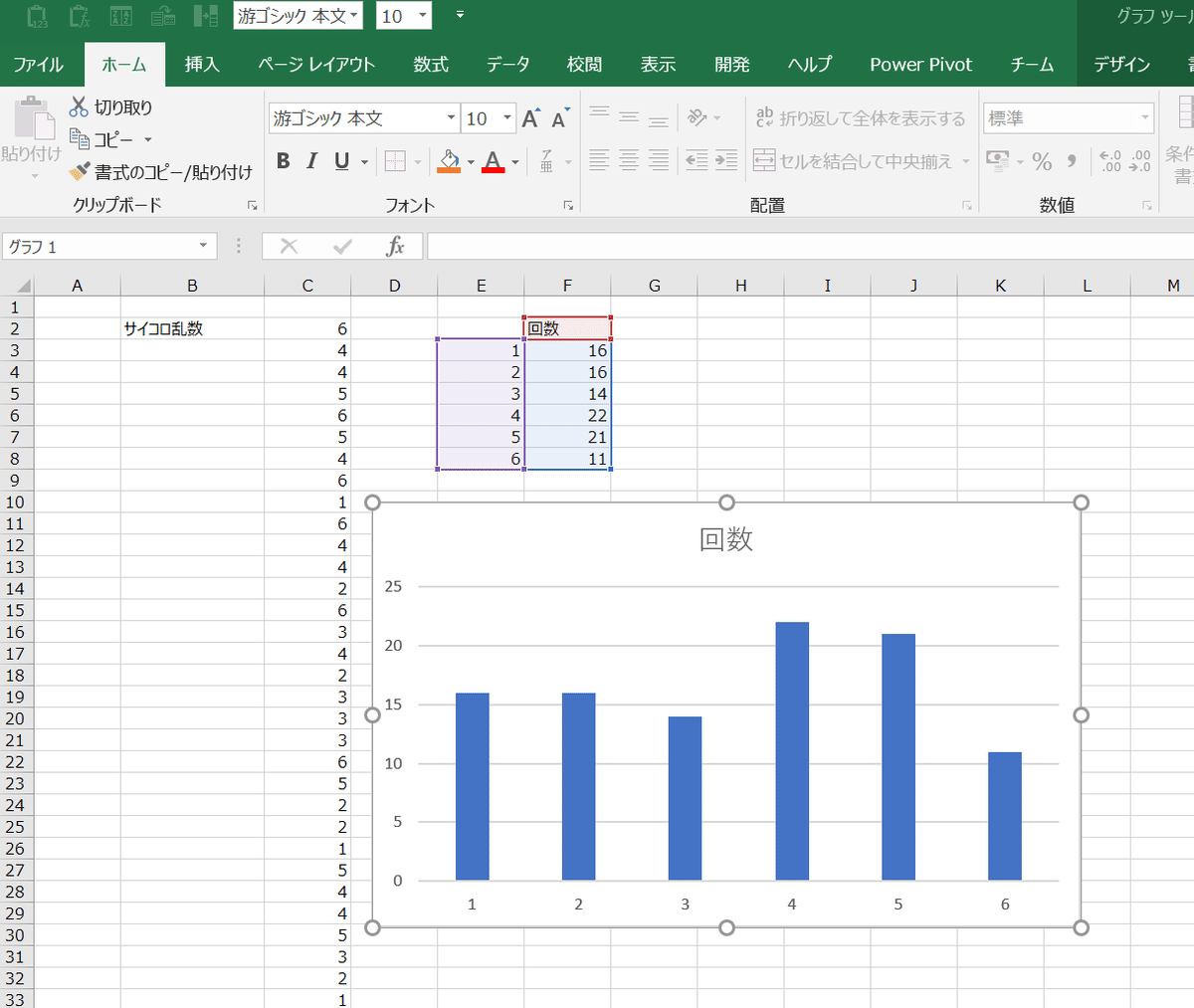
こんな感じになります。出た目の回数にかなりブレがありますね。正しいサイコロでしたら、100回振れば18回前後になるはずですが、3が14回、4は22回出ています。このサイコロはイカサマのようですね。
と思って[F9]を押すと、また変化しました。何度も何度も[F9]を押して再計算すると、各目の出る回数は大きく変化します。多くなったり少なくなったりして、必ず3が小さいとか、4が大きいわけでも無さそうです。では、各目の出る回数、例えば3の出る回数の変化はどのくらいなのでしょうか。
繰り返しシミュレーションの繰り返しシミュレーション
上では、1セルに入ったサイコロを100セル分にペーストすることで、100回分のサイコロにしました。そして今、「100回分のサイコロのうち3の出る回数」の変化を知りたい。ということは、1回分を100セルペーストしたように、100回分を100列にペーストすれば、3が出る回数の傾向を観察することができます。

このサンプルでは、N7から縦方向に100セルのサイコロをペーストし、それをさらに列方向に100列ペーストしました。合計、1万セル分のサイコロがあります。そして、N4から横に、各列で3の出た回数を数えています。1列目(N4)の関数は
=COUNTIF(N$7:N$106,3)です。ちなみに、これを横方向にペーストしていくと、式の中のNの場所がペーストに合わせて横方向にドリフトするので楽です。Excelのワークシートを作る際には、この絶対参照($付き、コピペしても動かない)と相対参照($なし、コピペすると一緒に動く)をうまく活用して、式を簡単にコピペできることを心がけます。式を書くセルは1つで、これを縦横にペーストするだけにしておけば、式のメンテナンスも簡単ですし、なによりエラーが混入しにくいです。
そして、C5に入っている式は、
=COUNTIF($N$4:$DI$4,B5)です。サイコロの目を数え上げた結果を、さらに数え上げます。すると、100回サイコロを振って3が出る回数のヒストグラムを書くことができます。これも[F9]で再計算すると変化します。
・・・100回程度ですと、かなり激しく動きますね。では、列を1000列に増やすと、

かなり落ち着いてきました。16回程度が真ん中で、しかし、5回しか出なかったり、31回も出たりすることもあるようです。さらに増やしてみましょう。

1万列にすると、もう分布の形はかなりきれいな釣り鐘状になりました。平均を
=SUMPRODUCT(B5:B45,C5:C45)/C3で計算すれば(B5:B45は3の出た回数で、C5:C45はその出た回数が現れた列数、C3は全体の回数)、16.7程度で落ち着いています。つまり、3が出る回数の期待値は100回中16.7回程度、しかし、6回程度で終わる場合もあれば、30回近くまでいくこともある、ということが分かりました。
実は、サイコロを振っている式は、6つの全ての面が均等に出現するように作られていますので、3の目が出る確率は1/6=0.167程度になります。しかし、100回繰り返しサイコロを振る程度では、そのうちで3が出る回数はかなりばらつくということが分かりました。
確率統計の理論から、二項分布と比較
なお、確率統計をやったことがあれば、この分布は「二項分布」であることがすぐにわかるとおもいます。試行回数100回、成功確率が1/6の時の、成功回数の分布を示すのが、二項分布です。Excelにも二項分布の関数があるので、これを横に並べて書いてみますと(B5は回数の参照、100はサイコロを振る回数、1/6は3の出る確率、$C$3は列数)、
=BINOM.DIST(B5,100,1/6,FALSE)*$C$3
このように、ほぼ一致することがわかります。右の方で100×1万=100万個のサイコロを使ってシミュレーションした結果と、確率統計の理論から作成した二項分布とが一致したことが観察できたと思います。
