
量子テレポーテーション
SFの世界の話ではなくて、量子コンピューティングのお話です。ある量子ビットが任意の量子状態にある時、その状態を別の量子ビットに転送する方法です。なんか量子テレポーテーションってかっこいいので、キャプションの画像はAIにお願いして作ってもらいました。
任意の状態の量子ビットはコピーできない
古典ビットはコピーできますが、任意の状態の量子ビットはコピーできません。
もしそのような操作ができるユニタリ演算子があったと仮定すると、
$${U_{c}(\ket{\psi}_{A}\ket{0}_{B})=\ket{\psi}_{A}\ket{\psi}_{B}}$$
$${U_{c}(\ket{\phi}_{A}\ket{0}_{B})=\ket{\phi}_{A}\ket{\phi}_{B}}$$
が成り立ちます。
2つの式の右辺同士、左辺同士で内積をとると、
$${\bra{\psi}_{A}\bra{\psi}_{B}\ket{\phi}_{A}\ket{\phi}_{B} = (\braket{\phi|\psi})^{2}}$$
$${(\bra{\psi}_{A}\bra{0}_{B}U_{c}^{\dag}U_{c}\ket{\psi}_{A}\ket{0}_{B}) = \braket{\phi|\psi}}$$
この2式は同じなので、$${\braket{\phi|\psi}^{2} = \braket{\phi|\psi}}$$となり$${\braket{\phi|\psi}}$$は任意の値を取れなくなるので矛盾することがわかります。
では、コピーできないのに任意の量子状態の量子ビットをどうやって転送するのでしょうか。
量子テレポーテーション
実はコピーができなくてもシンプルな量子回路を組むだけで、任意の量子状態を転送することができます。その名も量子テレポーテーション。
では早速そのやり方を見てみましょう。
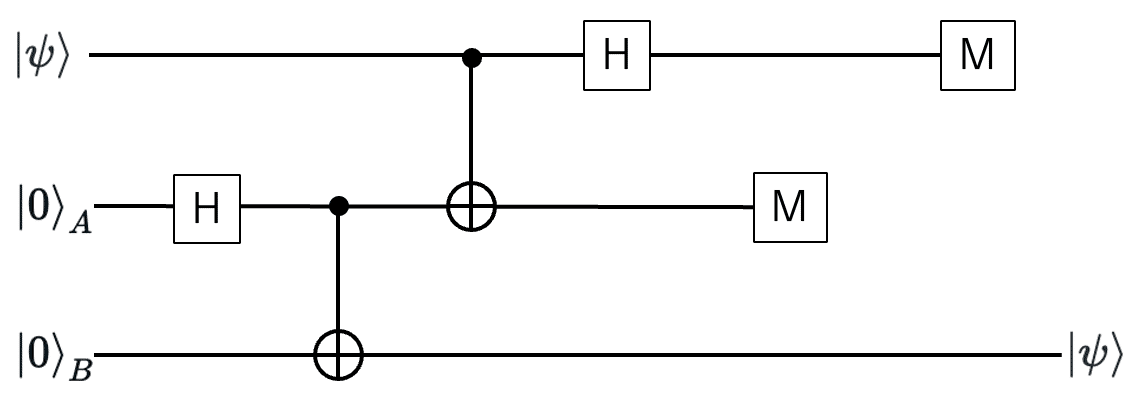
量子回路はシンプルです。一番上からメッセージビット、Aビット、Bとビットとします。順番に見ていきましょう。
メッセージビットは任意の量子状態なので
$${\ket{\psi} = \alpha\ket{0} + \beta\ket{1}}$$
まずA,Bの量子ビットをもつれさせます。
量子ビットAにアダマールゲートを作用させた後に、CNOTゲートを作用させます。これでA,Bでもつれの状態になります。
$${\ket{Bell}_{A,B} = \frac{1}{\sqrt{2}}(\ket{00} + \ket{11})}$$
これにメッセージビットも加えて
$${(\alpha\ket{0} + \beta\ket{1}) \frac{1}{\sqrt{2}}(\ket{00} + \ket{11})}$$
$${= \frac{1}{\sqrt{2}}(\alpha\ket{000} + \alpha\ket{011} + \beta\ket{100} + \beta\ket{111})}$$
CNOTを作用させ
$${\frac{1}{\sqrt{2}}(\alpha\ket{000} + \alpha\ket{011} + \beta\ket{110} + \beta\ket{101})}$$
アダマールゲートを作用させます。式をまとめると。
$$
\frac{1}{2}(\alpha\ket{000} + \alpha\ket{011} + \alpha\ket{011} + \alpha\ket{111} + \beta\ket{010} - \beta\ket{110} + \beta\ket{001} - \beta\ket{101})
$$
さて、この状態でメッセージビットとAビットを測定します。
両方とも0が観測された場合
$${\ket{00}(\alpha\ket{0} + \beta\ket{1})}$$
このBビットの状態はまさにメッセージビットの最初の状態になっています。
01が観測された場合
$${\ket{01}(\alpha\ket{1} + \beta\ket{0})}$$
この場合はBビットにXゲートを作用させることでメッセージビットの最初の状態となります。
$${\ket{01}(\alpha\ket{0} + \beta\ket{1})}$$
10が観測された場合
$${\ket{10}(\alpha\ket{0} - \beta\ket{1})}$$
この場合はBビットにZゲートを作用させて位相を反転します。
$${\ket{01}(\alpha\ket{0} + \beta\ket{1})}$$
11が観測された場合
$${\ket{11}(\alpha\ket{1} - \beta\ket{0})}$$
この場合はXゲートを作用させてからZゲートを作用させることでメッセージビットの状態まで持っていくことができます。
$${\ket{01}(\alpha\ket{0} + \beta\ket{1})}$$
このようにメッセージビットとAビットの観測結果によってBビットに作用させるゲートを変えることで、見事にBビットにメッセージビットの状態を転送することができました!
