ニューラルネットワークの覚書
ニューラルネットワークを理解したくて遊んだ記録です。
基本構成
以下の構成で、ニューラルネットワークの動作原理について確認した記録です。
入力ノード、中間ノード、出力ノードからなる2層のニューラルネットワークとする
各ノードは、列ベクトル(縦ベクトル)とする
学習データ、教師データは、1件分を1行とする2次元行列とする
学習データは、仮想のデータを作成する
ニューラルネットワークは、pythonのクラスとして実装する
回帰
回帰に使用するニューラルネットワーク
中間ノードの活性化関数は ReLU
出力ノードの活性化関数は恒等関数
誤差関数は平均2乗和誤差
ニューラルネットワークのクラス
import numpy as np
# ニューラルネットワークのクラス定義
# NN(入力ノード、隠れ層ノード、出力ノード、学習率)
# w1,b1 1層目(入力と隠れ層の間)
# w2,b2 2層目(隠れ層と出力層の間)
# test(input_data) 学習済みの実行
# learn(input_data,train_t) 学習
# 引数
# input_data , train_t 2次元のndarray(列ベクトル)で処理
class NN:
def __init__(self,nn_in,nn_hid,nn_out,learn_r):
self.inodes=nn_in
self.hnodes=nn_hid
self.onodes=nn_out
# 重みパラメータ。-0.5 〜 0.5 でランダムに初期化。
self.w1 = np.random.rand(self.hnodes, self.inodes) - 0.5
self.w2 = np.random.rand(self.onodes, self.hnodes) - 0.5
self.b1 = (np.random.rand(self.hnodes) - 0.5).reshape(self.hnodes,-1)
self.b2 = (np.random.rand(self.onodes) - 0.5).reshape(self.onodes,-1)
# 学習率
self.learn_rate=learn_r
# 活性化関数は ReLU
self.activation=lambda x: np.maximum(0, x)
# 活性化関数の微分
self.activation_dash=lambda x: (np.sign(x) + 1) / 2
# 出力層の活性化関数は恒等関数なので関数はなし
pass
# 勾配の計算 1バッチ分 引数は複数データ
def q_diff(self,X,T):
r,c=self.w1.shape
delta_w1=np.zeros(r*c).reshape(r,c)
r,c=self.b1.shape
delta_b1=np.zeros(r*c).reshape(r,c)
r,c=self.w2.shape
delta_w2=np.zeros(r*c).reshape(r,c)
r,c=self.b2.shape
delta_b2=np.zeros(r*c).reshape(r,c)
for xx,tt in zip(X,T):
# 1件分のデータを入力したときの各ノードでの出力
xx=xx.reshape(-1,1)
tt=tt.reshape(-1,1)
h1_out,out=self.forward(xx,1)
# 出力層の誤差
e_out=out-tt
# 隠れ層の誤差
# dif @ w2(e_out-->行ベクトル)、w2.T@e_out(e_out-->列ベクトル)
h_err = self.activation_dash(self.w1@xx) * (self.w2.T@e_out)
# 勾配の平均(または合計)の総和
n=X[0,:].size
delta_w1+=h_err@xx.T / n
delta_b1+=h_err / n
delta_w2+=(e_out@h1_out.T ) / n
delta_b2+=e_out / n
return delta_w1,delta_b1,delta_w2,delta_b2
# 順方(学習結果の利用)引数は1データ
def forward(self,x,ck=0):
x=x.reshape(-1,1)
h1_out=self.activation(self.w1 @ x + self.b1)
out=self.w2 @ h1_out + self.b2
if ck==0:
return out #self.w2 @ self.activation(self.w1 @ x + self.b1) + self.b2
else:
return h1_out,out
# 逆方向(学習) 引数は複数データ
def backward(self,X, T):
delta_w1,delta_b1,delta_w2,delta_b2=self.q_diff(X,T)
# 重みの更新(学習)
self.w1 -= self.learn_rate * delta_w1
self.b1 -= self.learn_rate * delta_b1
self.w2 -= self.learn_rate * delta_w2
self.b2 -= self.learn_rate * delta_b2
pass
# 問い合わせ
# 順方向(1件分のデータ)
def test(self,input_data): # 中間層出力の返り値なし。学習中はforward(self,x,ck=1)で利用
return self.forward(input_data)
# 逆方向(学習) 入力データは複数データ(バッチサイズのデータ)
def learn(self,input_data,train_t):
return self.backward(input_data,train_t)
# 勾配計算のデバッグ用 (q_diffは学習で利用)
def diff(self,input_data,train_t):
return self.q_diff(input_data,train_t)
pass2入力、1出力の回帰用ニューラルネットワーク(2数の足し算)
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from matplotlib import gridspec
from mpl_toolkits.mplot3d import Axes3D
# 動作確認
# NNの構成
nn_in = 2 # 入力ノード数
nn_out = 1 # 出力ノード数
nn_hidden = 1024 # 隠れ層のノード数
learn_rate=0.0001
nn=NN(nn_in,nn_hidden,nn_out,learn_rate) # NNのオブジェクト生成
# 訓練データ
#========================ここにデータ生成又は読み込みを
train_count = 200 # 訓練データ数
# 一様乱数でデータ生成
np.random.seed(seed=1) # 動作確認の間、乱数を固定した(NNのデバッグ時)
rng = np.random.default_rng()
r = rng.uniform(-10, 15, (train_count,2))
x1 = r[:,0].reshape(train_count,1)
x2 = r[:,1].reshape(train_count,1)
x=np.hstack([x1, x2]) # X1、X2を結合
t=np.array([])
for i in range(x1.size):
# ここの式で回帰させたい関数を設定(教師データ)
f=1*x1[i,0]+1*x2[i,0] + rng.uniform(-0.5, 1.0)
t = np.append(t,f)
t=t.reshape(-1,1)
#========================
epoch=500
# バッチサイズ
# bach_size=1 # オンライン確率的勾配降下法(SGD)
bach_size=10 # バッチサイズ10のミニバッチSGD
# bach_size=train_count # 勾配降下法(全データ利用)
# train_countで収束しない ===========<<<<<このエラーを修正
# 学習率を修正(小さく)することで収束した
# バッチサイズのデータに分割
bach_n=(train_count+bach_size-1)//bach_size # 1エポックに必要なバッチ処理回数
print('1エポックあたりのミニバッチ数=',bach_n)
index=np.arange(train_count) # 確率的勾配降下のバッチ処理用
e_sum=np.array([]) # 1エポックごとの平均2乗和誤差
# 学習の開始
for i in range(epoch):
# 1エポックごとにデータをシャッフルし、ミニバッチデータを作成
np.random.shuffle(index) # インデックスをシャッフル
n=list(range(bach_size,train_count,bach_size)) # 例 [20, 40, 60, 80] 分割する位置の生成
index_split=np.array(np.split(index, n)) # 分割されたインデックスの2次元配列
# bach_n 回で、1エポック分の処理
flg=False # 2重ループを抜けるためのフラグ
for j in range(bach_n):
# 分割されたインデックスに該当するデータ
x_bach=x[index_split[j]]
t_bach=t[index_split[j]]
nn.learn(x_bach,t_bach) # 学習<<<<<------------------------
# 更新ごとの平均2乗和誤差の計算
e=np.array([])
for xx,tt in zip(x,t):
e=np.append(e,(nn.forward(xx)-tt)**2)
e_sum=np.append(e_sum,e.mean())
# 収束の確認
e_stop=0.01 # 収束時の誤差の大きさ
if e_sum[-1]<e_stop:
print('更新回数= ',(i+1)*(j+1),' で誤差が',e_stop,' 未満となる--->>','平均2乗和誤差=',e_sum[-1])
flg=True
break
if flg:
break
# 学習ループの終端
# 結果の表示
np.set_printoptions(formatter={'float': '{:.3f}'.format, 'int': '{:06d}'.format})
#print(f'e_defw={e_defw.T}\te_defb={e_defb.T}')
print('\n学習結果')
print(f'平均2乗和誤差 = {e_sum[-1]}')
print('誤差の推移\n',e_sum.T)
# グラフの表示(1行に2つのグラフを表示)
spec = gridspec.GridSpec(ncols=2, nrows=1,width_ratios=[1, 2])
fig = plt.figure(dpi=100, figsize=(10,6)) # 横,高さ [インチ]
ax1 = fig.add_subplot(spec[0]) # fig.add_subplot(1,2,1) spec なしの時の位置指定
ax2 = fig.add_subplot(spec[1],projection='3d')
# 平均2乗誤差のグラフ(左のグラフ)
ax1.set_xlabel('更新回数')
ax1.set_ylabel('平均2乗和誤差')
ax1.grid()
idxes = np.arange(e_sum.size)
ax1.plot(idxes,e_sum)
# 学習データと学習結果のグラフ(右のグラフ)
ax2.set_title("学習結果",size=15) # グラフタイトル
# 軸ラベルのサイズと色
ax2.set_xlabel("x1",size=10,color="black")
ax2.set_ylabel("x2",size=10,color="black")
ax2.set_zlabel("出力",size=10,color="black")
ax2.grid()
ax2.view_init(elev=30, azim=150)
# 散布図
ax2.scatter(x1,x2,t,s=3,c="blue",label='Train') # 学習データ
# 学習後の疑似曲面描画のためのデータを作成
seido=100
vx=np.linspace(x1.min(),x1.max(),seido)
vy=np.linspace(x2.min(),x2.max(),seido)
X, Y = np.meshgrid(vx,vy)
Z=np.array([[]])
for xx,yy in zip(X,Y):
for xxx,yyy in zip(xx,yy):
ddd=np.array([[xxx],[yyy]])
Z=np.append(Z,nn.forward(ddd))
X=np.ravel(X)
Y=np.ravel(Y)
ax2.scatter(X,Y,Z,s=1,c='r',label='Test',alpha=0.1) # 学習後
# 凡例の表示
ax2.legend()
plt.show()1エポックあたりのミニバッチ数= 20
学習結果
平均2乗和誤差 = 5.1056085954954415
誤差の推移
[1825.081 244.053 56.880 ... 4.502 1.741 5.106]

線形回帰(特徴量2、出力1、平均2乗誤差を勾配法で学習)での出力は、きれいな1枚の平面(当たり前だが)であるのに対し、ニューラルネットワークでは、ゆがみのある面での結果となった。ニューラルネットワークの出力は、小さな平面での近似解となるのかな?
上の出力は誤差を含めた学習データなので、誤差の無い2数の和となる学習データで学習させたが、1枚の平面とならず同様の出力となった。
10000回の学習後の結果
最終平均2乗和誤差 = 0.17226351478291782
学習範囲のテストデータでは、-0.2~5%弱の誤差
学習範囲外のテストデータでは、数%~15%程度の誤差
誤差の無い学習データでもっと学習をさせたら、1枚の平面出力が得られるのだろうか?実用価値のかけらもないことだが、誤差のない足し算ができるニューラルネットワークができたら、各層の重みがどのような分布になっていて、各重みにどのような働きがあるのか探ってみたい。また、学習範囲外のテストデータの精度について調べてみたい。(以下参考出力。この面が1枚の平面になることを目指す)

線形回帰で曲線、曲面での出力は、特徴量の2乗項、3乗項を追加する必要があったが、ニューラルネットワークでは、与えるデータに応じた回帰結果が得られた。(図3)3本の直線でうまく近似されているように見える。活性化関数による表現力の増大はすばらしい。

学習データの標準化
学習の評価と過学習
分類
2入力、2出力の分類用2層ニューラルネットワーク(あやめ)
構成
中間ノードの活性化関数は ReLU
出力ノードの活性化関数はソフトマックス関数
誤差関数は平均交差エントロピー誤差
データの用意
アヤメデータを利用させてもらう(ありがとうございます)
教師データは分布より、作成
データをファイルとして保存
# アヤメのデータ
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# irisデータセットをirisに格納
iris=load_iris()
# irisデータセットをDataFrameに変換
df=pd.DataFrame(iris.data, columns=iris.feature_names)
# データの抽出
dd=np.array([[]])
dd=np.copy(df.iloc[:,2:4])
# 教師データの作成(分布をみて、設定)
tt=np.zeros(300).reshape(150,2)
tt[0:50,0]=1
tt[50:150,1]=1
# データの確認
plt.plot(dd[:,0],dd[:,1],'o',c='r',ms=3)
plt.show()
data=np.hstack([dd,tt])
#データの保存
dfilename="data01_分類.npz"
np.savez(
dfilename,
Data=data, N=150, # key=save_data
)
#========================
ニューラルネットワークのクラス
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from matplotlib import gridspec
from mpl_toolkits.mplot3d import Axes3D
# ニューラルネットワークのクラス定義(分類)
# NN(入力ノード、隠れ層ノード、出力ノード、学習率)
# w1,b1 1層目(入力と隠れ層の間)
# w2,b2 2層目(隠れ層と出力層の間)
#
# test(input_data) 学習済みの実行メソッド
# learn(input_data,train_t) 学習メソッド
# 引数
# input_data , train_t 2次元のndarray(列ベクトル)で処理
#
# 活性化関数
# 隠れ層 ReLU
# 出力層 ソフトマックス
# 誤差関数
# 平均交差エントロピー誤差
class NN:
def __init__(self,nn_in,nn_hid,nn_out,learn_r):
self.inodes=nn_in
self.hnodes=nn_hid
self.onodes=nn_out
# 重みパラメータ。-0.5 〜 0.5 でランダムに初期化。
self.w1 = np.random.rand(self.hnodes, self.inodes) - 0.5
self.w2 = np.random.rand(self.onodes, self.hnodes) - 0.5
self.b1 = (np.random.rand(self.hnodes) - 0.5).reshape(self.hnodes,-1)
self.b2 = (np.random.rand(self.onodes) - 0.5).reshape(self.onodes,-1)
# 学習率
self.learn_rate=learn_r
# 適用する活性化関数を有効にする
# 活性化関数 ReLU
self.relu=lambda x: np.maximum(0, x)
# 活性化関数の微分
self.relu_dash=lambda x: (np.sign(x) + 1) / 2
# 活性化関数 シグモイド 1 / (1 + np.exp(-x))
# expのoverflow対策を施した実装
# x >=0 のとき sigmoid(x) = 1 / (1 + exp(-x))
# x < 0 のとき sigmoid(x) = exp(x) / (1 + exp(x))
self.sigmoid=lambda x: np.exp(np.minimum(x, 0)) / (1 + np.exp(- np.abs(x)))
# 活性化関数の微分
self.sigmoid_dash=lambda x: self.sigmoid(x)*(1-self.sigmoid(x))
# 活性化関数 ソフトマックス
self.softmax=lambda x: np.exp(x)/np.sum(np.exp(x))
# 活性化関数の微分
self.softmax_dash=lambda x: self.softmax(x)*(1-self.softmax(x))
# 活性化関数 恒等関数 定義する必要がない(回帰の時の出力層)
# self.identity=lambda x: x
# 活性化関数の微分
# self.identity_dash=lambda x: 1
pass
# 勾配の計算 1バッチ分 引数は複数データ
def q_diff(self,X,T):
r,c=self.w1.shape
delta_w1=np.zeros(r*c).reshape(r,c)
r,c=self.b1.shape
delta_b1=np.zeros(r*c).reshape(r,c)
r,c=self.w2.shape
delta_w2=np.zeros(r*c).reshape(r,c)
r,c=self.b2.shape
delta_b2=np.zeros(r*c).reshape(r,c)
for xx,tt in zip(X,T):
# 1件分のデータを入力したときの各ノードでの出力
xx=xx.reshape(-1,1)
tt=tt.reshape(-1,1)
h1_out,out=self.forward(xx,1)
# 出力層の誤差
e_out=out-tt # 平均交差エントロピー誤差を利用
# 平均2乗和誤差のときは、出力層の活性化関数の微分をe_outに適用すること
# 隠れ層の誤差
# dif @ w2(e_out-->行ベクトル)、w2.T@e_out(e_out-->列ベクトル)
h_err = self.relu_dash(self.w1@xx) * (self.w2.T@e_out)
# 勾配の平均(または合計)の総和
n=X[0,:].size
delta_w1+=h_err@xx.T / n
delta_b1+=h_err / n
delta_w2+=(e_out@h1_out.T ) / n
delta_b2+=e_out / n
return delta_w1,delta_b1,delta_w2,delta_b2
# 順方(学習結果の利用)引数は1データ
def forward(self,x,ck=0):
x=x.reshape(-1,1)
h1_out=self.relu(self.w1 @ x + self.b1) # 活性化関数の適用
out=self.softmax(self.w2 @ h1_out + self.b2) # 活性化関数の適用
if ck==0:
return out #self.w2 @ self.activation(self.w1 @ x + self.b1) + self.b2
else:
return h1_out,out
# 逆方向(学習) 引数は複数データ
def backward(self,X, T):
delta_w1,delta_b1,delta_w2,delta_b2=self.q_diff(X,T)
# 重みの更新(学習)
self.w1 -= self.learn_rate * delta_w1
self.b1 -= self.learn_rate * delta_b1
self.w2 -= self.learn_rate * delta_w2
self.b2 -= self.learn_rate * delta_b2
pass
# 問い合わせ
# 順方向(1件分のデータ)
def test(self,input_data): # 中間層出力の返り値なし。学習中はforward(self,x,ck=1)で利用
return self.forward(input_data)
# 逆方向(学習) 入力データは複数データ(バッチサイズのデータ)
def learn(self,input_data,train_t):
return self.backward(input_data,train_t)
# 勾配計算のデバッグ用 (q_diffは学習で利用)
def diff(self,input_data,train_t):
return self.q_diff(input_data,train_t)
pass実行
150件のデータを、学習用100件、テスト用50件にわける
ミニバッチサイズを5件とした確率的勾配降下法とする
# =============================動作確認
# データ読み込み
dfilename="data01_分類.npz"
data=np.load(dfilename)
train_count=data['N']
print(train_count)
d=data['Data']
X=d[:,0:2]
T=d[:,2:4]
# データを学習用とテスト用に分ける
index=np.arange(train_count) # データ数のインデックスを生成
np.random.shuffle(index) # インデックスをシャッフル
split_size=50 #<<<==========テストデータ数
n=list([split_size])
index_split=np.array(np.split(index, n)) # 分割されたインデックスの2次元配列
# 端数が出るときは警告が出る VisibleDeprecationWarning:
test_x=X[index_split[0]]
test_t=T[index_split[0]]
x=X[index_split[1]]
t=T[index_split[1]]
x1=x[:,0]
x2=x[:,1]
print('学習データ 1件 ',x[0],' 件数 ',x.sha pe)
print('テストデータ 1件 ',test_x[0],' 件数 ',test_x.shape)
train_count-=split_size
# 正解率の計算用関数(2分類用 --> n分類用に改良すること)
def seikai(x,t):
ct=cf=0
for xx,tt in zip(x,t):
test=nn.forward(xx).T
if test[0,0]>=0.5:
if tt[0]==1:
ct+=1
else:
cf+=1
else:
if tt[0]==0:
ct+=1
else:
cf+=1
return ct/(ct+cf)*100
# NNの構成
nn_in = 2 # 入力ノード数
nn_out = 2 # 出力ノード数
nn_hidden = 512 # 隠れ層のノード数
learn_rate=0.01 # 学習率
nn=NN(nn_in,nn_hidden,nn_out,learn_rate) # NNのオブジェクト生成
# 学習の設定等
epoch=10 # エポック数
# バッチサイズ
#bach_size=1 # オンライン確率的勾配降下法(SGD)
bach_size=5 # ミニバッチSGDのバッチサイズ
#bach_size=train_count # 勾配降下法(全データ利用)
# バッチサイズのデータに分割
bach_n=(train_count+bach_size-1)//bach_size # 1エポックに必要なバッチ処理回数
index=np.arange(train_count) # 確率的勾配降下のバッチ処理用
print('1エポックあたりのミニバッチ数=',bach_n,' バッチサイズ=',bach_size)
# 誤差等の変数
e_sum=np.array([]) # 学習ごとの平均誤差(学習データ)
e_test=np.array([]) # 学習ごとの平均誤差(テストデータ)
strain=np.array([]) # 学習ごとの正解率(学習データ)
stest=np.array([]) # 学習ごとの正解率(テストデータ)
# 学習の開始
for i in range(epoch):
# 1エポックごとにデータをシャッフルし、ミニバッチデータを作成
np.random.shuffle(index) # インデックスをシャッフル
n=list(range(bach_size,train_count,bach_size)) # 例 [20, 40, 60, 80] 分割する位置の生成
index_split=np.array(np.split(index, n)) # 分割されたインデックスの2次元配列
# bach_n 回で、1エポック分の処理
flg=False # 2重ループを抜けるためのフラグ
for j in range(bach_n):
# 分割されたインデックスに該当するデータ
x_bach=x[index_split[j]]
t_bach=t[index_split[j]]
nn.learn(x_bach,t_bach) # 学習<<<<<------------------------
# 更新ごとの誤差の計算(学習データ)
e=np.array([])
for xx,tt in zip(x,t):
out=nn.forward(xx).T
#e=np.append(e,(out-tt)**2) #平均2乗和誤差
e=np.append(e,-1*(tt@np.log(out.reshape(-1)))) #平均交差エントロピー誤差
e_sum=np.append(e_sum,e.mean())
# 更新ごとの誤差の計算(テストデータ)
et=np.array([])
for xx,tt in zip(test_x,test_t):
out=nn.forward(xx).T
#et=np.append(et,(nn.forward(xx).T-tt)**2) #平均2乗和誤差
et=np.append(e,-1*(tt@np.log(out.reshape(-1)))) #平均交差エントロピー誤差
e_test=np.append(e_test,et.mean())
# 正解率の計算
strain=np.append(strain,seikai(x,t)) # 学習データ
stest=np.append(stest,seikai(test_x,test_t)) # テストデータ
# 収束の確認
e_stop=0.001 # 収束時の誤差の大きさ
if e_sum[-1]<e_stop:
print('更新回数= ',(i+1)*(j+1),' で誤差が',e_stop,' 未満となる--->>','平均交差エントロピー誤差=',e_sum[-1])
flg=True
break
if flg:
break
# 学習ループの終端
# 結果の表示
np.set_printoptions(formatter={'float': '{:.3f}'.format, 'int': '{:06d}'.format})
#print(f'e_defw={e_defw.T}\te_defb={e_defb.T}')
print('\n学習結果')
print(f'平均交差エントロピー誤差 = {e_sum[-11:-1]}')
#print('誤差の推移\n',e_sum.T)
print("\n学 習データでの正解率 = ",seikai(x,t))
print("テストデータでの正解率 = ",seikai(test_x,test_t))
#print(strain[-11:-1])
#print(stest[-11:-1])実行結果(中間層ノード数 512)
150
学習データ 1件 [3.800 1.100] 件数 (100, 2)
テストデータ 1件 [4.800 1.800] 件数 (50, 2)
1エポックあたりのミニバッチ数= 20 バッチサイズ= 5
学習結果
平均交差エントロピー誤差 = [0.020 0.020 0.021 0.021 0.021 0.020 0.020 0.020 0.020 0.020]
学 習データでの正解率 = 100.0
テストデータでの正解率 = 100.0
グラフの作成(可視化)
# グラフの表示(1行に3つのグラフを表示)
spec = gridspec.GridSpec(ncols=3, nrows=1,width_ratios=[1,1,2])
fig = plt.figure(dpi=100, figsize=(10,6)) # 横,高さ [インチ]
ax1 = fig.add_subplot(spec[0]) # fig.add_subplot(1,2,1) spec なしの時の位置指定
ax2 = fig.add_subplot(spec[1])
ax3 = fig.add_subplot(spec[2],projection='3d')
# 平均2乗誤差のグラフ(左のグラフ)
idxes = np.arange(e_sum.size)
ax1.set_xlabel('更新回数')
ax1.set_ylabel('平均交差エントロピー誤差')
ax1.grid()
ax1.plot(idxes,e_sum,label='Train')
ax1.plot(idxes,e_test,label='test')
ax2.set_xlabel('更新回数')
ax2.set_ylabel('正解率')
ax2.grid()
ax2.plot(idxes,strain,label='Train')
ax2.plot(idxes,stest,label='test')
# 学習データの散布図
ax3.set_xlabel('x1')
ax3.set_ylabel('x2')
ax3.grid()
ax3.view_init(azim=80,elev=75 ) # 115 70 115 35 110 85
ttt=t[:,0]
ax3.scatter(x1[ttt==1],x2[ttt==1],ttt[ttt==1],s=2,c="blue",label='Train1')
ax3.scatter(x1[ttt==0],x2[ttt==0],ttt[ttt==0],s=2,c="slateblue",label='Train0')
ttt=test_t[:,0]
ax3.scatter(test_x[:,0][ttt==1],test_x[:,1][ttt==1],ttt[ttt==1],s=2,c="red",label='Test1')
ax3.scatter(test_x[:,0][ttt==0],test_x[:,1][ttt==0],ttt[ttt==0],s=2,c="deeppink",label='Test0')
# 学習後の疑似曲面描画のためのデータを作成
seido=100
haba=1
x_min=x1.min()-haba
x_max=x1.max()+haba
y_min=x2.min()-haba
y_max=x2.max()+haba
vx=np.linspace(x_min,x_max,seido)
vy=np.linspace(y_min,y_max,seido)
X, Y = np.meshgrid(vx,vy)
Z=np.array([[]])
for xx,yy in zip(X,Y):
for xxx,yyy in zip(xx,yy):
ddd=np.array([[xxx],[yyy]])
Z=np.append(Z,nn.forward(ddd)[0,0])
X=np.ravel(X)
Y=np.ravel(Y)
ax3.scatter(X,Y,Z>=0.5,s=1,c='r',label='Test分類',alpha=0.1) # 学習後(0.5以上で1)Z>=0.5 --> 1 OR 0
ax3.scatter(X,Y,Z,s=1,c='m',label='Test出力',alpha=0.1) # 学習後
# 凡例の表示
ax1.legend()
ax2.legend()
ax3.legend()
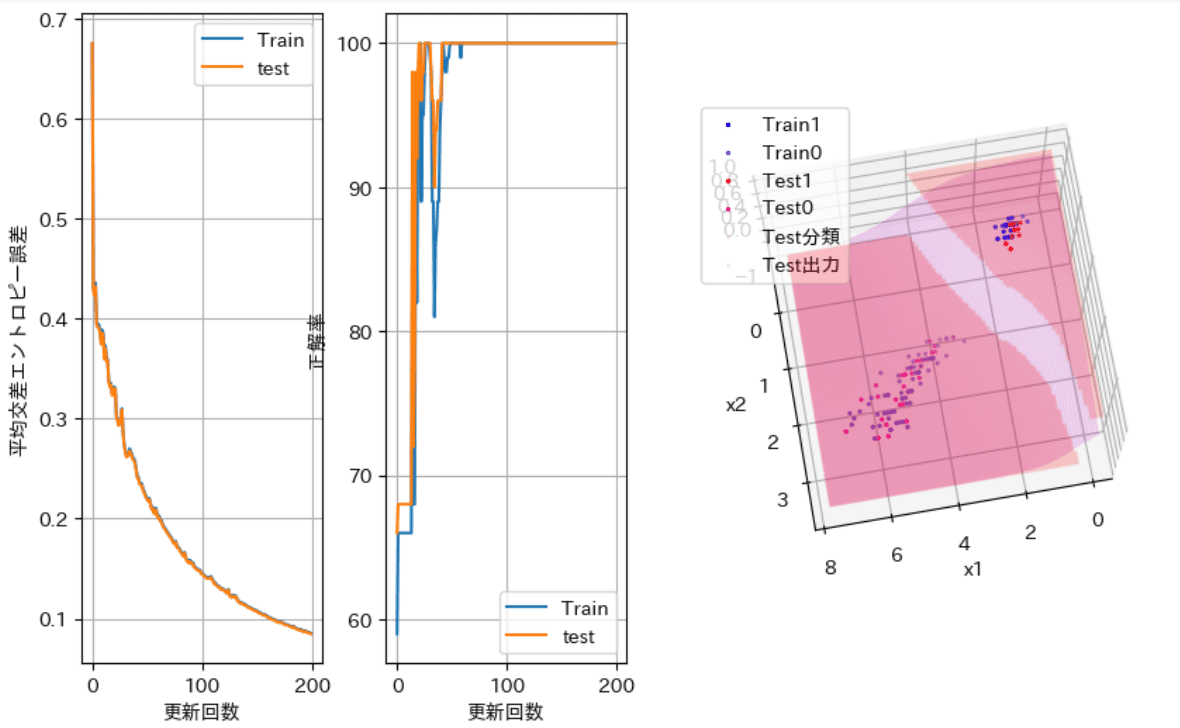
plt.show()中間層のノード数の違いでの出力例
誤差は、更新回数が20~30回のあたりで若干停滞ぎみに振動しながら収束へ向かっている。ノード数が大きいほど速く収束し、「振動しながらの部分」が早い段階で起こっている。
正解率は、先の振動する部分を経て100%に達している。(容易に分類できるデータすぎたかな?)
学習データ、テストデータとも同様の変化をしている。


64入力、10出力の分類用2層ニューラルネットワーク(手書き数字)
MNIST手書き数字のデータを使わせていただきました。ありがとうございます。
データ数 1797 件
1つのデータ 8×8の画像情報(1区画の値:0~16)
ニューラルネットワークの構成
入力 64ノード 中間層 1024ノード 出力 10ノード
# データの作成
from sklearn import datasets
####MNIST手書き数字のデータ読み込み####
digits = datasets.load_digits()
digits.data[1] #1次元データに変換された8*8の画像データ
digits.target # 教師データ
n,m=digits.data.shape
# 教師データ(0~9)を出力ノード10に振り分けて、該当要素を1にする
train_t1=digits.target.reshape(-1,1)
train_t=np.zeros(n*10).reshape(-1,10)
for i in range(10):
train_t[:,i].reshape(-1,1)[train_t1==i]=1
dfilename="data202_分類手書き数字.npz"
np.savez(
dfilename,
Data=digits.data, T=train_t, N=n, # key=save_data
)# =============================動作確認
# データ読み込み
dfilename="data202_分類手書き数字.npz"
data=np.load(dfilename)
train_count=data['N']
print(train_count)
X=data['Data']
T=data['T']
# データを学習用とテスト用に分ける
index=np.arange(train_count) # データ数のインデックスを生成
np.random.shuffle(index) # インデックスをシャッフル
split_size=200 #<<<==========テストデータ数
n=list([split_size])
index_split=np.array(np.split(index, n)) # 分割されたインデックスの2次元配列
# 端数が出るときは警告が出る VisibleDeprecationWarning:
test_x=X[index_split[0]]
test_t=T[index_split[0]]
x=X[index_split[1]]
t=T[index_split[1]]
x1=x[:,0]
x2=x[:,1]
print(' 学 習データ件数 ',x.shape) #'学 習データ 1件 ',x[0],
print(' テストデータ件数 ',test_x.shape) #'テストデータ 1件 ',test_x[0],
train_count-=split_size
# 正解率の計算用関数
# tt 要素番号 0~9 --> 手書き数字の値 0~9 ttの要素が 1:該当数字 (それ以外は0)
def seikai(x,t):
ct=cf=0
for xx,tt in zip(x,t):
test=nn.forward(xx).T
u, indices = np.unique(tt, return_index=True) #u:ttのユニークな値(昇順)indices:uの最初の要素番号
ind_tt=indices[-1]
u, indices = np.unique(test, return_index=True)
ind_test=indices[-1]
if ind_test==ind_tt and u[-1]>0.1: #testとttの最大値の要素番号が一致 and 要素が0.1を超える
ct+=1
else:
cf+=1
return ct/(ct+cf)*100
# NNの構成
nn_in = 64 # 入力ノード数
nn_out = 10 # 出力ノード数
nn_hidden = 1024 # 隠れ層のノード数
learn_rate=0.01 # 学習率
nn=NN(nn_in,nn_hidden,nn_out,learn_rate) # NNのオブジェクト生成
# 学習の設定等
epoch=5 # エポック数 10 バッチ5 で23分かかった
# バッチサイズ
#bach_size=1 # オンライン確率的勾配降下法(SGD)
bach_size=10 # ミニバッチSGDのバッチサイズ
#bach_size=train_count # 勾配降下法(全データ利用)
# バッチサイズのデータに分割
bach_n=(train_count+bach_size-1)//bach_size # 1エポックに必要なバッチ処理回数
index=np.arange(train_count) # 確率的勾配降下のバッチ処理用
print('1エポックあたりのミニバッチ数=',bach_n,' バッチサイズ=',bach_size)
# 誤差等の変数
e_sum=np.array([]) # 学習ごとの平均誤差(学習データ)
e_test=np.array([]) # 学習ごとの平均誤差(テストデータ)
strain=np.array([]) # 学習ごとの正解率(学習データ)
stest=np.array([]) # 学習ごとの正解率(テストデータ)
# 学習の開始
for i in range(epoch):
# 1エポックごとにデータをシャッフルし、ミニバッチデータを作成
np.random.shuffle(index) # インデックスをシャッフル
n=list(range(bach_size,train_count,bach_size)) # 例 [20, 40, 60, 80] 分割する位置の生成
index_split=np.array(np.split(index, n)) # 分割されたインデックスの2次元配列
# bach_n 回で、1エポック分の処理
flg=False # 2重ループを抜けるためのフラグ
for j in range(bach_n):
# 分割されたインデックスに該当するデータ
x_bach=x[index_split[j]]
t_bach=t[index_split[j]]
nn.learn(x_bach,t_bach) # 学習<<<<<------------------------
# 更新ごとの誤差の計算(学習データ)
e=np.array([])
for xx,tt in zip(x,t):
out=nn.forward(xx).T
#e=np.append(e,(out-tt)**2) #平均2乗和誤差
e=np.append(e,-1*(tt@np.log(out.reshape(-1)))) #平均交差エントロピー誤差
e_sum=np.append(e_sum,e.mean())
# 更新ごとの誤差の計算(テストデータ)
et=np.array([])
for xx,tt in zip(test_x,test_t):
out=nn.forward(xx).T
#et=np.append(et,(nn.forward(xx).T-tt)**2) #平均2乗和誤差
et=np.append(e,-1*(tt@np.log(out.reshape(-1)))) #平均交差エントロピー誤差
e_test=np.append(e_test,et.mean())
# 収束の確認
e_stop=0.001 # 収束時の誤差の大きさ
if e_sum[-1]<e_stop:
print('更新回数= ',(i+1)*(j+1),' で誤差が',e_stop,' 未満となる--->>','平均交差エントロピー誤差=',e_sum[-1])
flg=True
break
# 正解率の計算
strain=np.append(strain,seikai(x,t)) # 学習データ
stest=np.append(stest,seikai(test_x,test_t)) # テストデータ
if flg:
break
# 学習ループの終端
# 結果の表示
np.set_printoptions(formatter={'float': '{:.3f}'.format, 'int': '{:06d}'.format})
#print(f'e_defw={e_defw.T}\te_defb={e_defb.T}')
print('\n学習結果')
print(f'平均交差エントロピー誤差 = {e_sum[-11:-1]}')
#print('誤差の推移\n',e_sum.T)
print("\n学 習データでの正解率 = ",seikai(x,t))
print("テストデータでの正解率 = ",seikai(test_x,test_t))
#print(strain[-11:-1])
#print(stest[-11:-1])# グラフの表示(1行に2つのグラフを表示)
spec = gridspec.GridSpec(ncols=2, nrows=1,width_ratios=[1,1])
fig = plt.figure(dpi=100, figsize=(10,6)) # 横,高さ [インチ]
ax1 = fig.add_subplot(spec[0]) # fig.add_subplot(1,2,1) spec なしの時の位置指定
ax2 = fig.add_subplot(spec[1])
#ax3 = fig.add_subplot(spec[2],projection='3d')
# 平均2乗誤差のグラフ(左のグラフ)
idxes = np.arange(e_sum.size)
ax1.set_xlabel('更新回数')
ax1.set_ylabel('平均交差エントロピー誤差')
ax1.grid()
ax1.plot(idxes,e_sum,label='Train')
ax1.plot(idxes,e_test,label='test')
idxes = np.arange(strain.size)+1
ax2.set_xlabel('エポック数')
ax2.set_ylabel('正解率')
ax2.grid()
ax2.plot(idxes,strain,label='Train')
ax2.plot(idxes,stest,label='test')
# 凡例の表示
ax1.legend()
ax2.legend()
plt.show()実行結果(実行時間 2分51秒)
1797
学 習データ 件数 (1597, 64)
テストデータ 件数 (200, 64)
1エポックあたりのミニバッチ数= 160 バッチサイズ= 10
学習結果
平均交差エントロピー誤差 = [0.976 1.136 1.136 1.232 1.232 0.954 0.954 0.951 0.917 1.470]
学 習データでの正解率 = 96.18033813400125
テストデータでの正解率 = 93.5

間違ったテストデータ 13件
(「教師データ」を「FNN出力」に間違えた)
5を7、8を9、9を3、3を7、2を7、3を9、8を2、
9を1、5を6、8を1、1を4、3を8、1を6
人が間違えそうな数字の組み合わせもあるが、NNにとって1はむつかしいのかな?元画像のデータを視覚化して確認してみよう。
誤ったデータの例(エポック数10)
学習結果 平均交差エントロピー誤差 = [0.454 0.454 0.735 0.735 2.496 2.496 2.496 1.806 1.799 1.042]
学 習データでの正解率 = 94.55228553537883
テストデータでの正解率 = 90.5

誤りのデータ(一部 全部で19件)
[0.000 0.000 0.000 0.000 1.000 0.000 0.000 0.000 0.000 0.000]
学習= 4.0 教師= 5.0
[0.000 0.000 0.000 0.000 0.000 0.000 1.000 0.000 0.000 0.000]
学習= 6.0 教師= 4.0
・
・
・
[0.000 0.112 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.888]
学習= 9.0 教師= 1.0
[0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000]
学習= 9.0 教師= 8.0
[0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000]
学習= 9.0 教師= 3.0

# 誤ったデータの表示
test_o=np.array([]) # 学習出力
test_of=np.array([]) # 誤ったときの出力
test_ofd=np.array([]) # 誤ったときの十進数表示
t_ofd=np.array([]) # 教師 十進数表示
d_of=np.array([]) # 誤ったときの元データ
# 正解率の計算用関数(動作確認にあり。確認用の処理を付加したもの)
def seikai(x,t):
ct=cf=0
global test_o,test_of,t_ofd,d_of,test_ofd
for xx,tt in zip(x,t):
test=nn.forward(xx).T
test_o=np.append(test_o,test) #FF出力
u, indices = np.unique(tt, return_index=True)
ind_tt=indices[-1] #教師データ 0~9
u, indices = np.unique(test, return_index=True)
ind_test=indices[-1] #学習データ 0~9
if ind_test==ind_tt: # 誤りを検出
ct+=1
else:
cf+=1
test_of=np.append(test_of,test)
t_ofd=np.append(t_ofd,ind_tt)
test_ofd=np.append(test_ofd,ind_test)
d_of=np.append(d_of,xx)
return ct/(ct+cf)*100
print(seikai(test_x,test_t)) # 正解率の計算
d_of=d_of.reshape(-1,64) # 画像データを分離
test_of=test_of.reshape(-1,10)
m,n=test_of.shape
for i in range(m):
print(test_of[i],' 学習=',test_ofd[i],' 教師=',t_ofd[i])
####誤った数字データの画像表示####
#描画領域の確保
fig, axes = plt.subplots(5, 5, figsize=(15, 15), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.5, wspace=0.5))
#確保した描画領域に誤った画像を表示
for i, ax in enumerate(axes.flat):
ax.imshow(d_of[i].reshape(8,8), cmap=plt.cm.gray_r, interpolation='nearest')
axt=str(int(t_ofd[i]))+'を'+str(int(test_ofd[i]))+'と誤る'
ax.set_title(axt)
エポック30での記録(67分27.7秒)
1エポックあたりのミニバッチ数= 160 バッチサイズ= 10
学習結果
平均交差エントロピー誤差 = [0.003 0.003 0.003 0.012 0.012 0.012 0.012 0.012 0.012 0.012]
学 習データでの正解率 = 99.81214777708203
テストデータでの正解率 = 95.0
95.0
[0.000 0.120 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.880]
学習= 9.0 教師= 1.0
[0.000 0.000 1.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000]
学習= 2.0 教師= 0.0
[0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000]
学習= 9.0 教師= 5.0
[0.000 0.000 0.000 1.000 0.000 0.000 0.000 0.000 0.000 0.000]
学習= 3.0 教師= 7.0
[0.000 0.051 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.949]
学習= 9.0 教師= 1.0
[0.000 1.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000]
学習= 1.0 教師= 8.0
[0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000]
学習= 9.0 教師= 1.0
[0.000 0.000 0.000 0.544 0.000 0.000 0.000 0.000 0.000 0.456]
学習= 3.0 教師= 9.0
[0.000 0.000 0.000 0.000 1.000 0.000 0.000 0.000 0.000 0.000]
学習= 4.0 教師= 5.0
[0.000 0.000 0.000 0.040 0.000 0.000 0.000 0.000 0.960 0.000]
学習= 8.0 教師= 3.0

8個目の「9を3に誤った」部分は、0.456(9)と0.544(3)で僅差で9と出力されている。画像の上、中、下のうちの上の入力につながるノードに関係するFNNの重みの中に、9と3の分類を決める強い因子があるのかもと・・・(調べてないので、なんとなくそう思う)
1と9の分類が難しいようである。画像をみると仕方ないかな。手書きデータの前処理で、数字の特徴をうまく引き出す工夫がいるようだ。重みの状態を確認したいが、今のFNNクラスでは無理なので、各パラメータを出力できるように変更しよう。

もっと学習させたら、学習データでの正解率が100%に収束するのだろうか。テストデータでの正解率は、95%あたりに収束しているようにみえる。(このあたりが限界かもしれない?)
学習データでの正解率が100%になっても、テストデータでの正解率がこれ以上高くならないとしたら、その原因はどこにあるのだろうか。
図8、9、12の正解率は1回きりの分割データでの出力である。分割交差検証するには、PCの力不足が否めない。どうしようかな。
データを変更して、確かめてみよう。また、自分で手書きデータを作成して分類させてみよう。
雑感
FNNの基本的な動作については、少し理解できたかな。画像認識では、畳み込み層、プーリング層などを追加した多層NNを構成するといいようだ。さらに、教師なし学習の仕組みも理解したいな。これらは、新しいページに記録します。
単なる数値計算に過ぎないのに、興味深い結果を出力できるアルゴリズムがいっぱいあることに驚かされます。
量子の世界では波動関数はすごい式ですが、行列で表現している式を以前どこかでみたような記憶が。ニューラルネットワークでの行列(単なる数値の集まり)がこんなにすごい表現力をもっていることにびっくり。便利な計算ツール程度にしか思っていなかったことに少し後悔。
あとがき
自分の覚書として記録したものなので、表現のまずさ、内容の誤りが多々あるページだと思います。にもかかわらず「すき」をマークしていただいた方に感謝しています。
何かの偶然でこのページに出会ってしまって閲覧された方は、目的を果たせなかったことと思います。ごめんなさい。それでも、なにか役立つことがあったとしたら幸いです。
この記事が気に入ったらサポートをしてみませんか?
