F90Answer　ｐ295　test2

解決に一歩前進したので、レポート
↓は前回の記事、エラー解決できずに沼ってた

参考書は、「Fortran90/95　アンサーブック」

ｐ296よく見たら、”演習6.16と同じサブルーチンを使用”ってコメントアウトしてあるの気付かずにコーディングしてた・・・

↓はコンパイル成功したときのコード

module subprogs
    implicit none
    real(8), parameter:: pi = acos(-1.0d0) ! 共有変数
contains
    subroutine explicit_diff2d(phi, phi2, x, n1, n2, nstep, &
        d1, d2, ero, fo1d, fo2d, pstep)
    ! オイラー陽解法と中央差分で離散化した2次元拡散方程式を計算
    integer, intent(in) :: n1, n2, nstep, fo1d, fo2d, pstep
    real(8), intent(inout) :: phi(n1, n2), phi2(n1, n2)
    real(8), intent(in) :: x(2, n1, n2)
    real(8), intent(in) :: d1, d2, ero
    integer istep, i, j
    real (8) er
        do istep = 1, nstep ! nstep まで時間進行の反復演算を行う
            do j = 2, n2-1 ! 境界を除く内部のphi の値を計算
                do i = 2, n1-1
                    phi2(i, j) = phi(i, j) &
                        +d1 * (phi(i-1, j) - 2.0d0 * phi(i, j) &
                            + phi(i+1, j)) &
                        + d2 * (phi(i, j-1) - 2.0d0 * phi(i, j) &
                            + phi(i, j+1))
                enddo
            enddo
            er = chk_steady(phi, phi2, n1, n2) !定常性のチェック
            if (mod(istep, pstep) == 0) then ! pstep ごとに出力
                write(*, *) 'istep, er = ', istep, er
                call output_results(phi, x, n1, n2, fo1d, fo2d)
            endif
            if (er < ero) exit ! 定常解となっていれば終了
                phi(:, :) = phi2(:, :) ! 結果の更新
        enddo
        write(*, *) 'istep, er = ', &
            istep, chk_steady(phi, phi2, n1, n2)
    end subroutine explicit_diff2d
    
    function chk_steady(phi, phi2, n1, n2) result(er)
        ! 時間ステップ間のphi の差の2乗和を返す関数
        integer, intent(in) :: n1, n2
        real(8), intent(in) :: phi(n1, n2), phi2(n1, n2)
        real(8) er
        integer i, j
        er =0.0d0
        do j = 1, n2
            do i = 1, n1
                er = er + (phi(i, j) -  phi2(i, j)) ** 2
            enddo
        enddo
        er = sqrt(er)
    end function chk_steady
    
    subroutine set_dbc(p, x, n1, n2)
    !...(演習 6.16のモジュールサブルーチンと同じ)...
        ! [境界条件D] の設定
        integer, intent(in) :: n1, n2
        real(8), intent(out) :: p(n1,n2)
        real(8), intent(in) :: x(2, n1, n2)
        p(1, 1:n2) = 0.0d0
        p(n1, 1:n2) = 0.0d0
        p(1:n1, n2) = 0.0d0
        p(1:n1, 1) = sin(pi * x(1, 1:n1, 1))
    end subroutine set_dbc
    
    subroutine output_results(phi, x, n1, n2, fo1d, fo2d)
    !...(演習 6.16のモジュールサブルーチンと同じ)...
        ! 計算結果のファイル出力
        integer, intent(in) :: n1, n2, fo1d, fo2d
        real (8), intent(in) :: phi(n1, n2), x(2, n1, n2)
        integer i, j, ic, jc
        ! x1, x2 中央線上の phi と理論解のファイル出力
        ic = (1 + n1) / 2
        jc = (1 + n2) / 2
        do j = 1, n2
            write(fo1d, *) x(2, ic, j), phi(ic, j), &
                theory(x, ic, j, n1, n2)
        enddo
        write(fo1d, *) ''
        do i = 1, n1
            write(fo1d, *) x(1, i, jc), phi(i, jc), &
                theory(x, i, jc, n1, n2)
        enddo
        write(fo1d, *) ''
        ! x1, x2 座標 phi のファイル出力
        do j = 1, n2
            do i = 1, n1
                write(fo2d, '(4e12.4)') x(:, 1, j), phi(i, j)
            enddo
            write(fo2d, *) ''
        enddo
        write(fo2d, *) ''
    end subroutine output_results
    
    function theory(x, i, j, n1, n2) result(th)
    !...(演習 6.16のモジュール関数と同じ)...
        ! [境界条件D]の定常解の理解を返す関数
        integer, intent(in) :: n1, n2, i, j
        real(8), intent(in) :: x(2, n1, n2)
        real (8) th
        th = sin(pi * x(1, i, j)) &
            * sinh(pi * (1.0d0 - x(2, i, j))) / sinh(pi)
    end function theory
    
    subroutine set_x(x, dx, n1, n2)
    !...(演習 6.16のモジュールサブルーチンと同じ)...
        ! 格子点座標の設定
        integer, intent(in) :: n1, n2
        real(8), intent(out) :: x(2, n1, n2), dx(2)
        integer i, j
        dx(1) = 1.0d0 / dble(n1 - 1)
        dx(2) = 1.0d0 / dble(n2 - 1)
        do j = 1, n2
            do i = 1, n1
                x(1, i, j) = dx(1) * dble(i - 1)
                x(2, 1, j) = dx(2) * dble(j - 1)
            enddo
        enddo
    end subroutine set_x
end module subprogs
    
program main
    use subprogs
    implicit none
    integer, parameter :: n1 = 51 , n2 = 51
    integer :: fo1d = 20 , fo2d = 30, nstep = 10 ** 4, pstep = 1000
    real(8) :: dt = 1.0d-4, alp = 5.0d-1, er0 = 1.0d-6
    real(8) d1, d2
    real (8) phi (n1, n2), phi2(n1, n2), x(2, n1, n2), dx(2)
    call set_x(x, dx, n1, n2)
    ! 拡散数d1, d2 を求めて出力
    d1 = alp * dt / (dx(1) ** 2)
    d2 = alp * dt / (dx(2) ** 2)
    write(*, *) 'd1, d2 = ', d1, d2
    write(*, *) 'd1 + d2 (< 0.5) = ', d1 + d2
    ! 出力ファイルをopen
    open (fo1d, file = 'diffusion1d.txt')
    open (fo2d, file = 'diffusion2d.txt')
    ! 初期・境界条件の設定
    phi(2:n1-1, 2:n2-1) = 0.0d0 ! 初期条件の設定
    call set_dbc(phi, x, n1, n2) ! ディリクレ境界条件の設定
    call set_dbc(phi2, x, n1, n2) ! ディリクレ境界条件の設定
    ! 拡散方程式の非定常計算 
    call explicit_diff2d(phi, phi2, x, n1, n2, nstep, &    
        d1, d2, er0, fo1d, fo2d, pstep)
    ! 最終結果の出力と出力ファイルをclose
    call output_results (phi, x, n1, n2, fo1d, fo2d)
    close(fo1d)
    close(fo2d)
    write(*, *) 'normal end, check output files...'
end program main

追記して、コンパイルするたびに出るエラー治して、何とか描画できた。
※多かったエラー（　l　⇒　1　、　1　⇒　i　、　o　⇒　0）

↓はコンパイル画面

PS C:\fortran> gfortran -g -o f90_answer_295_vs f90_answer_295_vs.f90
PS C:\fortran> ./f90_answer_295_vs.exe
 d1, d2 =   0.12500000000000000       0.12500000000000000     
 d1 + d2 (< 0.5) =   0.25000000000000000
 istep, er =         1000   3.2207609648897033E-003
 istep, er =         2000   1.0968355134492991E-003
 istep, er =         3000   4.0667464434826533E-004
 istep, er =         4000   1.5150641624050719E-004
 istep, er =         5000   5.6457692083098355E-005
 istep, er =         6000   2.1038792798289827E-005
 istep, er =         7000   7.8400494516255078E-006
 istep, er =         8000   2.9215734056939310E-006
 istep, er =         9000   1.0887164976506565E-006
 istep, er =         9087   9.9912017826445112E-007
 normal end, check output files...

↓は、powershellでのコード、と、gnuplotで出力したグラフ

gnuplot> plot 'C:/fortran/diffusion1d.txt' with lines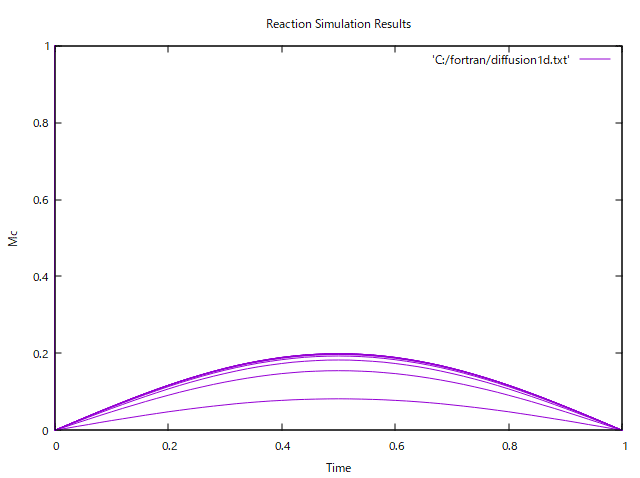

とりあえず沼脱出
もう少し深堀っていきたい