E資格【ラビット チャレンジ】機械学習 1/2
【学習ポイント】 ※本単元の学習の狙い
①機械学習の基本的な手法を理解し実装する
②機械学習モデリングの流れを理解
・特にモデルの数学的に背景を理解しつつ、それをコンピュータへ
Phthonプログラムとして実装・実行するために、どのように行われ
て計算量の低減させているか確認・理解する。
序章
[1] 要点のまとめ
① 機械学習モデリングプロセス

②スコープ(本講義で扱う内容)

③機械学習モデル

トム・M・ミッチェルによる定義
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience 。
コンピュータプログラムがタスクのクラスTと性能指標Pに関し経験Eから学習するとは、T内のタスクのPで測った性能が経験Eにより改善される事を言う。
タスク : プログラムが解くべき課題
経験 : なんらかのデータとしてプログラムに与えられる。
学習 : 経験からプログラムの性能を改善する過程
性能指標 : プログラムがタスクをどの程度の性能で達成したかを測る
出典: ウィキペディア
→ 自分なりに説明できるようになることが大切
→ 機械学習は、個々のタスク解決に向けて、数学ベースに
コンピューターへ学習の仕方を人がプログラムとして
命令・実行して自律的な性能指標の改善を目指すこと。
第1章 線形回帰モデル
アウトライン
→ 線形は比例関係をベースにしている
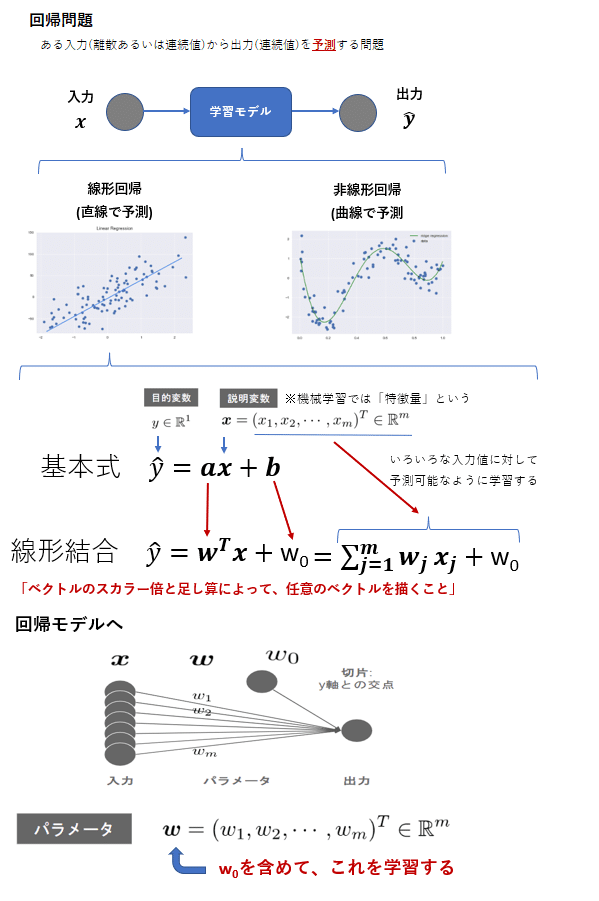
線形回帰モデル

線形回帰モデルと数式モデルの関係
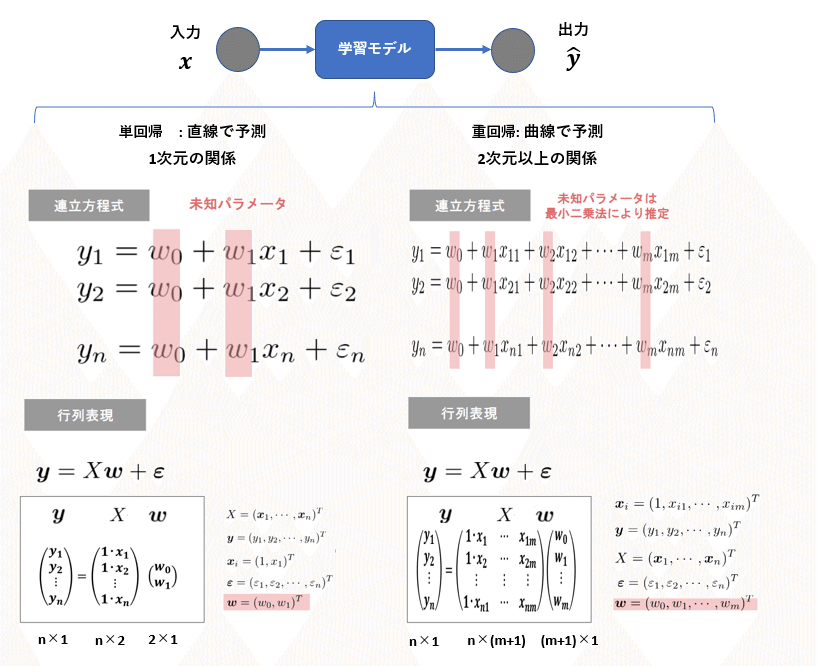
パラメータの推定とモデルの評価

→ 機械学習モデルでは、パラメータ推定を元データを分割して学習に
利用するデータである「学習用データ」と、学習済みモデルの精度を
検証するためのデータである検証用データの2つを使う。
→ 分割は機械学習モデルの汎化性能(Generalization)を測定するため、
データへの当てはまりの良さではなく、未知のデータに対して
どれくらい精度が高いかを測ることが目的である。
数式の展開






[2] 実装演習結果キャプチャー又はサマリーと考察
① np_regression.ipynb
numpyベースの実装を体感するため、単回析分析について数式と対応付けながらnp_regression.ipynbを動作確認を行った。重回帰分析も内容確認したが
講義で習った数式から一捻りされており、数学の数式からPythonのプログラムへ展開する基本スキルの向上の必要性を感じた。
また確認に際してはcov関数の引数について調べると共に、英略号されている変数名ついて、敢えてフルスペルと日本語の意味を確認した。
Pythonは基礎的なことしか習得していないので、他者が書いたプログラムをリバースエンジニアリングライクに地道に分析を繰り返しを重ねて馴れるしかないと思われる。

②skl_regression.ipynb
sklearnベースの実装を体感するため、講義動画と同様に
線形回帰モデル-Boston Hausing Data-
の動作確認を行ってライブラリーの有難みも少しは体感した。
講義動画と同様に部屋を変数とした感度分析ライクに変化させた
プライスの予測結果を単回帰と重回帰で一覧表と散布図を作成
してみた。
今回は非常に単純な特徴量の選択しか行っていないが、実務上
では当該領域のドメイン知識を背景に統計学的なアプローチでの
モデルや結果の評価も必要と感じた。


[3] 加点レポート
今回も黒本の線形回帰の問題・解説の確認を行った。
第7章 教師あり学習の各種アルゴリズム

第2章 非線形回帰モデル
[1] 要点のまとめ
アウトライン
複雑な非線形構造を内在する現象に対して、非線形回帰モデリングを
適用する
<ポイント>
・データの構造を線形で捉えられる場合は限られる
・非線形な構造を捉えられる仕組みが必要非線形回帰モデル

非線形の数学的な予測モデルは以下のとおりとなる。

基底展開法
<ポイント>
・回帰関数として、基底関数と呼ばれる既知の非線形関数と
パラメータベクトルの線型結合を使用
・学習によって求めるべき未知パラメータは、線形回帰モデルと
同様に最小2乗法や最尤法により推定
一次元の基底関数に基づく非線形回帰

よく使われる基底関数には、上記のような多項式関数、ガウス型基底関数の他にスプライン関数/ Bスプライン関数がある。
スプライン関数は、数多くの回帰係数によって表されるにもかかわらず、得られる曲線は滑らかなもので、 回帰係数の数を少なくすることを意図しないノンパラメトリック回帰として用いられることが多い。B-スプラインを利用すると、数値計算の分量は多くなるけれどもアルゴリズムは容易になる。
基底関数の数式展開について


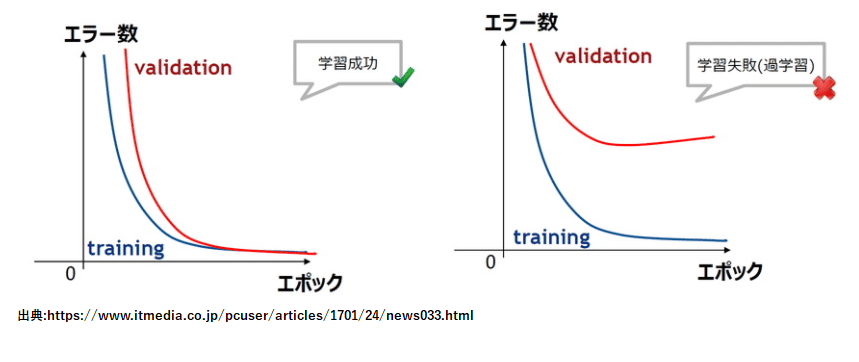
未学習(underfitting)と過学習(overfitting)について


正則化法について
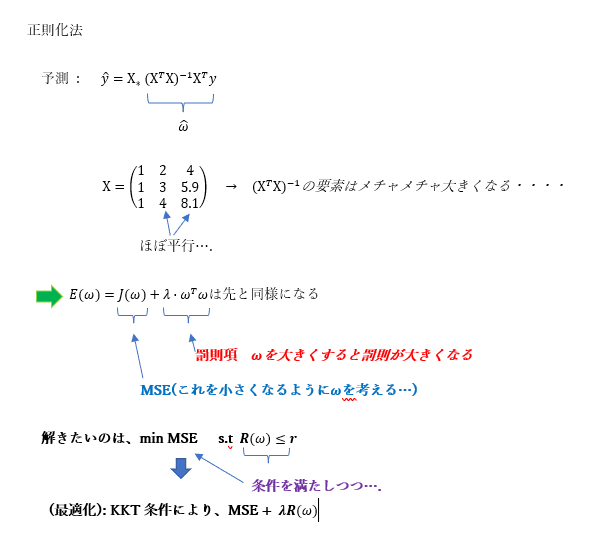
正則化項の役割

パラメータの推定とモデルの評価
基本的なアプローチは線形回帰と同様。
過学習の事例
ホールドアウト法とクロスバリデーション(交差検証)

グリッドサーチ ( Grid Search )
機械学習においてモデルの精度を向上させるための手法のことで、
設定した全てのハイパーパラメータの組み合わせを試し、その中で
最も良いスコアを得たモデルを探す方法

[2] 実装演習結果キャプチャー又はサマリーと考察
"skl_nonlinear regression.ipynb"を使って実装演習を行った。
① KernelRidgeにおいて、kernelを次の通り変更して
学習結果を決定係数とグラフで確認した。
kernel_names= ['rbf','poly','sigmoid','linear']

② #Ridge rbf_kernelにおいて、gammaを次の通り変更して
学習結果を決定係数とグラフで確認した。
gamma= [10,50,100,300]
gamma=300とすると過学習の傾向がみられる。

[3] 加点レポート
今回も黒本の線形回帰の問題・解説の確認を行った。
第6章 モデルの評価・正則化・ハイパーパラメータ探索
1. あるデータ集合を用いて教師あり学習を行う場合、一般に、このデータ
集合から訓練集合、検証集合、テスト集合の3種類の集合を作り、
これ ら集合を用いてモデルの学習や評価を行う。
これら3つの集合を用いた モデルの評価方法として、
・ データ集合を7:3の割合で分割し、7割のほうを訓練集合、
3割のほうをテスト集合にした。得られた訓練集合を用いて
訓練し、テスト集合を用いて汎化誤差を推定した。
・データ集合内のデータ数が10000件もあったため、データ集合を
9:1の割合で分割し、9割のほうを訓練集合、1割のほうをテスト
集合にした。得られた訓練集合を用いて訓練し、テスト集合を
用いて汎化誤差を推定した。
・データ集合を7:3に分割し、3割のほうをテスト集合にした。
残りの7割のほうをさらに8:2に分割し、8割のほうを訓練集合、
2割 のほうを検証集合にした。得られた訓練集合を用いて訓練を
行い、テスト集合を用いて汎化誤差を推定した。検証集合は、
ハ イパーパラメータを決定するために使用した。
などがある。
2. 学習済みのモデルを評価する方法として、ホールドアウト法とk-分割
交差検証法がある。これらの評価方法に関する記述として、
・ホールドアウト法・k-分割交差検証法のいずれも、検証集合
またはテスト集合に対する予測結果を用いてモデルの汎化性能を
評価する。
・ ホールドアウト法で汎化性能を評価する場合は、データ集合の
一部をテスト集合とし、残りを訓練集合とし、訓練集合で訓練
を行い、テスト集合で汎化性能を評価する。
・k-分割交差検証法では、並列に処理を実行することで、計算時間
を最短で1/k程度まで短縮できる。
などがある。
3. モデルの学習を行うと、過剰適合や過少適合という状況になる場合が
ある。過剰適合、または過少適合している場合の対応として、
・決定木のモデルが過剰適合していたので、木の深さを浅くした。
・線形回帰のモデルが過剰適合していたので、正則化項を追加した。
・ランダムフォレストのモデルが過少適合していたので、特徴量 を
標準化した。
などがある。
4. 訓練を行う際、正則化 (regularization)という技法が用いられることが
ある。正則化は過剰適合を抑えることを目的にパラメータに何らかの
制約を課すことをという。
