
【新NISA】Excelで検討する新NISAの投資戦略:モンテカルロ・シミュレーションに挑戦(とりあえずやってみる)
さて、前回の記事("Excelで検討する新NISAの投資戦略:まずは標準正規乱数を発生させる" )で発生させた10,000 x 600の標準正規乱数を使って、今回は実際にExcelを使ってモンテカルロ・シミュレーションをしてみようと思います。
Excelシートの構成
幾つかの試行錯誤の結果ですが、とりあえず以下の図のような4つのシート構成に辿り着きました。
まずは、前回記事で発生させた10,000 x 600の標準正規乱数を"正規乱数値複写"シートに値複写。そして今回、つみたて枠(120万円/年)、成長枠(240万円/年)でそれぞれ投資対象が違うことを想定し、つみたて枠用のシミュレーションを"つみたて枠Calc"シートで、成長枠用のシミュレーションを"成長枠Calc"シートでそれぞれ実施。それらを"合計Calc"シートで合算する、という構成にしました。

いきなり課題に直面する
ここでいきなり基本的な課題に直面してしまいました。最初に、50年(600ヶ月)の期間のシミュレーションを10,000回試行する、ということを想定して10,000 x 600の標準正規乱数を発生させました。しかし、投資対象の枠がつみたて枠と成長枠の2つ、それぞれの枠で1つの投資対象としても、それぞれの時系列で同じ正規乱数を使うと、両方の時系列の相関が完全に1になってしまうということです。本来であれば、もし2つの投資対象を想定するのであれば、2つの対象の相関を仮定して、「あらかじめ定められた相関係数の2つの標準正規乱数の列」を取り出さないといけませんでした。
とりあえず今回は、つみたて枠でNYダウ、成長枠でNASDAQのインデックスに投資をするつもりでのシミュレーションをしようと思っていたので、相関は1ではないものの高そうなので、いったんこれで進めようと思います。
しかし、これは結構大事なポイントかと思います。今後どこかで再訪問して、再度相関を考慮したシミュレーションになるようにしたいと思います。
もう1つの課題ですが、Calcシートを作成し始めたらファイルがいよいよ重くなってきました。いくら標準正規乱数を関数のままではなく、値複写してきたとしても、"つみたて枠Calc"、"成長枠Calc"、"合計枠Calc"にはそれぞれ10,000 x 600個の計算式が入る形になります。ファイル上で何か動作をするたびに、数10秒、あるいは1分近くフリーズしてしまうことが増えてきました。とりあえず今回は力技で計算しちゃいましたが、今後相関を考慮した2組の標準正規乱数を使用することを考えると、シミュレーションについては試行回数を減らす、あるいは50年(600ヶ月)ではなく30年(360ヶ月)にしてみるなど、プロセスの簡略化も検討しないといけないですね。
"つみたて枠Calc"、"成長枠Calc"での計算
ではここで、"つみたて枠Calc"、"成長枠Calc"それぞれのシートの中身を見ていきます。基本的な計算コンセプトは"つみたて枠Calc"も"成長枠Calc"も同じですので、ここでは"つみたて枠Calc"シートを例に説明していきます。
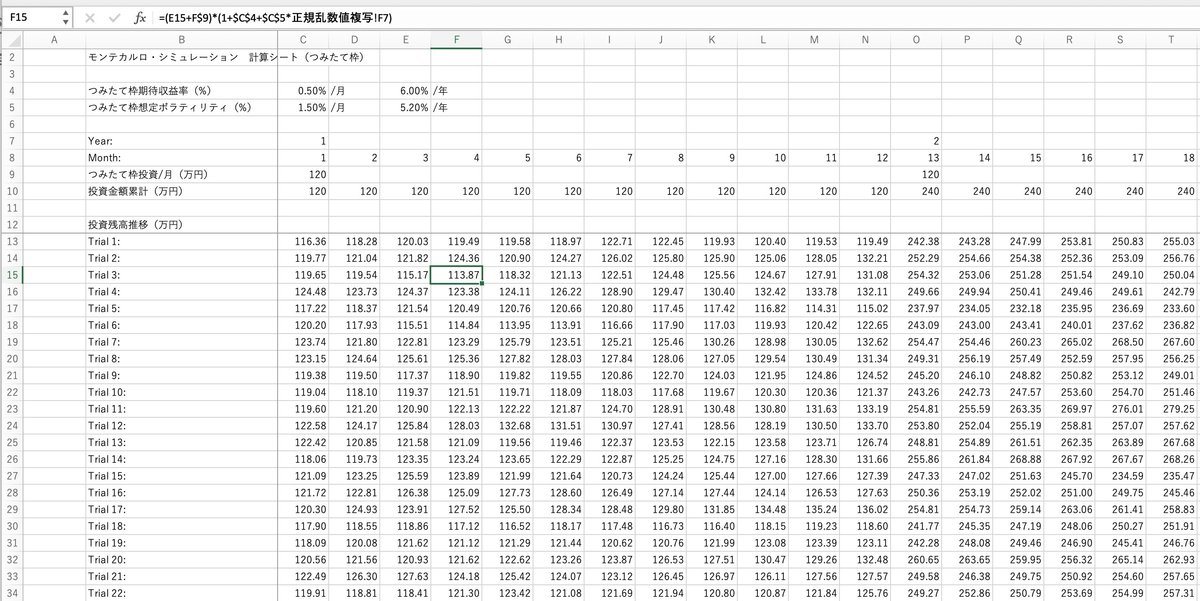
まずC4, C5のセルには、つみたて枠で投資をしようと思っている投資対象の想定期待リターン、想定ボラティリティを入れます。月次での計算を想定しているので、それぞれ月次ベースの数字を入れます。参考までにE4, E5列にはそれを年率換算したものを表示してます(期待収益率については単純に12倍した数字、ボラティリティはルート12倍した数字です)。
9行目には、つみたて枠に投資をする元本のプランが入れられます。とりあえず今は1年目の1月目に120万円の枠全額、2年目/13月目に2年目の120万円の枠全額、という感じで、それぞれの年の最初に枠の全額を投資をするように入れてます。もちろんここは今後さまざまな入金パターンでのシミュレーションができるようにしてあります。
そしてシミュレーションの計算式ですが、株価はこちらのWikipediaに説明されている幾何ブラウン運動に従うとして:
(当月末の運用残高)={(前月までの運用残高)+(当月の入金額)}x{1+(月次の期待リターン)+(月次のボラティリティ)x(標準正規乱数)}
として計算していきます(1月目だけは当月の入金額をそのまま使うだけですが)。上記シートは抜粋ですが、縦のTrialの行は10,000トライアルまで、そして横の時系列は600ヶ月まである膨大なシートとなってます。同様のコンセプトで"成長枠Calc"シートも作成、そしてそれらの合計のシートも作成しました。
今後の課題と方針
ここまでで今回のExcelを使ったモンテカルロ・シミュレーションの手順、計算過程はイメージできました。本来であれば、ここから「では10年後、20年後、30年後の運用資産はどうなっているのか?」という分布状況を確認、考察したいところですが、やはり以下の課題を整理することが先決かな、と思いました。
つみたて枠で1つの投資対象、成長枠で1つの投資対象と仮定し、それぞれの投資対象の相関を考慮した時系列でシミュレーションすべき(特定の相関のある標準正規乱数を発生させる
では、それぞれの枠での投資対象をどうするか?それぞれの期待リターンやボラティリティ、そして相関にどういう数字を使うかを推定する
ファイルがすでに重くなってきたので、まずは自分のこと(年齢はすでに54歳だし、月ごとではなく年ごとのシミュレーションで十分)を想定し、今後30年を3,000回試行する(3,000x30)程度でやってみる。回数や年月の拡張はその後にチャレンジする
相関のある標準正規乱数を発生させるためには、まずはつみたて枠、そして成長枠での投資対象の確定が先決ですね。次回ではまず、どういう投資対象にするか、そしてそれぞれの期待リターン、ボラティリティ、相関について議論したいと思います。
