
アキレスはカメを追い越す!
アキレスとカメという話があります。足の速いアキレスという人と、ノロノロ歩くカメがいます。アキレスは、カメの後ろにいて、前を歩いているカメを追いかけるようなかたちで、同じ方向に進んでいます。図にするとこんな感じです。
さて、ここでこのように考えます。
-アキレスが、カメがいた場所に辿り着く
-その時カメは、それよりも少し前に進んでいる
-さらにアキレスが、そのカメのいた場所に辿り着く
-その時カメは、それよりもさらに少し前に進んでいる
-またさらにアキレスが、そのカメのいた場所に辿り着く・・・
こう考えると、アキレスは永遠にカメに追いつきません。不思議ですよね?あり得ない話のはずですが、このように考えてみると、たしかにアキレスはカメに追いつかないのです。
しかし、この話を以下のように整理してみると、少しヒントが見えてきます。この話ではアキレスはカメに追いつかないとなっていますが、追いつくと仮定して、それまでの時間(T)を「1」として考えます。その時、アキレスのスピードがカメの2倍だとするとこんな感じになります。
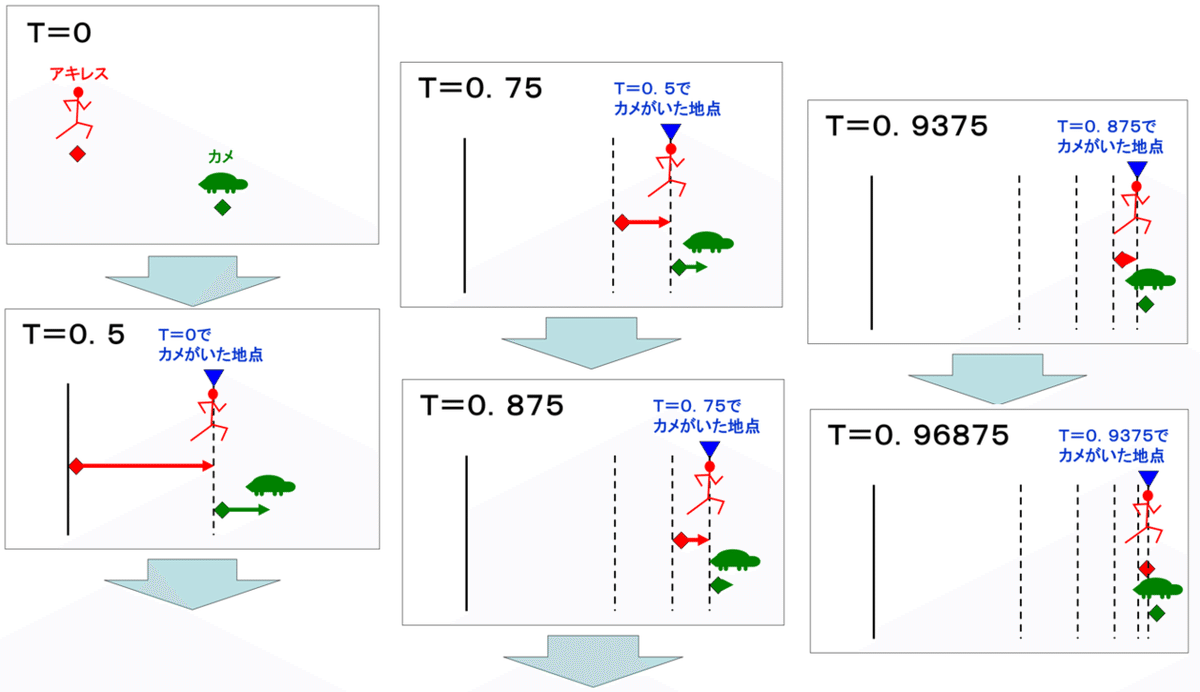
気付きましたでしょうか?
この話のポイントは、アキレスがカメに追いつくまでの「T」という時間を細かく刻んでいるだけの話だということです。Tの値は「0.9999・・・・・」といくらでも長くなります。この考え方をする限り、計算能力の高さは意味がありません。計算能力が高ければ高いほど、Tの小数点以下の9の数が増えるだけで、結局、「やはりアキレスはカメに追いつけない」という結論は変わらないのです。
では、なぜこのようなことが起こってしまうのでしょうか。それはこの話がアキレスがカメに追いつく地点までの論理で成り立っており、「アキレスがカメに追いつく前までの世界観」になっているからです。この思考をする限り、アキレスがカメを追い越す世界は存在しません。

しかし、私たちは、アキレスがカメを追い越すことを知っています。当たり前のように、アキレスがカメを追い越す先の地点が見えているわけです。でも冒頭の「アキレスとカメの話」を聞いたとき、あなたはアキレスがカメを追い越した先の世界が見えなくなっていたのではないでしょうか?問題は、こういうことが日常生活にも溢れているのではないかということです。
生きている中で、頭が良いだけでは解決できないことはたくさんあります。一所懸命頑張ればいいというものでもありません。むしろ頭が良くても、頑張って計算をしたとしても、「0.99」が「0.999」になるだけでは本当の答えにはたどり着かないということになってしまうのです。
ここで重要なのは、「仮説を置いてみる」ということです。上述の「アキレスとカメの話」でも、仮にアキレスがカメに追いつくとして、それまでの時間を「T=1」と仮定して検証しました。そこからヒントが見えたわけです。つまり、仮説を置くということが大切なのです。
目に見えている世界だけを追いかけても、永遠に答えにはたどり着かないことがあります。一度、計算を止め、頭を動かすのを止めてみて、目に見えない世界を考えてみてはいかがでしょうか。目に見えている世界にとらわれず、目に見えない世界について仮説を置いてみると、案外、それまで気付かない世界の存在に気付くかもしれません。
何のためにお金を稼いでいるの?何のために生きているの?といった根源的な問題に対するヒントも、そんなところにあると思います。
この記事が気に入ったらサポートをしてみませんか?
