
2 大気の熱力学(41/41問)仮公開
1 令和5年度第2回(通算61回)問3

知識事項の確認
大気の熱力学では、エマグラム上で表現される物理量について習熟している必要があります。詳細はお手元の参考書を通読して頂くとして、本問題を解くのに必要となる要点を簡単に紹介すると、
乾燥断熱変化では温位は一定
飽和水蒸気圧は気温によってのみ値が定まる
空気中で水蒸気が凝結すると熱が放出される
(a) の検討
持ち上げ凝結高度以下では乾燥断熱変化であるため、温位は変化しません。したがって「変化せず」となります。
(b) の検討
混合比は空気中の水蒸気が保存されていれば、当然変化しません。つまり、「も変化しない」が正解となります。
(c) の検討
空気塊が持ち上げ凝結高度を超えると、上昇に伴い空気中の水蒸気が凝結することになり、熱をまき散らしながら上昇することになります。したがって、温位は上昇することになります。したがって、「上昇し」が答えとなります。
(d) の検討
空気中の水蒸気が凝結すれば、当然混合比も減少します。つまり、「は減少する」が正解となります。
2 令和5年度第2回(通算61回)問4

解法の確認
フェーン現象の説明で見られる典型的な問題の様に見えますが、実は少し毛色が違います。一見すると山頂部で降水が発生しており、その為湿度は100%かと考えてしまいますが、それは間違いとなります。実は、本問では降水は生じません。
早速計算してみましょう。まず、空気解塊は下降後のふもとにおいて気温が30℃、相対湿度40%、更に表から飽和水蒸気圧が42hPaなので水蒸気圧は16.9hPaであると分かります。そして、これらの情報をもとに公式から混合比を求めると10.416g/kgであることが分かります。この混合比は断熱変化では保存されているため、頂上においても同じ値のはずです。
では、次に空気塊が山頂にあった時の状態について考察します。降下時は断熱変化であるので、気温は20℃であったことが分かります。もし、この時点で降水が生じており湿度が100%であったのなら、20℃の飽和水蒸気圧23hPaと混合比の公式から、混合比は15.84g/kgでなければなりません。しかし、先ほど計算した通り混合比は10.416g/kgです。足りていませんね。つまり、飽和していないのです。
さて、あとは相対湿度を計算するために、頂上での水蒸気圧と飽和水蒸気圧の比を求めればよいのですが、混合比の公式から、混合比と水蒸気圧は同一の大気圧下では比例することが分かります。つまり、わざわざ水蒸気圧で相対湿度を計算しなくても、混合比と飽和混合比の比から相対湿度を求めることができます。つまり、相対湿度は$${\dfrac{混合比}{飽和混合比}}$$となり、
$$
\dfrac{10.416}{15.84}\times100=65.8%
$$
となるので、答えは「③」となります。
3 令和5年度第1回(通算60回)問2
解法の確認
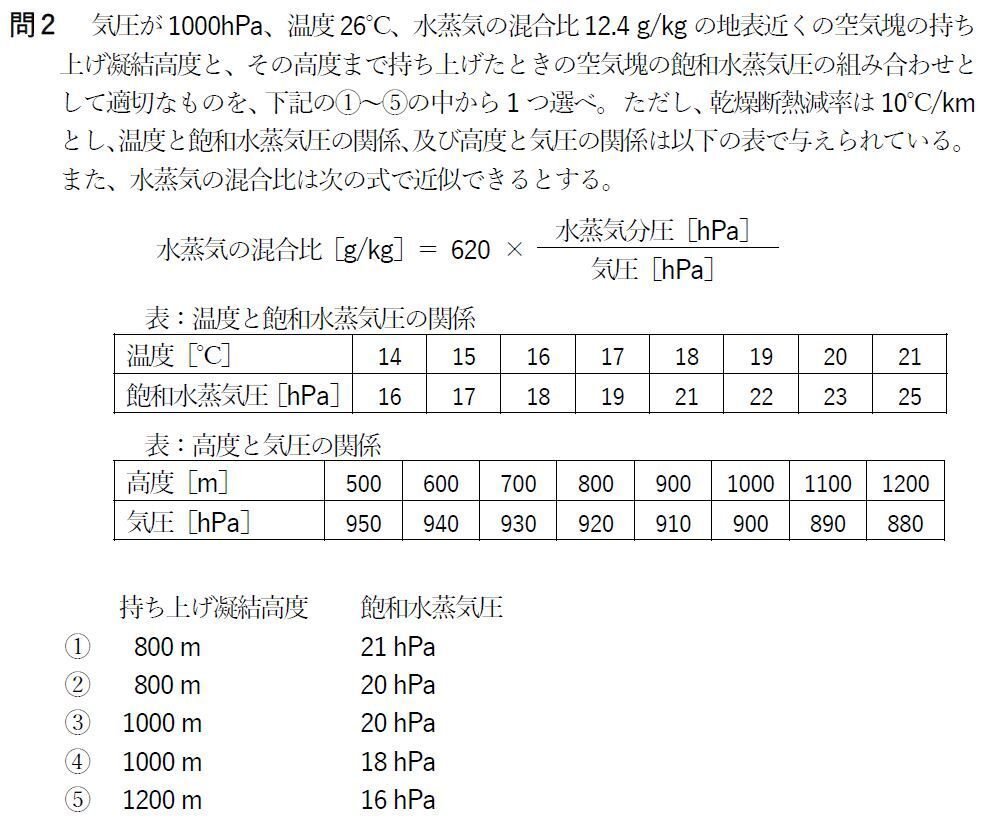
少々泥臭いですが、選択肢から矛盾の無い解答を絞り込んでみましょう。
まずは、ある高度で空気が飽和したと仮定します。
最初に800mと仮定すると、表から気圧は920となります。また、気温は18℃となるので飽和蒸気圧は21hPaとなります。これらの数値から、混合比を計算すると14.15g/kgとなります。しかし、これは地上での混合比よりも大きな値なので矛盾します。空気中の水分量が足りず、もっと高い高度でなければ飽和しないということですね。
次に1000mと仮定すると、気圧は900hPa、気温は16℃で飽和水蒸気圧が18hPaとなります。これらの結果をもとに混合比を計算すると12.4g/kgと、ぴったり地上での混合比と一致します。つまり、この高度で空気中の水蒸気が飽和したのです。
以上より「④」が正解です。
4 令和5年度第1回(通算60回)問3

解法の確認
大気圧とは、ある高度よりも上に存在する空気塊の質量で決まります。したがって、本問では黒枠内部の空気の質量を比較できれば良いのです。
この時点で、BとCは他の気柱と比較して併記温度が高いため、空気密度が低く質量が低いことが分かります。つまり、地上気圧は他よりも低くなります。
さて、BとCの比較ですが、上層の既に空気の薄い層で気温が上がったところで、気柱全体の質量には大して影響しません。一方で、最も空気の濃い下層で気温が変化すれば、質量の変化は大きくなります。
以上の考え方により、「B」が解答となります。
※本問は、気象予報業務センターの発表では、問題設定の不備によりすべての選択肢が正解となっています。私の考えでは、「大気の上端」が不明確であり、更に高度によって重力加速度が異なることから、厳密に比較することは本設問だけの条件では不可能という理由なのでしょう。恐らく、今後このような問題が出題されることはないか、あったとしてもかなり違った形になると思います
※「平成27年度第2回(通算45回)問1」に酷似した問題です。そちらの解説では「1 大気の構造」に分類していましたが、本解説では「2 大気の熱力学」として説明します
5 令和4年度第2回(通算59回)問2

知識事項の確認
湿球温度にまつわる問題は、筆者の経験上難問です。実際、本問は正答することはともかくとして、内容を完全に理解することは難しいと思います。現時点では内容が理解できなくても落ち込む必要はなく、十分に考えても分からないのであれば、捨てても良いと思います。実技や学科専門はもちろん、学科一般でも他にあまり関連する分野がないので、影響は最小限だと思います。
とりあえず、簡単に関連する知識事項をおさらいしたいと思います。
仮温度:ある湿潤空気と同じ圧力、同じ密度をもつ乾燥空気の温度
湿球温度:温度計に濡れたガーゼを巻いて測定したもの。水の蒸発により潜熱が奪われるため、乾球温度より低くなる。つまり、湿度によって蒸発量が変わるため、湿度を知る手掛かりになる
乾湿温度計の周辺の空気の混合比をw、同じく乾湿温度計の近傍の十分に水が蒸発した空気の混合比をw'とすると、w'の方が混合比は大きい。また、wを飽和混合比とする温度が露点温度で、w'を飽和混合比とする温度を湿球温度と言う
とにかくこの辺りは理解しにくいので、お手元の参考書を参照してきちんと理解できるようにしてください。
(a) の検討
かなり分かりにくい問題ですのでなるべくシンプルに言い換えましょう。T1は、w1を飽和混合比とする空気の温度です。つまり、T1は飽和状態の空気の温度になります。これは露点温度に他なりません。よって「誤」となります。
(b) の検討
知識思考でも説明した通り、設問における混合比w1とw2を比較すると、w2の方が値が大きい(湿ったガーゼを通過している)ので、それぞれの混合比を飽和混合比とする温度(順に露点温度、湿球温度)も後者の方が大きいことが分かります。よって、「正」となります。
※気温が高いほうがより多くの水蒸気を抱えることができる、というイメージです
(c) の検討
左辺は単位質量当たりの潜熱と混合比の差の積であり、水の蒸発分のエネルギーを表しています。そして右辺ですが、同じ量に相当するエネルギーの差を、気温変化とその比例定数(この場合は定圧比熱ですね)の積によって表現しています。同じエネルギー量を異なる方法で計算しているのですから、右辺も左辺も同じ値になります。したがって、「正」であることが分かります。
6 令和4年度第2回(通算59回)問3

解法の確認
一見すると難しい問題ですが、計算の必要はなく簡単に解けます。
今回覚えておくべき事項は、水蒸気の密度は乾燥空気よりも小さいということです。つまり、湿度の高い空気は同温同圧の乾燥空気と比べて密度が低いのです。
さて、各地点の気圧を比較するのが本問の目的ですが、気圧とはその高度より上にどれだけの質量の空気が存在するかです。本問では、高度1000mの気圧となっていますが、与えられた平均気温は地上から1000mまでの値となっています。そして、地上気圧は全ての地点で等しいとされています。
つまり、地上気圧が等しい以上、どの地点でも上空に存在する空気の質量は等しいのです。そうすると、地上から1000mに存在する空気の質量が小さければ、その分1000m以上に存在する空気の質量が大きいことになり、高度1000mの気圧は大きいと言えます。これは重要です。今回の問題では、最初に地上から高度1000mまでの空気の質量が最も小さい地点を考える必要があります。
さて、地上から高度1000mまでの空気の平均気温は、BとC地点がともに等しく高い値になっています。つまり、地点BとCの地上から高度1000mの空気の密度は地点Aよりも小さくなることになります。この時点で、$${P_A}$$が最小であると分かります。
次に地点$${P_B}$$と$${P_C}$$ですが、Cの方が混合比が高いので、水蒸気量が多いことが分かります。実際、空気中の水蒸気の体積比は0~2%程度と僅かなので、湿度による空気密度の変化は、空気そのものの温度による密度変化に比べると極めて小さいのですが、それでも変化自体は存在します。少し話が逸れましたが、Cの混合比が最も高い以上、僅かですが地点A、Bよりも地点Cの方が地上から高度1000mまでの空気の密度が小さいことになります。
長くなりましたがあと一歩です。地上から高度1000mの空気の平均密度で比較した場合、順にAが最大でCが最小になります。前述の説明の通り、これを高度1000mの気圧に置き換えたら、$${ P_A< P_B < P_C}$$となりますので、「①」が正解です。
7 令和4年度第1回(通算58回)問2

知識事項の確認
いくつかの公式を覚えていれば簡単に解ける問題です。
まず、普遍気体の状態方程式を紹介します。これは覚えておくと役に立ちます。
$$
P = ρ\dfrac{R^*}{M}T
$$
$${R^*=8314 [JK^{-1} kmol^{-1}]}$$となります。そしてこの値が重要です。$${M}$$に期待の分子量を代入すると、その気体の気体定数が求められるのです。
次に水蒸気密度の公式です。
$$
ρ_v=\dfrac{0.217e}{T} [kgm^{-3}]
$$
$${e:水蒸気圧 T:気温}$$
これにより、単位体積当たりの水蒸気の質量が求められます。
(a) の検討
普遍気体の状態方程式より、$${水蒸気の気体定数=\dfrac{8314}{18}=462 [Jkg^{-1} K^{-1}]}$$となります。「462」が解答です。
(b) の検討
設問より、27℃の空気の飽和水蒸気圧は36hPaです。今考えている湿潤空気の相対湿度は50%なので、水蒸気圧は18hPaです。したがって、水蒸気密度の公式を利用すると、
$$
ρ_v=\dfrac{0.217\times18}{300} =0.013 [kgm^{-3}]
$$
となります。
以上より「③」が解答です。
8 令和4年度第1回(通算58回)問3

解法の確認
比較的簡単な計算問題ですので、特別な知識は必要ありません。
まず、Aに含まれる水蒸気の量を単位として、Bに含まれる水蒸気量を計算すると、Bの体積はAの2倍で混合比も2倍の2qとなります。したがって、Bには4個単位の水蒸気が含まれています。
さて、AとBの空気塊を混合すると、水蒸気量は5個単位、体積はAの3倍になります。したがって、混合比は$${\dfrac{5q}{3}}$$となり、解答は「③」となります。
9 令和3年度第2回(通算57回)問3

知識事項の確認
条件付き不安定の状態にある大気の気温減率は、乾燥断熱減率と湿潤断熱減率の間の値である、ということを知っていれば簡単に解ける問題です。
(a) の検討
高度500mの気温が20℃ですので、乾燥断熱減率と湿潤断熱減率で気温が変化した場合、高度1500mでは10~15℃の範囲になることが分かります。よって、①か③に絞れます。
(b) の検討
高度1000mで持ち上げ凝結高度になるということは、この高度500mにある空気塊は1000mまで乾燥断熱減率で温度が変化することになります。一方で、高度500~1500mまでの大気は条件付き不安定で気温減率は一定です。つまり、500mの空気塊は周囲の大気より冷たく重くなります。なので、下降することになります。よって、「②」が正解です。
※気象業務支援センターによると、本問題は解なしとなっています。理由は、問題設定では(a)の解答では高度1500mの気温に10℃が含まれてしまっています。つまり、500~1500mの大気がぴったり乾燥断熱減率で気温変化している場合も含まれてしまっているのです。その場合、高度500mの空気塊も乾燥断熱減率で変化するため、周囲の温度と厳密に等しい温度変化をしてしまい、上昇も下降もせず中立状態になります。
10 令和3年度第2回(通算57回)問4

知識事項の確認
エマグラム上に表現される物理量の性質を理解していれば解ける、基本的な問題です。乾燥断熱減率や湿潤断熱減率、温位、相当温位、飽和水蒸気圧についてしっかりと理解しておきましょう。
(a) の検討
湿潤断熱過程ということなので、空気中の水蒸気が凝結しながら周囲に潜熱をまき散らしていることになります。したがって、温位はどんどん上昇しますが、相当温位はそもそも温位に気体中の水蒸気のエネルギーを加味した概念なので、これは保存されます。温位は上昇、相当温位は一定となり「誤」であることが分かります。
(b) の検討
湿潤断熱減率は一定です。なので、高度に関わらず概ね5.0℃/kmで変化します。よって、「誤」となります。
(c) の検討
飽和水蒸気圧は気温によってのみ定まる値です。よって、「誤」となります。
(d) の検討
乾燥断熱減率は一定です。なので、高度や気圧に関わらず概ね10℃/kmで変化します。よって、「正」となります。
11 令和3年度第1回(通算56回)問2

解法の確認
方程式を立てることができれば簡単な問題です。
まず、持ち上げ凝結高度を$${x}$$とします。高度3kmまでに$${25-5=20℃}$$気温が低下します。そして、そのうち$${x}$$kmは乾燥断熱減率10℃/kmで温度が低下します。そして残りの$${3-x}$$kmは湿潤断熱減率5℃/kmで温度が低下します。これをもとに方程式を立てましょう。
$$
25-5=10x+5(3-x)
$$
これを解いて、$${x=1}$$となります。また、持ち上げ凝結高度での気温は$${25-10\times1=15℃}$$となります。
以上より「②」が解答となります。
12 令和3年度第1回(通算56回)問3

知識事項の確認
飽和水蒸気圧は気温にのみ依存します。親の顔を忘れても、このことは覚えておきましょう。また、飽和混合比は混合比の公式から求めましょう。
$${w=0.622\dfrac{e}{p}[kg/kg]}$$(e:水蒸気圧 p:大気圧)
(a) の検討
Aと同じ気温です。つまり、同じ飽和蒸気圧となりますので「誤」となります。
(b) の検討
混合比の公式を眺めてみましょう。この公式の水蒸気圧が飽和蒸気圧になった場合、左辺は飽和混合比となります。
$${w=0.622\dfrac{e}{p}[kg/kg]}$$
同じ気圧なら、飽和水蒸気圧が大きい方が飽和混合比も大きくなることが分かります、したがって、「正」となります。
(c) の検討
再度、混合比の公式を眺めてみましょう。
$${w=0.622\dfrac{e}{p}[kg/kg]}$$
同じ蒸気圧なら、分母の気圧が大きい方が飽和混合比は小さくなることが分かります、したがって、「誤」となります。
13 令和2年度第2回(通算55回)問2

解法の確認
このパターンの問題は、まず持ち上げ凝結高度を求める必要があります。そのためには混合比を求める必要があります。なぜ混合比が重要かというと、混合比は持ち上げ凝結高度までは保存される量であり、更に混合比の公式からある気圧(つまり高度)での蒸気圧を求めることができるからです。そして求めた蒸気圧がその気温での飽和水蒸気圧と比較してどういう関係にあるかが重要になります。
それでは、標高0mでの混合比を計算してみましょう。
$$
w=\dfrac{622\times(31.7\times10^2\times0.5)}{1000\times10^2}=9.86 [g/kg]
$$
さて、標高1000mでは気圧が900hPaであり、持ち上げ凝結高度以下であれば、乾燥断熱減率で温度変化したため気温は15℃のはずです。この条件で、飽和混合比を求めてみると、
$$
w=\dfrac{622\times(17.0\times10^2)}{900\times10^2}=11.75 [g/kg]
$$
となりました。つまり、問題の空気塊は標高1000mではまだ飽和しないことになります。
それでは、混合比と飽和混合比から直接相対湿度を計算すると、
$$
\dfrac{9.86\times100}{11.75}=83.9 [%]
$$
となり、丸め込むと84%なので「③」が正解です。
14 令和2年度第2回(通算55回)問3

知識事項の確認
不意を突くような問題ですが、冷静に考えれば大したことはありません。
(a) の検討
熱力学第一法則は、加えた熱量は仕事と内部エネルギーの増加量の和に等しいということでした。つまり、断熱的に膨張する(加えたエネルギーがゼロ)と内部エネルギーは減少する、つまり温度が下がるということですね。
そして、静力学平衡の式では、高度によって気圧が下がること、つまり気体が膨張することを計算できます。
以上のことより、気体が上昇することで気圧が下がり(つまり膨張し)、外部に対して仕事をすることで、内部エネルギーが減少することを計算できることが分かります。これは乾燥断熱減率に他なりません。
(b) の検討
温度風は、平均温度の異なる空気塊の間に生じた気圧差によって生じた風が根底にあります。各高度に応じて気圧傾度が異なるため、高度に応じて風向や風速が変化します。そして温度風は、下層の風と上層の風のベクトルの差分として定義されます。つまり、高度に応じた気圧傾度を計算する必要があり、地衡風平衡の関係に加え静力学平衡の式も必要になります。
以上のより解答は「①」となります。
15 令和2年度第1回(通算54回)問2

解法の確認
湿潤空気中の水蒸気の分圧を計算し、湿潤空気の気圧から引くことで乾燥空気の分圧が求まります。基本的な問題なので必ず解けるようになりましょう。
それでは、水蒸気の状態方程式を立ててみます。
$$
P_w=(26\times10^{-3}\times0.5)\times461\times300=17.97\times10^{2} [Pa]=18 [hPa]
$$
飽和水蒸気密度の単位に注意してください。気体定数に合わせてkgに変換する必要があります。また、Pa(パスカル)とhPa(ヘクトパスカル)についても、慣れない方はきちんと忘れずに変換してください。気象予報士試験で用いられる各種公式に、直接hPaを用いるものはありません。
さて、あとは湿潤空気の気圧から求めた水蒸気圧を引けば、乾燥空気の分圧になります。$${1008-18=990 [hPa]}$$なので、解答は「④」となります。
16 令和2年度第1回(通算54回)問3

知識事項の確認
温位や混合比、飽和蒸気圧等のこの分野の基本的な物理量に関する知識を確認する良い問題です。難しい部分はないので、自信がない方はきちんと理解できるようにしてください。
さて、折角なので温位の公式について紹介します。
$$
θ=T(\dfrac{P_0}{P})^{0.286}
$$
この公式は近似式ですが、気象予報士試験ではこれ一つ覚えておけば、温位に関する問題で判断に困ったときに頼れます。左辺の$${θ}$$は温位で、右辺の括弧内分子の$${P_0}$$は1000[hPa]で、同じく分母の$${P}$$は気圧です。
(a) の検討
飽和するまでは、空気塊は乾燥断熱減率で温度を変化させます。一方で温位は保存されます。したがって「正」となります。
(b) の検討
混合比の定義は、単位体積当たりの水蒸気の質量です。AからBに至る過程では、凝結はありません。つまり、混合比は保存されます。よって「正」である。
(c) の検討
相当温位は、ある空気塊の温位に対して、更に水蒸気の潜熱分のエネルギーを加味した物理量です。したがって、乾燥断熱過程でも湿潤断熱過程でも保存される量です。よって「正」となります。
(d) の検討
感覚や直感などには頼らずに、さっさと温位の公式に頼って考えてみましょう。
$$
θ=T(\dfrac{P_0}{P})^{0.286}
$$
Cより上の高度で空気塊が降下するのであれば、周囲の大気よりもこの空気塊は温度が低くなります。
上記公式について、右辺の$${(\dfrac{P_0}{P})^{0.286}}$$部分に注目します。Cより上の高度における空気塊と周囲の大気を比較してみましょう。同じ高度であれば気圧が等しいので、注目部分は空気塊と周辺の空気で同じ値になるので、以下の様な方程式を立てられます。
$$
\dfrac{θ_{空気塊}}{T_{空気塊}}=\dfrac{θ_{大気}}{T_{大気}}
$$
これを変形して、
$$
\dfrac{T_{大気}}{T_{空気塊}}=\dfrac{θ_{大気}}{θ_{空気塊}}
$$
さて、Cより上の高度では空気塊の方が温位が大きいので、
$$
\dfrac{T_{大気}}{T_{空気塊}}=\dfrac{θ_{大気}}{θ_{空気塊}} < 1
$$
つまり、空気塊の方が温度が高く、そのため空気塊には浮力が働くはずです。よって「誤」となります。
17 令和元年度第2回(通算53回)問1

知識事項の確認
あまり難しい問題ではありません。
(a) の検討
乾燥空気の密度といのは、つまるところ大気圧に他ならない。つまり、鉛直方向で一定ではなく、上層ほど値は小さくなります。したがって「誤」となります。
(b) の検討
熱帯地域の500hPaの方が気温が高いため、当然乾燥空気の密度も低くなります。したがって「正」となります。
(c) の検討
水蒸気の密度を考える前に、大気中の水蒸気が占める体積比を思い出しましょう。高々数%だったと思います。つまり、どう比較したところで、乾燥空気の密度には適いません。したがって「誤」となります。
18 令和元年度第2回(通算53回)問2

知識事項の確認
困ったら公式に頼りましょう。その方が確実で正確です。
(a) の検討
温位の公式をもとに判断しましょう。なお、$${P_0=1000 [hPa] }$$です。
$$
θ=T(\dfrac{P_0}{P})^{0.286}
$$
設問の内容は、左辺の温位が右辺の温度よりもいかなる空気圧においても高い、ということです。
公式を眺めると、$${P>P_0}$$の時右辺の$${(\dfrac{P_0}{P})^{0.286}}$$が重要になります。もし、右辺の括弧部分が1よりも小さければ、温位は空気塊の温度よりも小さくなります。そして、もしも(\dfrac{P_0}{P})^{0.286}の気温Tが1000hPaよりも大きければ、括弧内は1よりも小さくなります。よって、「誤」となります。
(b) の検討
相当温位は、その空気塊に含まれる水蒸気のエネルギーを温位に加味した量です。したがって「正」となります。
(c) の検討
乾燥断熱過程では温位は保存します。したがって「正」となります。
(d) の検討
湿潤断熱過程では温位は上昇します。上昇に伴い水蒸気が凝結し、潜熱をまき散らすイメージでしたね。したがって「正」となります。
19 令和元年度第2回(通算53回)問5

解法の確認
気圧を問われたら、空気の質量を考えるのが自然な発想です。ここまで解いてきたのであれば、そろそろこの発想が身についてきたと思います。
高度1000mでの気圧は全ての地点で等しいので、高度1000m以下の空気について考えます。空気の質量を考える上で必要なのは密度ですが、それは気温によって決まります。つまり、本問題では高度1000m以下の平均気温の大小を比較するのです。
平均気温が最も低いのは地点Aであることはグラフから分かります。また、地点BとCを比較すると、Bの方が平均気温が低いことが分かります。
以上より、地点Aが最も平均気温が低く、空気の密度は最も高くなり、質量も最大となります。地点Cはその逆で。質量が最小となります。よって、「⑤」が正解です。
20 令和元年度第1回(通算52回)問2

知識事項の確認
そろそろこの「仮温度」なる概念と向き合う時が来ました。仮温度は、頻度が少ないのですが出題されることのある物理量で、私も苦手でした。
まずは教科書的に覚えておきましょう。
「ある湿潤空気と同じ気圧と密度をもつ乾燥空気の温度を仮温度という」
なぜ仮温度が必要になったかというと、湿潤空気に対しても、乾燥空気と同じ気体訂正を用いて状態方程式を立てたいからです。湿潤空気は、通常であれば水蒸気が含まれるので気体定数はその分だけ乾燥空気と異なってしまいます。そこで、先に定義した通りの温度を代わりに用いると、乾燥空気と同じ状態方程式を使えるのです。
さて、仮温度は気温よりも高くなります。理由は、湿潤空気の方が乾燥空気より密度が低い(忘れた方は思い出してください。「令和4年度第2回(通算59回)問3」の解説を参照のこと)からです。乾燥空気の方が密度が大きいので、その分少し気温を上げて密度を下げないと密度が等しくならないからです。
(a) の検討
仮温度の定義から「密度」が正解であると分かります。
(b) の検討
知識事項で説明した通り、湿潤空気は乾燥空気よりも軽くなるので、乾燥空気がその湿潤空気と同じ密度になるためには少し気温を上げる必要があります。したがって「高い」となります。
(c) の検討
一瞬うろたえそうですが、何てことはありません。仮温度が高いということは、それだけ実際の大気(湿潤空気ですね)の水蒸気量が多く、そのため密度が低いのです。そしていい加減聞き飽きたかも知れませんが、大気圧を考えるときは、その地点より上にある空気の質量を考えれば良いのです。密度が低いのですから、当然質量は軽くなりますね。ということで「低い」となります。
21 令和元年度第1回(通算52回)問3

解法の確認
フェーン現象に関する頻出のパターンですが、今回は計算問題ではなく定性的な判断ができれば問題ありません。
まず、山を越える際に空気中の水蒸気が凝結することで空気が加熱され、結果として山を越えて麓にたどり着くころには元々の気温よりも高くなっている、ということがフェーン現象の本質でした。
そうなると、どれだけ多くの水蒸気が凝結したかが、実際の昇温量を決めます。そして重要なことは、飽和蒸気圧曲線は文字通り曲線ですが、大気の下層付近では飽和蒸気圧曲線ほぼ直線と見なせるということです。
ということは、大気の下層ではほぼ高度に比例して直線的に飽和蒸気圧が減少します。したがって、飽和蒸気圧に比例する飽和混合比(空気中の水蒸気量でしたね)も、高度に比例して直線的に値が減少します。
以上の議論より、本設問における高度帯では、飽和した高度から頂上までの高度差に比例した量だけ水蒸気が凝結するのであり、その量に比例して温度が上昇するのです。ということは、高度差の順に温度を並べれば良く、「③」が正解となります。
22 平成30年度第2回(通算51回)問3

解法の確認
「令和4年度第1回(通算58回)問2」と酷似した問題です。まずは普遍気体の状態方程式について思い出してみましょう。
$$
P = ρ\dfrac{R^*}{M}T
$$
$${R^*=8314 [JK^{-1} kmol^{-1}]}$$
(a) の検討
普遍気体の状態方程式によると、気温と気圧が一定であれば、分子量が大きくなると密度も比例して大きくなる必要があることが分かります。そうでないと、等号が成立しません。よって、「比例して」が正解です。
(b) の検討
混合比の公式を覚えていれば即答できます。こういう問題を見かけたらラッキーだと感じるようになってください。
くどいですが、
$$
w=622\dfrac{e}{p}[g/kg]
$$
(e:水蒸気圧 p:大気圧)
でした。代入すると、
$$
w=622\dfrac{42\times10^2}{1000\times10^2} = 26.124[g/kg]
$$
となるので、最も近い値は「27」となります。
23 平成30年度第2回(通算51回)問4

知識事項の確認
エマグラム上で空気塊の変化を考える基本的な問題です。ここまで解いてきたのであれば、既に楽に解けるようになっているはずです。もしも解けなかったとしても、諦めずに何度も解きなおしてください。
(a) の検討
凝結するまでは、当然乾燥断熱過程です。よって、「乾燥断熱線」が正解です。
(b) の検討
露点温度とは、空気が飽和する温度です。つまり、エマグラム上では「等飽和混合比線」上で表現されます。
(c) の検討
凝結後は湿潤断熱過程です。つまり、「湿潤断熱線」が正解です。
24 平成30年度第1回(通算50回)問2

知識事項の確認
温位と相当温位に関する理解が必要な問題です。既に散々似たような問題を解いていますが、一度厳密な定義を読んで理解を深めてみましょう。
「温位とは、乾燥した空気塊を1000hPaの高度まで断熱的に移動させたときの空気塊の温度(K)である」
「相当温位とは、ある空気塊を断熱的に移動させ、内部に含まれる水蒸気を全て凝結させて、その後1000pHaの高度まで断熱的に移動させたときの空気塊の温度(K)である」
温位の方はイメージしやすいはずです。これは、異なる高度の空気塊を基準となる高度である1000hPaまで断熱的に移動させて比較するための考え方です。1000hPaで温度が高くとも、500hPaまで上昇させたら温度は下がります。異なる高度の空気塊を比較するには、共通の高度にまで断熱的に移動させないと意味がありません。そして断熱的に移動させるときは、全て乾燥断熱過程として扱うのです。
相当温位は、温位の概念に水蒸気の持つエネルギー(潜熱)を加えた概念です。空気中に含まれる水蒸気にはエネルギーがあり、これは潜熱と呼ばれます。そしてその水蒸気のエネルギー(潜熱)は、凝結する際に放出されて空気塊の温度を上げます。相当温位では、空気塊に含まれる水蒸気のエネルギーを全て温度に変換して、その上で異なる空気塊の温位を比較するのです。
(a) の検討
同じ700hPaで同じ270Kの気温です。これを乾燥断熱過程によって1000hPaに移動させても、空気塊A及びBは同じ温度のままです。つまり、温位は等しいので「誤」です。
(b) の検討
空気塊AとCは気温も気圧も等しいですが、湿度はCの方が大きいです。温位であればAとCはどちらも等しいのですが、相当温位は温位に水蒸気のエネルギー(潜熱)をさらに加えた量なので、Aの相当温位の方がAの温位(=Cの温位)よりも大きな値になります。よって、「誤」となります。
(c) の検討
空気塊BはCと湿度以外は全て等しいですが、湿度はBの方が低い値です。つまり、水蒸気の量が小さいので、その分相当温位は小さくなります。よって、「正」となります。
(d) の検討
空気塊Cの方が、Dよりも気圧が低いのに温度は同じです。つまり、より上空にあるのにCはDと同じ気温です。ということは、Cの方が温位が高くなるのです。よって、「誤」となります。
25 平成30年度第1回(通算50回)問3

知識事項の確認
「令和2年度第2回(通算55回)問3」と類似の問題です。
(a) の検討
公式を覚えていれば一目で間違いだと分かります。静水圧平衡の式は以下の通りです。
$$
\varDelta P= – \rho g\varDelta Z
$$
(b) の検討
以下は理系の方向けの説明になります。残念ですが、私の能力では数式なしで説明できません。
ここで何をしたいかと言いますと、層厚を大気の密度を用いずに式で表すことです。なぜ層厚が必要かと言いますと、層厚はその層の平均気温に比例するからです。つまり、層厚を大気密度に依存しない形で表現すれば、平均気温も同時に表現可能になるのです。
まず、気体の状態方程式を考えます。
$$
P=\rho RT
$$
大気の密度$${ρ}$$を消したいので、これを直接抜き出すと、
$$
\rho=\Large{\frac{P}{RT}}
$$
次に、静水圧平衡の式を考えます。この式にも大気の密度$${ρ}$$が使われています。
$$
\varDelta P= – \rho g\varDelta Z
$$
これの$${ρ}$$に先ほどの式を代入すると、
$$
\varDelta P =-\Large{\frac{P}{RT}} \normalsize{\times g\varDelta Z}
$$
ここで右辺に出てくるTは、その気層の平均気温だと考えられます。つまり、設問の通り平均気温と$${\varDelta P}$$の関係を説明できています。よって、熱力学の第一法則ではなく気体の状態方程式が正しく、「誤」となります。
※やや苦しい説明ですが、熱力学の第一法則には気温Tが出てこないということを理由に「誤」と判断できなくもありません
(c) の検討
散々書いていますが、気圧とはその地点より上層の空気の質量に比例します。今回の場合、高度Hの気圧は等しいので、高度H以上の空気の質量は2地点で等しいことになります。そうすると、地上から高度Hまでの空気の質量がポイントになります。この部分の平均温度が高い方が、密度が小さくなり、質量も小さくなるはずです。つまり、「誤」となります。
本問は(b)が難しいと思います。しかしながら、(a)と(c)は瞬時に誤と分かる簡単な設問になっています。そうすると、消去法で正解が導けます。しかし、気象予報試験対策においては、消去法に頼った結果の正解は誤答と見なすべきです。消去法に頼るのは本番だけです。
26 平成29年度第2回(通算49回)問2

解法の確認
ラジオゾンデを例に挙げた問題でしょうか。「令和3年度第1回(通算56回)問1」と類似の問題です。
計算問題ですが、難しく考えずに気体の状態方程式を利用すれば良いのです。苦手な方は、諦めて心に刻まれるまで繰り返し解いてください。
$$
PV = nRT
$$
これを、n(mol数)について解いた形に変形します。
$$
n= \dfrac{PV}{RT}
$$
重要なのは、気球の中にある気体の量は変化しないので、nは一定であるということです。
早速、上の式に地上で与えられた諸元を代入してみましょう。
$$
n= \dfrac{1000\times10^2\times 4}{R\times 300}
$$
破裂する高度では体積が$${300m^3}$$になるので、
$$
n= \dfrac{P_b\times 300}{R\times T_b}
$$
となります。
それでは両辺を等号で結ぶと、
$$
\dfrac{1000\times10^2\times 4}{R\times 300}=\dfrac{P_b\times 300}{R\times T_b}
$$
これを変形すると、
$$
\dfrac{P_b}{T_b}=\dfrac{40}{9}=4.44
$$
選択肢の中から、$${\dfrac{P_b}{T_b}=4.44}$$となるものは「②」の高度30kmとなります。
27 平成29年度第2回(通算49回)問3

知識事項の確認
K-indexという量に関する定義は、恐らく知らない方が多いと思います。しかし、似たような指数にショワルター安定指数(SSI)というのがあり、こちらは対流性の降水、つまり雷雨の発生に関する指標として利用されています。
本問題は、k-index知らなくても解けるようになていますので安心してください。初めて見る問題でも、大抵の場合は解けるようになっていますし、そうでなくとも選択肢を絞り込むことはできます。
まず設問を読んでみると、k-indexとは水蒸気量に多寡に関する指標で、水蒸気が多いほどk-indexの値も大きくなることが分かります。これだけ抑えておけば全ての設問に答えることができます。
(a) の検討
露点温度が高い方が湿度が高い、つまり水蒸気量が多いことになります。なので、k-indexの性質を考えれば「-」が正解だと分かります。
(b) の検討
k-index中の$${(T_{850}-T_{500})}$$は、850hPaと500hPaの温度差になります。気温減率が大きいほど、この値は大きくなります。よって、「気温減率」が正解です。
(c) の検討
一瞬躊躇しますが、層状性降水とは温暖前線によって発生する層状の雲(乱層雲が多いそうです)から生じる降水で、これは前線を構成する寒気の上を滑って緩やかに上昇する暖気によるものです。
一方で、雷雨とは対流性の雲によってもたらされる降水現象(しゅう雨)です。k-indexに似た指数であるショワルター安定指数(SSI)も、対流現象の発生のしやすさに関する指標でした。したがって、k-indexも「雷雨」発生に関する目安と言えます。
28 平成29年度第1回(通算48回)問2

知識事項の確認
湿球温位という見慣れない物理量が出てきますが、何てことはありません。温位が空気塊を乾燥断熱過程によって1000hPaに移動させるのに対して、湿球温位はこれを湿潤断熱過程にしただけです。
湿潤断熱減率は乾燥断熱減率よりも値が小さいので、持ち上げ凝結高度にある空気塊の温位と湿潤温位を比較すれば、温位の方が値が大きくなります。また、蛇足ですが相当温位は温位よりも水蒸気のエネルギー(潜熱)の分だけ値が大きくなります。
(a) の検討
既に説明した通り、相当温位が一番大きく、湿潤温位が一番小さい値になります。よって、「$${θ_W<θ<θ_e}$$」が正解となります。
(b) の検討
温位は、空気塊が飽和してしまうと値が保存されません。一方で相当温位や湿潤温位はそもそも湿潤断熱過程ですので、影響はありません。よって、「$${θ_eとθ_W}$$」が正解になります。
29 平成29年度第1回(通算48回)問3

知識事項の確認
本問題は、典型的な対流不安定(ポテンシャル不安定)の説明です。
これは、ある気層の上端と下端について注目した時、気層そのものを持ち上げた場合その上端と下端で温度変化が異なることにより発生します。図にある線分ABの傾きと、A’B’の傾きが変化するということです。
より詳しく説明すれば、気層の上端と下端を結んだ直線(図ではAB)が垂直に近いほど、大気は安定になります。更に言えば、傾きが正の値であれば絶対安定な逆転層(上層ほど温度が高い)になります。
反対に、傾きが水平に近いほど気層は不安定になります。理由は、上層ほど温度が低いからです。つまり、このような気層に空気塊を放ち、上層に持ち上げると、空気塊よりも周りの気層の気温減率の方が大きくなってしまい、空気塊が上昇するにつれてますます浮力を得て上昇を続けてしまい、対流現象が発生するからです。
さて、設問に戻りますが、A→A’の変化は「最初に乾燥断熱過程でその後は湿潤断熱過程」になるべきです。B→B’の変化は「常に乾燥断熱過程」となります。そうすることによって、線分ABの傾きとA’B’の傾きが上記の説明の通りになります。よって、「②」が正解になります。
30 平成28年度第2回(通算47回)問2

解法の確認
普遍気体の状態方程式を利用すれば問題ありません。AとBは体積が等しいので、密度の比較をすれば気体の質量を比較できます。
$$
P = ρ\dfrac{R^*}{M}T
$$
$${R^*=8314 [JK^{-1} kmol^{-1}]}$$
これをAとBそれぞれに対して密度ρについて解くと、
$$
ρ=P\dfrac{M}{R^*T} =1000\times10^2\dfrac{29}{8314\times300}=1.163
$$
$$
ρ=P\dfrac{M}{R^*T} =29\times10^2\dfrac{18}{8314\times300}+971\times10^2\dfrac{29}{8314\times300}=1.15
$$
以上より、AとBの密度を比較すると「容器B内の気体の方が約1%軽い」ことが分かる。
31 平成28年度第2回(通算47回)問3

解法の確認
まず、相対湿度ですがこれは簡単です。空気塊を持ち上げると、やがて持ち上げ凝結高度に達します。つまり、相対湿度が100%になるからです。つまり、相対湿度は「増加する」が正解です。
次に水蒸気密度です。残念ながら、公式では結論を出せません。
しかし、考え方としてはシンプルです。飽和混合比は気温とともに下がります。そして、飽和水蒸気密度とは単位体積当たりの水蒸気の質量の最大値でした。つまり、飽和水蒸気密度も飽和混合比と同様に気温が低下すると値が低下することが分かります。
さて、水蒸気密度は飽和水蒸気密度よりも値が小さいので、飽和水蒸気密度が低下すれば、水蒸気密度も同様に低下すると言えます。つまり、水蒸気密度は「減少する」となります。
最後に比湿です。これはほぼ混合比と同じ値になります(必ず覚えておいてください)。そして混合比とは単位体積あたりの水蒸気の質量です。これは乾燥断熱過程であれば保存する量です。よって、「一定である」が正解となります。
最後に一言ですが、この問題は簡単ではありません。公式によって判断するには少し複雑です。他に良い説明が考えられなかったので、現時点では諦めて性質として覚えてください。
32 平成28年度第1回(通算46回)問2

知識事項の確認
ここまで解いてきたのであれば、サービス問題に思えるでしょう。本番でもこのような問題が出ると良いですね。
(a) の検討
乾燥断熱減率は約1.0℃/100mです。よって、「誤」となります。
(b) の検討
湿潤断熱過程で保存されるのは相当温位です。よって、「誤」となります。
(c) の検討
湿潤断熱過程では相当温位は保存されます。よって、「誤」となります。
(d) の検討
空気塊が飽和するまでは、厳密に乾燥断熱過程です。よって、「誤」となります。
33 平成28年度第1回(通算46回)問3

知識事項の確認
これもサービス問題です。きちんと基本的な公式を覚えていれば正解できます。
(a) の検討
熱力学の第一法則では、空気塊に加えられる熱量は、空気塊のする仕事と空気塊の内部エネルギーの増加量の和に等しい、でしたね。よって、「$${Δu=ΔQ-ΔW}$$」となります。
(b) の検討
内部エネルギーの増加量は、温度変化と定圧比熱の積です。外部に仕事をすることなく、自分自身のエネルギーのみを蓄えるイメージですね。よって、「$${Δu=C_VΔT}$$」が正解です。
(c) の検討
重力加速度が出てくるのは、質量保存の法則ではなく「静力学平衡の式」です。
34 平成27年度第2回(通算45回)問2

知識事項の確認
エマグラム上で降水過程を考えることに慣れていれば、難しい問題ではありません。実技で問われることもある分野なので、きちんと理解してください。
(a) の検討
持ち上げ凝結高度を求める方法についてです。これは考えて解く問題ではありません。正解は「乾燥断熱線」となります。
(b) の検討
(a)の乾燥断熱線と、持ち上げ凝結高度で交わるのは等飽和混合比線で、この線は地上の高度では「露点温度」となります。これも考えて解答するものではありません。
(c) の検討
さきほど触れましたが、「等飽和混合比線」です。
(d) の検討
持ち上げ凝結高度を表す点を通る「湿潤断熱線」が、状態曲線と交わる点が自由対流高度を表します。
本問で扱うエマグラム上の各種物理量の変化は、実技試験でも頻出であるので確実に理解してください。過去には、実技で乾燥断熱線という名称を問う問題もありました。図ごと覚えるようにしてください。
35 平成27年度第2回(通算45回)問3

解法の確認
そろそろ、この図を見たらラッキーだと思えるようになったと思います。
この問題では、西側山麓から凝結が始まるまでの高度が不明です。しかし、山頂の東側は全て乾燥断熱過程であるため、結局西側山麓から凝結するまでに起きる温度変化は東側と厳密に正負が逆なので、打ち消されます。つまり、この部分はないものとして計算可能です。
それでは東側山麓の気温を計算します。
$$
25.0-0.5\times10 + 1.0\times15 =35.0[℃]
$$
よって、「④」が正解です。
36 平成27年度第1回(通算44回)問2

知識事項の確認
散々似たような問題を解いてきたと思います。記憶の定着のためだと思って解きましょう。
(a) の検討
水蒸気密度は、高度が上昇するにつれ値が小さくなります。一方で混合比は乾燥断熱過程であれば保存します。よって、「誤」となります。
(b) の検討
空気塊が下降する際は、外から仕事を受けるので内部エネルギーは上昇し、気温が上昇します。よって、「正」となります。
(c) の検討
設問の通り、空気塊内部に含まれる水蒸気はエネルギー(潜熱)を有しています。凝結するときに、このエネルギーが周囲に放出されるのです。よって、「正」となります。
37 平成27年度第1回(通算44回)問3

解法の確認
基本的な知識を正しく理解しているかを問う良い問題です。既に理解している知識で解けるはずなので、もし解けなかった場合は、抜けをなくすようにしてください。
(a) の検討
密閉した容器内の蒸気圧は飽和蒸気圧に他なりません。また、飽和蒸気圧は温度によってのみ決まる値です。したがって、蒸気圧は温度の順番と一致します。よって、「正」となります。
(b) の検討
冷静に考えましょう。容器内は飽和しています。つまり、すでに露点温度です。よって、「誤」となります。
(c) の検討
混合比に関する問題であれば、難しいことを考えずに公式を使いましょう。
$$
w=0.622\dfrac{e}{p}[kg/kg]
$$
(e:水蒸気圧 p:大気圧)
上記公式に、水蒸気圧(飽和水蒸気圧ですね)と容器内の気圧を順に代入すれば、「誤」であることが分かります。
38 平成26年度第2回(通算43回)問2

解法の確認
一見すると込み入っているようですが、単純に与えられた公式に代入して値を求めるだけの問題です。
(a) の検討
与えられた公式に代入すると、
$$
g\dfrac{T-\bar{T}}{\bar{T}}=10\dfrac{296-290}{290}=0.207 [m/s^2]
$$
よって、「0.2」が正解です。
(b) の検討
飽和する前の空気塊は、乾燥断熱減率によって変化しますので、「乾燥」が正解です。
(c) の検討
これはもう覚えたと思います。乾燥断熱減率は10℃/kmです。よって、「10」が正解です。
(d) の検討
空気塊と周囲の大気の気温減率の差から、1kmあたり7℃の割合で空気塊と周囲の大気の温度差が縮まります。今、6℃の差があるので、$${6/7=0.857=0.9℃}$$となり、「0.9」が正解となります。
39 平成26年度第2回(通算43回)問3
解法の確認
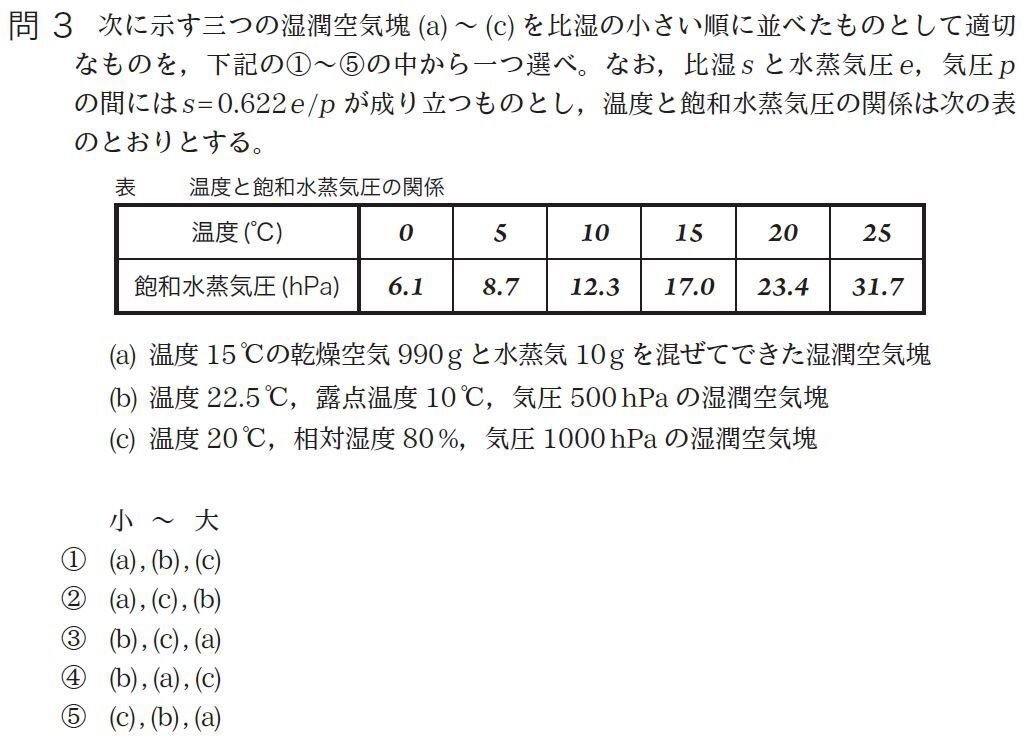
単純に与えられた比湿の式に値を代入し、比較するだけの問題です。
(a) の検討
対象の湿潤空気は1000gで、水蒸気の量は10gです。計算するまでもなく、比湿は10[g/kg]となります。問題は、10gの水蒸気を飽和せずに抱えることができるかですが、この点は大丈夫です。理由は、後ほど分かります。
つまり、最大でも10[g/kg]となります。
(b) の検討
気温22.5℃の飽和蒸気圧が与えられていないので、少なく見積もって20℃の飽和蒸気圧で計算します。
$$
w=0.622\dfrac{23.4\times10^2}{500\times10^2}=0.0291[kg/kg]=29.1[g/kg]
$$
少なくとも29.1[g/kg]であるということです。
(c) の検討
同じように計算しましょう。
$$
w=0.622\dfrac{23.4\times10^2\times0.8}{1000\times10^2}=0.0116[kg/kg]=11.6[g/kg]
$$
つまり、11.6[g/kg]となります。
以上の結果より、正解は「②」となります。
40 平成26年度第1回(通算42回)問2

知識事項の確認
しっかりと理解していれば瞬時に解ける問題です。もし解けなかった場合は、お手元の参考書を読み直してください。
(a) の検討
乾燥断熱過程であれば、混合比は保存します。よって、「〇」が正解です。
(b) の検討
既に飽和しているので、相対湿度は100%で変化しません。よって、「〇」となります。
(c) の検討
乾燥断熱過程であれば、水蒸気のエネルギーは放出されないので温位は保存されます。よって、「〇」が正解です。
(d) の検討
乾燥断熱過程、湿潤断熱過程ともに相当温位は保存します。よって、「〇」となります。
41 平成26年度第1回(通算42回)問3

解法の確認
与えられた式を変形し、密度を求めてみましょう。なお、1000hPaでの密度の比較なので、1000hPaでの温度、つまり温位を用いることを忘れないようにしましょう。
$$
ρ=\dfrac{m}{V}=\dfrac{PM}{RT}
$$
気体Aの密度
$$
ρ_A=\dfrac{m}{V}=\dfrac{1000\times10^2\times32}{R\times310}=\dfrac{10323}{R}
$$
気体Bの密度
$$
ρ_B=\dfrac{m}{V}=\dfrac{1000\times10^2\times32}{R\times300}=\dfrac{10667}{R}
$$
気体Cの密度
$$
ρ_C=\dfrac{m}{V}=\dfrac{1000\times10^2\times28}{R\times310}=\dfrac{9032}{R}
$$
気体Dの密度
$$
ρ_D=\dfrac{m}{V}=\dfrac{1000\times10^2\times28}{R\times300}=\dfrac{9333}{R}
$$
以上より、「④」が正解です。
本解説で使用した問題の著作権は一般財団法人気象業務支援センターに帰属します。本問題に対する解説は同センターから許可を受けた上で作成した筆者独自のものであり、同センターのものではありませんのでご了承ください。
また、本解説は筆者個人の理解に基づいて制作したものであり、その科学的妥当性を保証されたものではないことをご了承ください。
