「情報システム」分野の問題

大場みち子（公立はこだて未来大学）

　連載「教科『情報』の入学試験問題って？」第11弾です．前回までの入試問題解説に関してはこちら（https://note.com/ipsj/m/m1ca81b5d1e66）をご覧ください．

　「情報Ⅰ」では「「情報通信ネットワークとデータの活用」の中で，「情報システムとデータの管理」として情報システムについての理解が求められています．

　今回は，大学入試センターの「情報関連基礎」から「2013年度　第2問　旅行代理店の業務改善」を取り上げます．

　この問題は，旅行代理店が業務の作業手順を明確にして，仕事がスムーズに進むように業務を改善することを目的にしています．表1の作業一覧を元に業務フローを記述し，業務フローを元に，業務の進捗状況を電子的に記録する「業務記録システム」を考えます．この「業務記録システム」での業務の進捗状況がどのようになっているのかを問う問題です．

問1

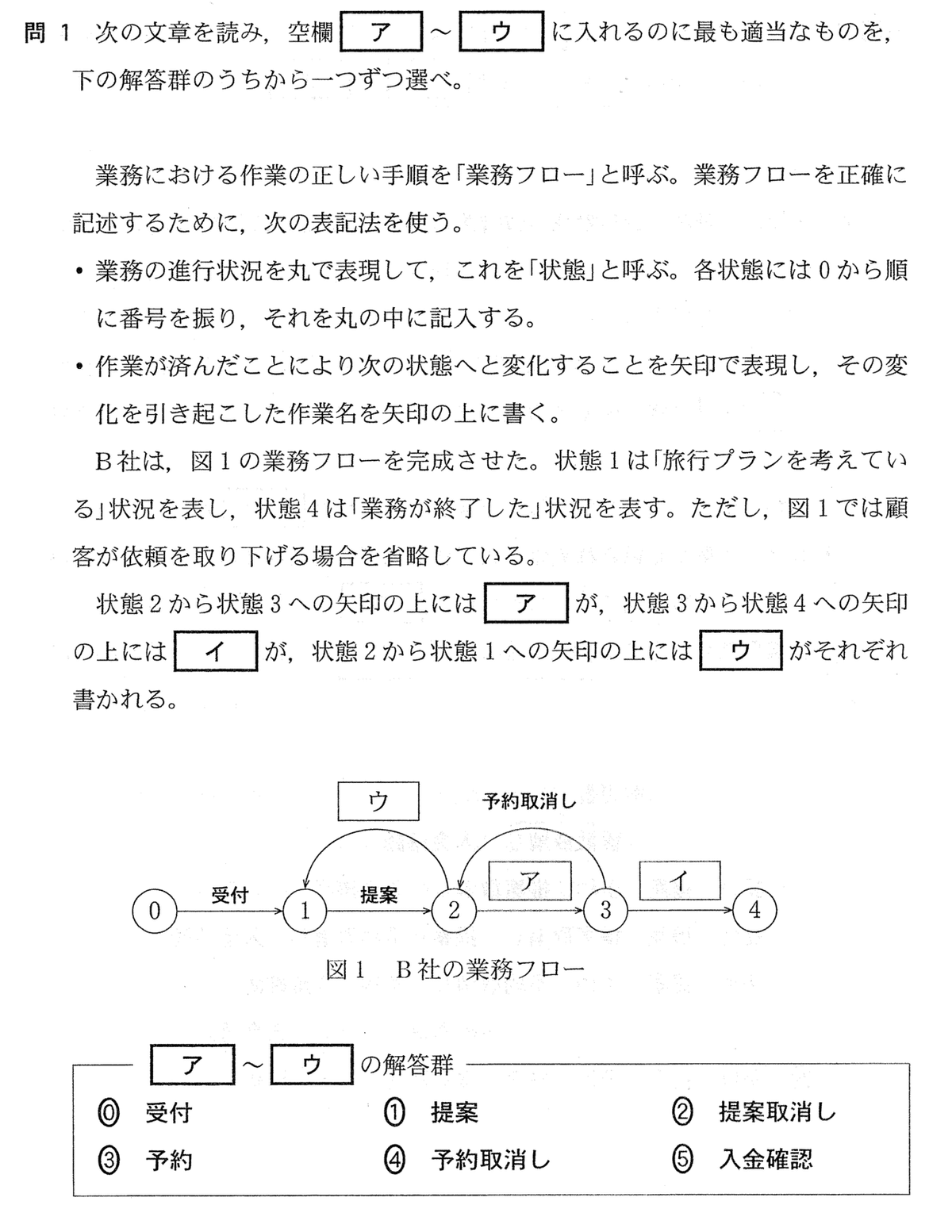
　ここでは，図1のB社の業務フローを完成することが目的になります．まず，「業務フロー」の定義と表記方法の説明が書かれています．図1の業務フローは状態遷移図を使って書かれています．

　図1の（ア）〜（ウ）は表1をもとに考えるわけですが，ポイントは直線の矢印と戻る矢印の2種類の作業があることです．直線の矢印の作業は受付　提案，戻る矢印の作業は予約取消しです．これらの情報から，予約取消しは（ア）の作業を取り消すことが想像できるので，③「予約」となります．（イ）は最後の作業なので，⑤「入金確認」となります．（ウ）は予約と予約取消しの関係と同じですから，提案に対して②「提案取消し」となります．

　別の考え方を説明します．表1の作業の内容から受付　提案　予約　入金と提案取消し　予約取消しでは作業の性質が異なることが分かります．図1では前者の作業が普通の作業（正常処理）で「→」で表され，後者の作業は取消しの作業（例外処理）で「↶」で表されているという区別ができます．このように考えると，（ア）は③「予約」，（イ）は⑤「入金確認」，（ウ）は②「提案取消し」という解答が容易に分かるでしょう．

解答
（ア）③「予約」，（イ）⑤「入金確認」，（ウ）②「提案取消し」

問2

　ここでは業務フローに従って「受付」から「入金確認」までの作業が終了した記録の作業列を記録したものを「終了作業列」と定義しています．

　（エ）は終了作業列の例を問う問題です．ここでは，図1の流れにそったものが選ばれなければいけません．図1の流れにそって，1つずつ確認していけば（エ）の解答は「③」ということが分かりますが，つぎのように考えてみましょう．

　ここでのポイントは，「入金確認」まで終了するには，つぎの2つのケースになります．

（1） 例外処理がまったくない終了作業列
具体的には，受付　提案　予約　入金確認 という系列です．

（2） 例外処理がある場合，受付で始まり，例外処理の前後に例外処理に対する正常処理が実施され，最後に入金確認で終了する終了作業列
具体的にはつぎの条件を満たす必要があります．
（i） 受付で始まり，入金確認で終わる
（ii） 受付　提案　予約　入金確認 という順序で出現する
（iii） 取消しが発生する場合，提案　提案取消し，または，予約　予約取消しが含まれる

　（1）は選択肢にないので，（2）に該当し，具体的な条件を満たす③が（エ）の解答になります．

（オ）は図1を見ると分かる通り，予約取消しが発生すると入金確認まで行くには，必ず予約をしないと次に行かないので，「1」になります．

　8個の作業が記録される終了作業列で提案が2つ含まれている場合はつぎの2通りです．

A: 受付　提案　提案取消し　提案　予約　予約取消し　予約　入金確認
B: 受付　提案　提案取消し　提案　提案取消し　提案　予約　入金確認

　上記より，提案と提案の間にはAは1個（提案取消し），Bは3個（提案取消し　提案　提案取消し）の作業が含まれているので，（カ），（キ）は「1」「3」（順不同）となります．

　終了作業系列で例外がまったくない終了作業系列は上記（1）の4個の作業です．この終了作業系列に，提案取消しと予約取消しの例外作業が発生すると，上記（2）のように，例外作業のつぎに，必ず，それぞれの正常作業の提案または予約が追加されるので各2つずつ作業が追加されることになります．つまり，提案取消しと予約取消しの合計がn個の場合，2✕n個の作業が追加になります．

　以上より，（ク）「2」✕n＋（ケ）「4」が解答となります．

解答
（エ）③，（オ）「1」，（カ）（キ）「1」「3」（順不同）
（ク）「2」（ケ）「4」

問3

　提案取消しと予約取消しが0個の場合の終了作業列は問2の（1）の場合のみなので，（コ）「1」となります．

　提案取消しと予約取消しが合計5個のときの場合分けを考えます．これは，すべての場合を書き出すのが一番簡単でしょう．提案取消しが5個の場合，予約取消しは0個となり，提案取消しが4個の場合，予約取消しは1個となります．これを繰り返すとつぎの表-1のようになるので，解答は（サ）「6」通りとなります．

表-1　提案取消しと予約取消しが合計5個のときの場合分け

　つぎに，上記の表の項番1〜6のそれぞれに対して，終了作業列が何通りあるかを考えます．基本的に，提案取消しと予約取消しの数が逆転している項番1と6，項番2と5，項番3と4の場合の数は同じになります．これは，提案取消しと予約取消しは順序が違うだけで，場合分けとしては同等だからです．

　単純化のために図1の業務フローの作業名を
受付：a，提案：b，提案取消し：b’，予約：c，予約取消し：c’，入金確認：dとします．

　まず，項番2の提案取消しが4個で，予約取消しが1個の場合を考えてみます．簡単なので，すべて書き出してみましょう．

a，b，b’，b，b’， b，b’，b，b’，c，c’，c，d
a，b，b’，b，b’， b，b’，c，c’，b，b’，c，d
a，b，b’，b，b’， c，c’，b，b’，b，b’，c，d
a，b，b’，c，c’， b，b’，b，b’，b，b’，c，d
a，b，c，c’，b’， b，b’，b，b’，b，b’，c，d

　以上より，（シ）「5」通りとなります．

　これは，同じものがあるときの順列と考えることもできます．n個のうち，同じものp個，q個，r個が同じであるとき，これらn個を1列に並べる順列の総数は次のようになります．

n!／p!q!r!　(p+q+r＝n)

　ここでは，上記のすべての書き出しを見れば分かりますが，b’とc’だけに注目すれば問題ありません．同じものb’が4個，c’が1個なので，つぎのような解答になります．

(4＋1)！／4！1！＝5（通り）

　一方，提案取消しが1個，予約取消しが4個の場合もつぎのようにpとqの数が入れ替わっただけなので，同様の総数5通りになります．

(1＋4)！／1！4！＝5（通り）

　これは，5個の中から4個を選ぶ組合せと考えることもできます．

　問題文に書かれていますが，提案取消しが3個，予約取消しが2個の場合を上記と同様に考えてみましょう．この場合は，次のようになるので，総数は10通りです．

(3＋2)！／3！2！＝10（通り）

　提案取消しが2個，予約取消しが3個の場合も10通りになります．これで，問題文の内容と一致することが分かりましたね．

　以上をまとめると，表-2のようになるので，提案取消しと予約取消しが合計5個の場合の終了作業系列の総数は32通りで，解答は（ス）3（セ）2となります．

表-2　提案取消しと予約取消しが合計5個のときの終了作業系列の総数

　同様に，提案取消しと予約取消しが合計4個，3個，2個，1個の場合を計算すると，表-3のようになります．したがって，作成する表は63通りとなり，問題文の内容と一致することが分かります．

表-3　提案取消しと予約取消しが合計4個，3個，2個，1個のときの
終了作業系列の総数

解答
（コ）「1」，（サ）「6」，（シ）「5」，（ス）「3」，（セ）「2」

■大場みち子（正会員）
　公立はこだて未来大学教授．情報処理学会フェロー，総務理事・事業理事を歴任，IPSJMooc（https://sites.google.com/view/ipsjmooc/）第4章の「情報システム」を担当．

情報処理学会ジュニア会員へのお誘い

小中高校生，高専生本科～専攻科1年，大学学部1～3年生の皆さんは，情報処理学会に無料で入会できます．会員になると有料記事の閲覧，情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります．ぜひ，入会をご検討ください．入会はこちらから！