岐阜県立多治見看護専門学校 過去問(令和5年度一般入試) 数学 解答解説

こちらの岐阜県立多治見看護専門学校 過去問の解答解説は、同校を受験する受験生のためにアイプラスアカデミーが作成したものです。

岐阜県立多治見看護専門学校の一般入試を受験するみなさんの直前対策にご活用ください！

なお、同じく令和5年度一般入試の英語の解答解説についても公開しています！

看護予備校アイプラスアカデミー＜社会人専門＞

岐阜県立多治見看護専門学校 過去問(令和5年度一般入試) 数学の注意点

数学については、以下のように必答問題と選択問題があります。

第1問，第2問，第3問は必答問題。
第4問，第5問，第6問から2問を選択。

岐阜県立多治見看護専門学校 過去問(令和5年度一般入試) 数学 解答解説

第1問(必答問題)

(1)

解答：$${7+4\sqrt3}$$
解説：$${a^2+b^2+2ab=(a+b)^2}$$であることから、$${a+b}$$の値を考えればよいことがわかる。
$${a}$$と$${b}$$はそれぞれ$${2+\sqrt3}$$の整数部分と小数部分なので、$${a+b=2+\sqrt3}$$である。
よって、$${(a+b)^2=(2+\sqrt3)^2=7+4\sqrt3}$$

(2)

解答：$${a=1,b=2}$$
解説：$${\sqrt{2}a+\sqrt{3}b=\sqrt2+2\sqrt3}$$より
$${(a-1)\sqrt{2}+(b-2)\sqrt{3}=0}$$
$${a-1=0,b-2=0}$$
よって、$${a=1,b=2}$$

(3)

解答：$${m<4}$$
解説：$${y=x^2-(m+4)x+m-4}$$のグラフは下に凸であるので、この方程式の解（$${y=0}$$のときの$${x}$$の値）が正と負になるには、
$${x=0}$$のときの$${y}$$の値が0より小さく（$${x}$$軸よりも下）になればよい。

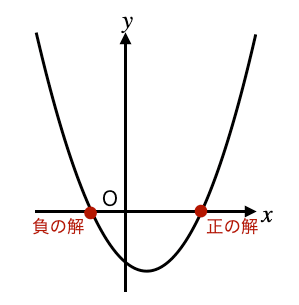
よって、$${x^2-(m+4)x+m-4}$$に$${x=0}$$を代入すると
$${m-4}$$となるので、これが0より小さくなることから
$${m-4<0}$$
$${m<4}$$