【ラビットチャレンジ】機械学習レポート
◆機械学習について、人がプログラムするのは認識の仕方ではなく、学習の仕方である。
◆Section1:線形回帰モデル
【要点のまとめ】
ある入力から出力を予測する
直線で予測→線形回帰
曲線で予測→非線形回帰
教師あり学習
慣例として予測値には<ハット>をつける
x→線形回帰モデル→y ^
説明変数が1次元の場合→単回帰モデル、直線
説明変数が多次元の場合→重回帰モデル、曲面
パラメータは最小二乗法※で推定
※学習データの平均二乗誤差を最小とするパラメータを探索
【参考図書・関連情報】
○例
・駅の平均乗降客数と売上高の関係
・店の売上と来客数
→このシンプルな式に季節や天気などの変数が追加されるイメージ
↓参考サイト
https://www.statweb.jp/method/kaiki-bunseki/senkeikaiki-case
【実装演習】
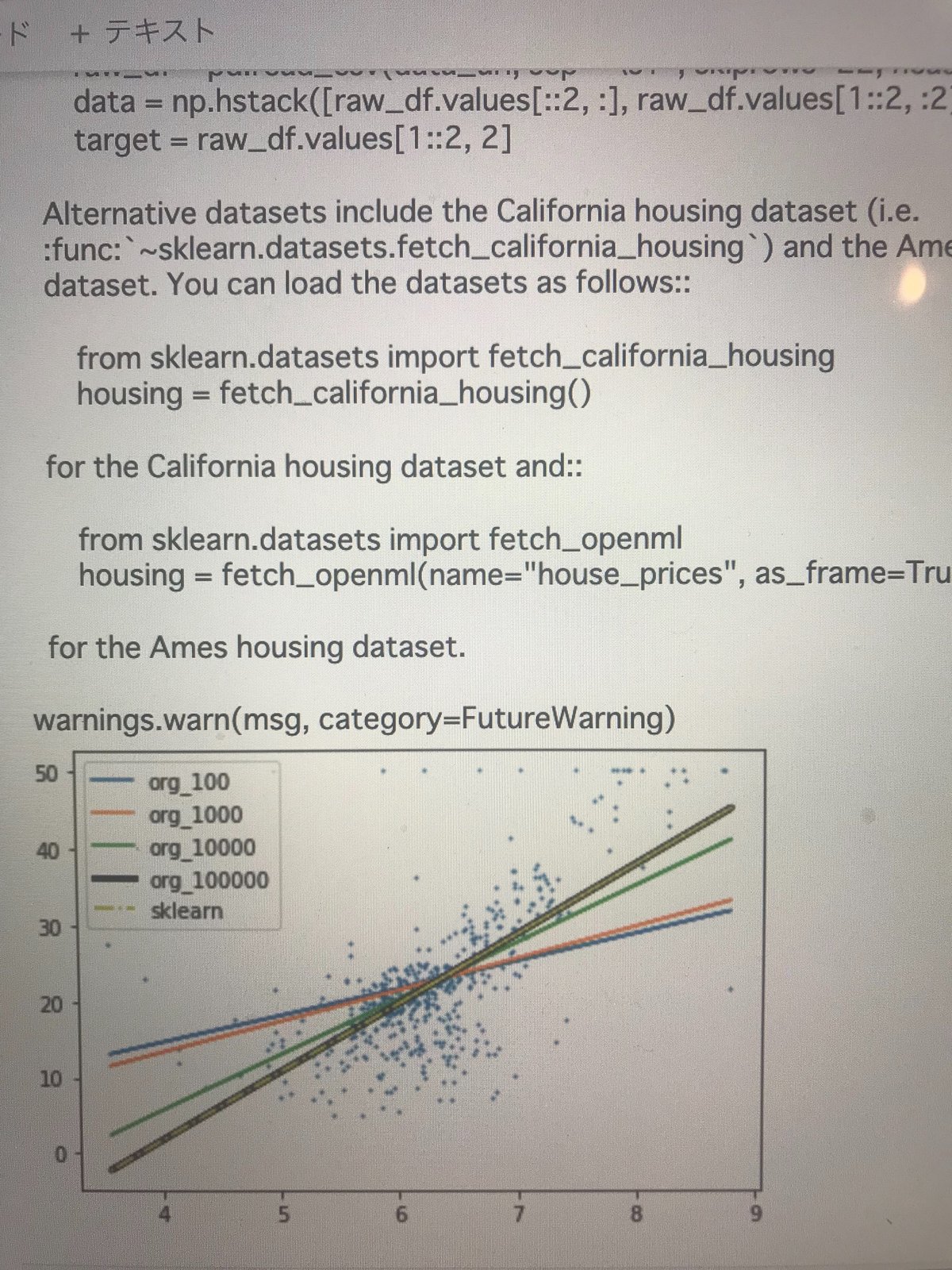
参考サイトを確認しながら
ボストン住宅情報で実装(グラフで可視化)
ーーー
for i in range(100000):
# 予測値y_hatを計算する。
y_hat = np.dot(large_x, w)
# 損失関数の微分を計算する
dw = np.dot((y - y_hat), large_x) / len(large_x)
w += alpha * dw
ーーー
↓参考サイト
https://recruit.cct-inc.co.jp/tecblog/machine-learning/linear-reg/
◆Section2:非線形回帰モデル
【要点のまとめ】
○未知パラメータは線形回帰モデルと同様に最小二乗法や最尤法※により推定※最尤法とは、与えられた標本から、それらが得られる確率を最大化する確率分布を推定する手法
○学習データに対して、十分小さな誤差が得られないモデル→未学習モデルの表現力が低いため、表現力の高いモデルを利用して対策する○小さな誤差は得られたが、テスト集合誤差との差が大きいモデル→過学習
<対策>
・学習データの数を増やす
・不要な基底関数(変数)を削除して表現力を抑止(特徴量選択)
・正規化法※を利用して表現力を抑止
【参考図書・関連情報】
y=f(X,β)+ϵ
線形パラメータとの関係を適切にモデル化できない場合、通常の線形回帰ではなく非線形回帰を使用します。
【実装演習】
参考サイトでコードを確認
ーーー
x1=np.arange(16)
fit = np.polyfit(x1,y,5)
y2 = np.poly1d(fit)(x1)
ーーー
↓参考サイト
https://kgrneer.com/python-numpy-scikit-kaiki/
◆Section3:ロジスティック回帰モデル
【要点のまとめ】
○ロジスティック回帰モデル
分類問題を解くための教師あり機械学習モデル(教師データから学習)
入力とm次元パラメータの線形結合をシグモイド関数に入力
○シグモイド関数
入力は実数
出力は必ず0~1の値
○尤度関数
尤度関数を最大化するようなパラメータを選ぶ推定方法を最尤推定という
○確率的勾配降下法(SGD)
データを一つずつランダムに(「確率的」に)選んでパラメータを更新
【参考図書・関連情報】
性能評価指標
・混同行列(confusion matrix)
・正解率(accuracy)
・適合率(precision)
・再現率(recall)
・F1スコア(F1-score)
・AUC(曲線下面積)
【実装演習】

from sklearn.linear_model import LogisticRegression
を使用
◆Section4:主成分分析
【要点のまとめ】
多変量データの持つ構造をより少数個の指標に圧縮
少数変数を利用した分析や可視化(2・3次元の場合)が実現可能
【参考図書・関連情報】
実務上では
累積寄与率が、70~80%に達するところまでの主成分数を採用することが多い
https://www.macromill.com/service/data_analysis/principal-component-analysis.html
【実装演習】
試験問題を解くために作成したアウトプット
データが少ないので綺麗な形とはならない

◆Section5:サポートベクターマシン
【要点のまとめ】
SVM (support vector machine)と略される。
sign関数を使用し、引数が正の場合には+1、負の場合には1を返す。
決定関数f(x)の正負で特徴ベクトルxのクラスを識別。
分類境界を挟んで2つのクラスがどのくらい離れているかをマージン(margin)と呼び、マージン最大化を図る。
分類境界に最も近いデータ点をサポートベクトルと呼ぶ。
【参考図書・関連情報】
○カーネル法
データを変換することで、非線形構造を線形構造に変換し、
線形データ解析手法で非線形データを容易に?扱うことができる。
カーネル関数を使用することからカーネル法と呼ばれる。
カーネル関数のカーネルとは・・・
↓参考サイト
https://hkawabata.github.io/technical-note/note/ML/svm.html
【実装演習】
参考サイトでコードを確認

この記事が気に入ったらサポートをしてみませんか?
