【今こそ素数さんを知る!❺】
阪大でちょっとした有名人の素数さん。
でも素数さんとはいったい何者なのか?
世界で一番詳しい素数さん記事をお届けします。
第1回はこちら
【今こそ素数さんを知る】第⑤回
あなたも10秒で素数の無限性を証明できる!
整数論にばゼータ関数という、めっちゃ重要な関数があるんですよ。
整数論とはゼータ関数を研究することだと言っても過言ではないくらい、偉い関数なんです。
ゼータは素数が集まってできたもので、そいつのことを調べると逆に素数のことが分かります。
数式が出てきますが、文系の人でも簡単に理解できるくらい簡単なので、少しだけ我慢してください(笑)。
一番単純なゼータ関数は、オイラーとリーマンが発見したこんな関数です(掛け算バージョン)。
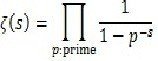
Π(パイ)という、難しそうな記号がありますよね。
でも∑(シグマ)って最初に見た時は難しそうだけど、結局単なる足し算でしたよね。
数学って習ってみたら意外と簡単で、 Πも難しそうに見えるけど、シグマが足し算だったら、こっちは掛け算です。
pは素数のことで、pの部分に2,3,5,7,11,13...と、素数が存在する限り代入したものをかけ合わせていきます。
ゼータは素数を集めてできているので、素数の情報を持っています。
さらに、ゼータ関数は次の形でも計算できます(足し算バージョン)。

ゼータに1を代入してみましょう(s=1)。 足し算バージョンからは、1+1/2+1/3+・・・となり、これは無限大になることが証明 されています。
一方掛け算バージョンを使うと、もし素数が有限個しかなかったら有限個の分数を掛けたことになります。
数を有限個掛けたら、結果も当然有限。
でも足し算バージョンの結果 ζ(1)が無限になることがわかっています。
ということは、素数は無限個ないとおかしいですよね?
なんとこれで、素数が無限個あることを証明できました!
これはオイラーによる証明です。
どうですか、ゼータのすごさが見えてきませんか?
ζ(1)の値の中に、素数が無限個あるという情報が詰まっているんですよ!
そうすると、ゼータに他の値を代入してみたり関数のことを調べてみれば、素数についてもっとレベルの高いことが分かるかもしれないと思いませんか?
実際、それは正しいんですよ。
実はこのゼータ関数に関して一番難しい予想がリーマン予想というもので、100万ドルの懸賞金がかかっています。
よく数学史上最難問とも言われますが、ゼータ関数についてわかっていないことが沢山あります。
しかも、今となっては無限種類のゼータがいて、多様なゼータが研究されています。別物だと思っていたゼータ同士が結びついたり、ゼータは魅力的なことをいっぱい知ってい ます。
数学は知れば知るほど面白くなります。
最初は整数のことを知りたいから、そのために素数のことを調べてみた。
そしたら、素数のことを知るにはゼー タのことを理解すればいいとわかったんです。
ですので整数論の研究者は躍起になってゼータのことを研究しています。
そして僕の研究内容もゼータなんです。
