
【WebGL】CG入門: front or back facing triangles の見分け方
WebGL Fundamentals の写経を行っていく.
この3Dの説明で,back と front facing triangles の culling (= not drawing)の設定が出てくるが,どうやって見分けるんだと疑問になったのでここにメモしておく.

Front / Back facing triangles の定義.
CCWがFront facingで,CWがBack facing と定義される.
https://webglfundamentals.org/webgl/lessons/webgl-3d-orthographic.html
以下のページも参考になる:

https://learnopengl.com/Advanced-OpenGL/Face-culling
同じ図形でも回転させて,裏側に行ったら見えなくなるようにできる.
これが,front と back facing triangles を定義する意義だ.
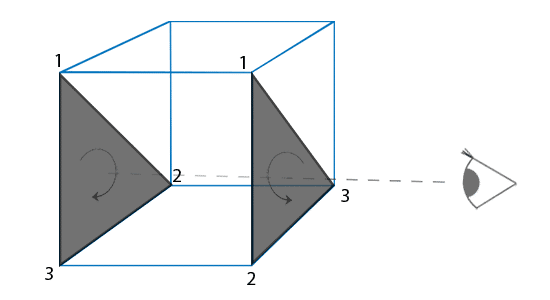
The camera direction's important to decide the direction.
結局カメラの向きがどこ向いているのか,についての説明が,webGL Fundamental のページには省略されていたのが混乱の原因であった.
三角形の3つの頂点の座標から,どうやって見分ける?
CG の Rendering では,三角形 を組み合わせて,描画される.
三角形の座標からどうやって見分けようか.
あわよくば,高速で見分ける条件式みたいなの得られんかな.
三角形を眺めた時に,三角形の頂点(Vertex)で作られるベクトルの外積ベクトルを考える:
$$
\vec{E} = (\vec{v}_{2} - \vec{v}_{1}) \times (\vec{v}_{3} - \vec{v}_{1})
$$
このベクトルと,カメラの向いている向きベクトルの内積が大事になってくる.
Default のカメラ視点が向いている向きを $${\vec{D} = (0,0,-1)}$$ としておく.
$$
C = \vec{E} \cdot \vec{D} = - E^z
$$
各頂点 $${i = 1, 2, 3}$$の位置ベクトルを,$${\vec{v}_i = (v^x_i, v^y_i, v^z_i)}$$のように書いておく.
さらに,簡単のために,$${\vec{w}_{ij} = \vec{v}_i - \vec{v}_j }$$ としておく.
$$
C = - (w_{21}^x w_{31}^y - w_{21}^y w_{31}^x)
$$
これより,得たかった条件式は,
Back facing face if $${C > 0}$$
Front facing face if $${C < 0}$$
となる.
例題
WebGL Fundamentals のページによると,以下のようになるらしい:
Backward?
0, 0, 0,
40, 50, 60,
700, 800, 900,
Frontward?
0, 0, 0,
700, 800, 900,
40, 50, 60,
になると言う.証明してみる.
Backward? の方は,
$$
C = - (40 \times 800 - 50 \times 700) = +3000 > 0
$$
Fackward?の方は,
$$
C = - (700 \times 50 - 800 \times 40) = -3000 < 0
$$
確かに,そうなっていた.
何かの役にたてばと,共有しておきます.
