
【数学】コラッツ予想との不定期日記(1)
なんかふと,コラッツ予想(Collatz conjecture)のことを,色々考えてしまうので,ここにその記録を報告しておこうと思う.
これは恋ですね.
コラッツ予想が証明できないだけのノートです.
まあやってみて,そのヤバさを感じて欲しいです.
何がやばいかっていうと,カオスっぽい感じなんじゃ?
コラッツ予想:Collatz conjecture


$${T^{k}(n) = 1}$$ となる有限な$${k}$$があることを示せるかが,コラッツ予想です.
いきなりコラッツ予想やるの,いろんな人たちのプレイを見て,無理ゲーっぽい感じだったんで,まずは自称弱いコラッツ予想を作りました.("弱い"でいいんかな?厳密な表現は知らない.)
弱いコラッツ予想
自称弱いコラッツ予想はヒントになるかもと思って作りました.やるまでもなさそうなのですけれど.


このマップの下で,$${U^{k}(n) = 1}$$ となる$${k \in \mathBb{N}}$$があるかどうかかどうかが,今回の予想です.
ぶっちゃっけ,この予想は数学的帰納法を使っちゃえば簡単っぽいので,証明するまでもなく自明っぽい感じなんですけどね.(ガチの人に,数学で,っぽい使うな,ってキレられそうですね.すみません)
一応,数学的帰納法でやると,$${n = 1}$$は自明で,$${n = l}$$ まで,すでに証明できたとして,$${n = l + 1}$$ を試すと,偶数も奇数でも,マップの写った先がいずれ $$n < l + 1$$ になるので,証明できたことになるでしょう.数学苦手なので,ちゃんと記述できません.許してください.
コラッツ予想の1つのヤバさは,$${n = l + 1}$$ を試すと,いつになっても,$${n > l + 1}$$になり続ける場合が現れることですね.
直感的証明の準備:2進数表現を使うよ
これは好みの問題なんですけどね.
直感的にホントにそうなるかがわかるような証明方法が好きなんです.
数式にあまり頼らないで,証明してみたいなと.
可視化するのに,2進数を使います.

これを使うと,コラッツマップの軌道はこんな感じ.
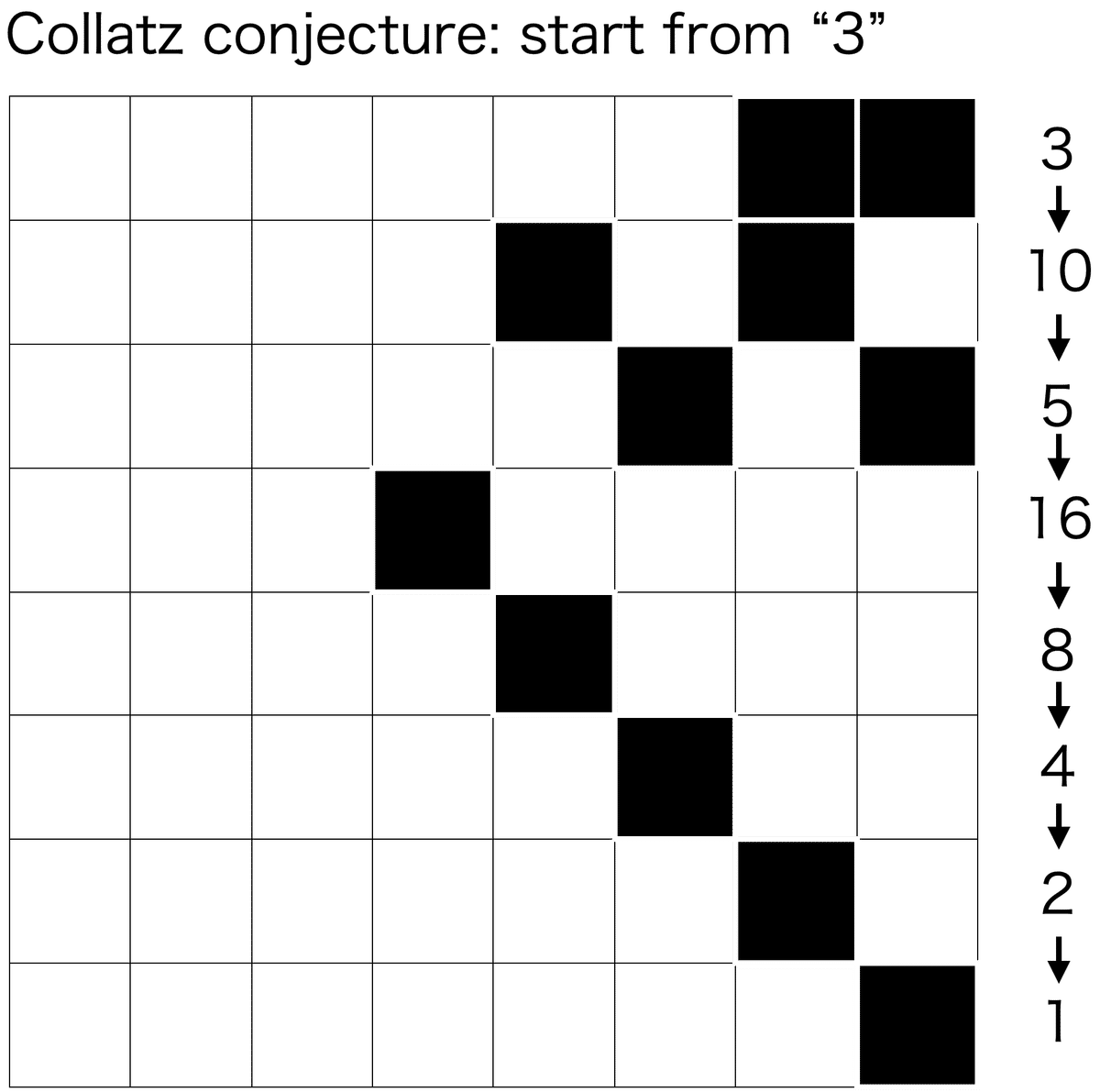
これみてわかるのは,変換していくうちに,たった"1つ"のビットだけ,■が残れば,証明終わり,勝ちってことですね.
任意の自然数は,2の冪乗で展開できるから,
ある奇数(odd)は,$${n = 2^{0} + \sum_{l = 1}^{M} 2^{n_l}}$$ のような感じで表せますね.

この方法を使って弱いやつ(弱いコラッツ予想)を倒してみたいと思います.多分,倒せたと思ってます.
2進数可視化法での弱いコラッツ予想の証明
弱いコラッツマップを,オートマトンとして捉えて,以下の状態遷移図で表してみます:

step1 が n+1 の演算で, step2 が n/2 の演算.
このオートマトンに,以下のような,任意の奇数を突っ込みます:

■(1)のブロックと,□(0)のブロックに分けて考えています.
各ブロックは順に下の桁から,
■のブロック:$${I^{1}}$$個の1が並ぶ.
□のブロック:$${J^{1}}$$個の0が並ぶ.
■のブロック:$${I^{2}}$$個の1が並ぶ.
□のブロック:$${J^{2}}$$個の0が並ぶ.
...
とこんな感じで表しています.
そんで,これをさっきの弱いコラッツマップのオートマトンに入れると,
必ず,step1 からスタートして,以下のような挙動をしたのちに,いずれ,1になります.

これ,どの $${k}$$ で, $${U^{k}(n) = 1}$$ になるのかもわかるメリットがあります.
$$
k = 1 + \sum_{m = 1}^{M} \left[ (I^{m} + 1) + (J^{m} - 1) \right]
$$
(数え間違ってたら,すみません.)
さて,次はコラッツマップに挑んでみます.
コラッツ予想への挑戦

もう一度,3から始めた時の挙動を書いておくと.こんな感じです.
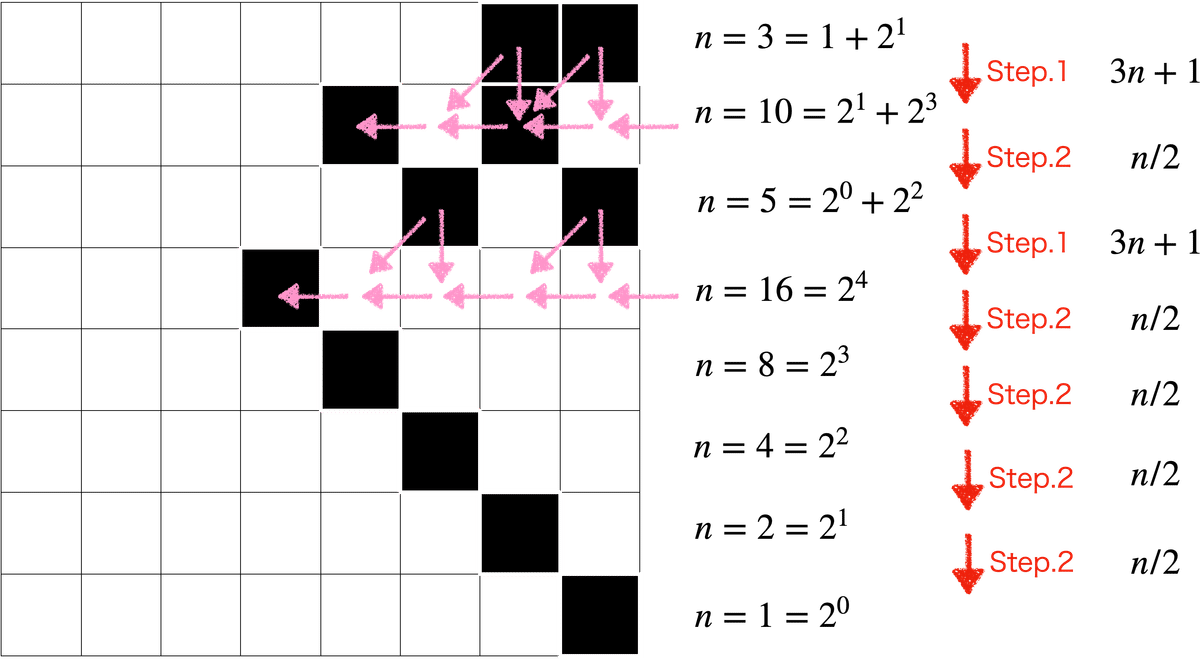
ピンクの矢印は,ビットの和演算と,繰り上げを示しています.
任意の奇数を3倍+1した時の各■ブロックの動きを見てみます.

繰り上げが起こってます.
この繰り上げが,他の■ブロックに届いたり,届かなかったり,届いた結果さらに繰り上げが起こって,その連鎖が起こったりと,色々と複雑な挙動をしそうなのが伝わってきます.
例えば,1を3倍し続けた時の挙動だけをみると, こんな感じです.
1=$${3^{0}}$$ から始めて,下段につれて,$${3^{1}}$$,$${3^{2}}$$,$${3^{3}}$$,...です.

■が出てくる規則があるっぽいけど,よくわからない.
大小異なる三角形の■の塊が不規則に出てきている感じが不思議ですね.
なんか,三角の■の塊がテントで,その周りで異世界人が住んでいて,わちゃわちゃと楽しそうです.
あ,わからなくて混乱してるだけです.
テレンス・タオ氏の論文をちらっとみました.
アブストラクトしか読んでないのですが,以下のことが証明できたというものです:
$${\lim_{N \to \infty} f(N) = +\infty}$$となる,
関数$${f: \mathbb{N} \to \mathbb{R}}$$で,
ほとんどの$${N \in \mathbb{N} }$$において,
$${ Col_{min}(N) \leq f(N) }$$を満たす.
そしてここでも出ましたね,三角形のテントたち.
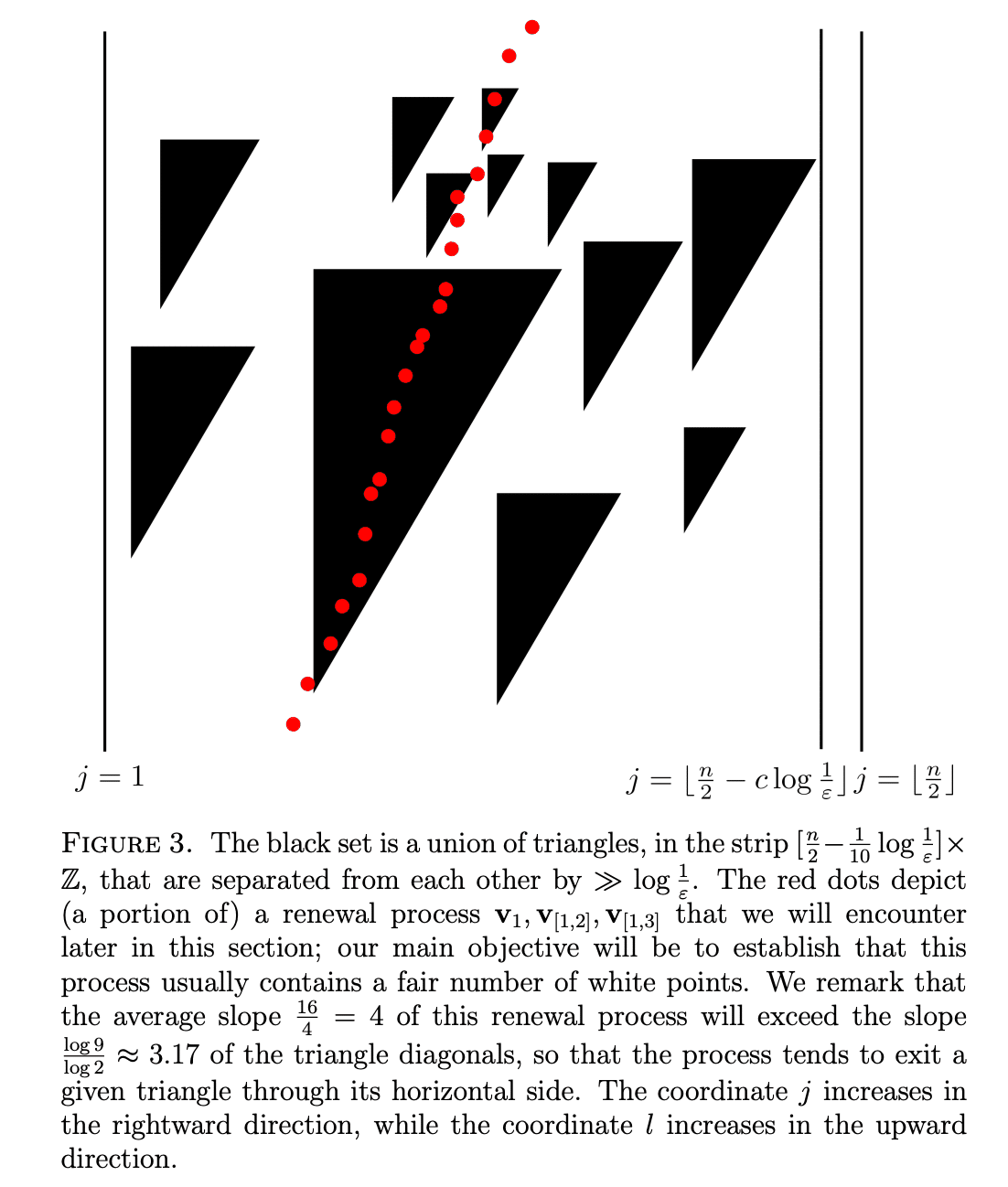
https://arxiv.org/abs/1909.03562
この論文での三角形の意味,自分のとは違っているとは思いますけどね.
3倍した結果,厄介な動きをしているのは確かな気がします.
なんかいい方法あるんかなぁ.
ヲタクに恋は難しい.
しかも,三角関係なんて無理じゃ.
