ひろゆきさんにはわからない、ちゃんと理解する為の位置エネルギー解説
但し書き
① 位置エネルギーについて一般の方にも理解してもらい、物理界隈の裾野を広げる
② 読者、視聴者の理解度に依らず、ちゃんとわかりたい人にわかってもらうために、数学の難解さによる心理的障壁を極力減らし、物理の基本法則にフォーカスして解説する。数学の厳密性は問わない。難易度的には物理好きの中学生~物理学部初年度向け
③ 一般向けの解説記事、動画を作成することで、自信の理解力の向上とプレゼン能力を向上させる。この記事は動画作成における草案のようなものである。草案であり、文章であるので、この記事に限っては読者の読みやすさはあまり考慮しない(どうしても長くなるので出来ない)。あまりにも暇で文が読みたくなった人にはおすすめするが、それなら教科書を読めば済む話である。文字媒体の最高傑作はプロが作った教科書であろう。
この記事の概要
著名人である西村博之氏が、「位置エネルギーは存在しない、虚構のものである」という旨の論を、youtube上で発信した。氏の発言力によって多くの人々が物理に関心を寄せたことは大変喜ばしいが、同時に多くの誤解が生じた。この記事はひろゆき氏を中心とした、物理を知らない人々の位置エネルギーへの誤解を解くものである。
ひろゆき氏の誤解の概要
細かい間違いは多少あるが、本旨の誤解は二つ
① 重力は宇宙空間では発生しない。位置エネルギーは重力によって生まれる。よって宇宙では位置エネルギーは存在しない
② 位置エネルギーは、虚数と同じような概念上作られたものであって、存在するのは重力だけである。よって重力だけで説明すればよい
この二つを解決したあとに、コメント欄、SNSなどで散見されたよくある誤解などについても解説していく
解説
キーワードは二つ。「重力」と「位置エネルギー」である。まず重力とはなにか?中学生の頃、「質量0.1kgに1Nの重力がかかる」という様に教わるのが最初だろうか。実はこれは「万有引力が地表面の物体に働く時のみ成立する関係である」。
では、万有引力とはなんだろうか?簡単に図で示してしまおう。
万有引力の大きさg(r)とすると、

万有引力は二つの物体が存在するだけで、その二物体に相互作用し引き合う力であり、
数式ではその大きさを

と表す。Gは万有引力特有の比例定数、万有引力定数≒6.67*10^-11m^3/kg*s^2である。
式をよく見てみる。二物体の重さの積Mmが分子にあり、距離の二乗が分母にある。つまり重ければ重いほど強く引き合い、離れれば離れる程弱くなる。定数には10^-11、つまり量全体を1000億分の1の大きさにする部分が含まれている。なので、人間程度の質量の二物体が近づいてもその力を感じることはできない。もっぱら星から感じる力である。
そしてはるか彼方にある星からは、遠すぎて力は微小量しか及ばない。
ところでg(r)の(r)とはどういう意味だろうか?これは万有引力をrの関数とみなす、という意味である。rの値が変化にともなってg(r)の値も変わるとき、g(r)はrの関数と言える。Gは定数であり、Mmもある二つの物体に着目すれば基本的には変わらない。(例外;星の爆発による質量減少)よって右側で変わるのはrの部分だけである。
ではそのrも固定したらどうなるか?
地球の半径Rは約6400kmである。地表からオゾン層までが30kmなので、地表にあるものと地球の重心との距離はだいたいRと置いてよいだろう

そうすると万有引力のすべての文字を定数で表すことができる。地球の質量は5.97*10^24kgなので、単位に気をつけてまとめれば
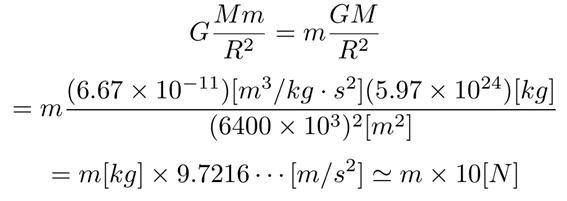
式を見れば、地球表面上にある物体に定数がかけられていることがわかるであろう。この定数を重力加速度gといい、大体10m/s^2なので、中学校では0,1kgの物体に1Nの力がかかると教えられる。高校ではmgの力がかかると習うだろうか。ひろゆき氏はそれをおぼろげに覚えていたのだろう。しかしこれまでの流れを見れば、地球表面から離れた物体に対して、rを地球の半径Rで考えて定数にまとめたgが通用しないのはあきらかである。宇宙にいって突然重力が0となるわけではない。ではなぜ力があるのに落ちてこないか?というのは状況(初期条件)によって様々な理由があり、ニュートンの運動方程式や円運動の話、座標系の話など話が多岐にわたり本旨から逸れるので、今回は割愛する
これだけでひろゆき氏の意見①の否定にはなるが、②の否定はできていない。というより、コメント欄やSNSを見ても圧倒的に誤解が多いのは位置エネルギーの方であった。そのような一般の曖昧な見方が「位置エネルギーは存在しない」というひろゆき氏の主張につながるのであろう。まず位置エネルギーの認識を明確にするために、基本概念を解説していく。
物理とは数学を言語としてこの世の理を解明する学問である。なぜ数学が必要なのか?それは数学言語が最も意思の齟齬を生じずに論理を説明できるからである。言語では、一つの言葉、文に多重の意味が込められてしまい、話し手聞き手によって多数の解釈が生じてしまう。しかし数式ならば等号で結ばれた左辺右辺の関係は必ず等しく一対一の対応を保つことができる。やはり、難しくても数学から始めるのが科学であろう。安心して欲しい。数式の意味は随時簡単に補足する。
位置エネルギーの定義
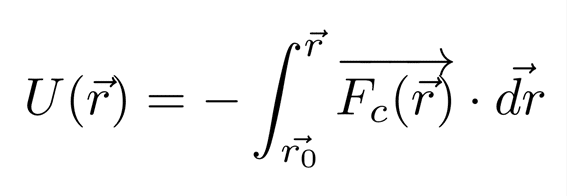
文字式は数字の置き換え、()は関数であることが、これまでの説明でも行ったが、文字の上に変な矢印がある。これは、「この文字の数字は大きさだけでなく、向きの情報も持ってますよ」という意味である。いったん変な長い縦棒(積分)のことは置いておく
Fcが保存力である。保存力と移動(変位)によって位置エネルギーは定義される。
保存力とはなにか?「微小変位ベクトルで周回積分した場合経路によらず0になる」力のことであるが、これも難しいだろう。後に図を用いて感覚的に理解してもらうとしよう。
まずエネルギーとはなんだろうか?これは元々物理学の言葉で「仕事をする能力」という意味である。仕事もまた普通とは意味が違う。

物理学における仕事は力×移動距離で示される。つまり、荷物をもって突っ立てても仕事にはならないのだ。疲れるのに。

位置エネルギーは、これからするであろう、保存力の全仕事の見込み値なのでマイナスがつく。変な棒(積分)の前のマイナスはそれである。詳細は後に示す力学的エネルギー保存の法則を見るとわかるであろう。「とりあえず仕事に関係あるんだな」という認識でよい。
移動経路と力の向きがいつも同じとは限らない。力の向きが常に一定として、経路を自由にとるとする。

経路が自由ならば変位の向き(水色)は自由に変わってしまう。この時、経路①の仕事はどう考えればいいだろう?拡大して考えてみよう。
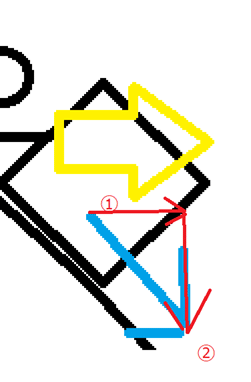
青い矢印は、赤い矢印①②に沿った移動の合計ともみて取れる。
力の方向と赤い矢印②は、向きが違うので仕事にはならない。①とは同じ向きなので、赤い矢印と黄色い矢印Fcの積が仕事になる。
青い矢印をごく短い移動、という意味でdr、①の大きさをdr1とすれば、この時の移動分の小さな仕事は

と数式で書ける。力と同じ方向の小さな移動だけ考えたわけだ。(r)がついているのは、力Fcが場所によって変わるかもしれないからだ。(関数は覚えているかな?)
今考えたのは青い矢印分の移動だけだったので、それを経路①全体で考えてみる。

この赤いでこぼことした移動を、ごくわずかな間隔で考え、先ほどの小さい仕事すべてを足し合わせる、というのが、仕事の線積分という意味になる。そう、積分(変な長い縦棒)とは大雑把に言えば、drに沿って何か変化するもの(Fc(r))について、細かく区切ったものを足し合わせることなのだ。

積分の上下の矢印のついたr、r0は位置を示している。わかりづらいなら地点ABでもなんでもよい。
さて、Fcの向きは常に右を向いていたので、青い矢印の右向きの部分だけ考えればよいのであった。
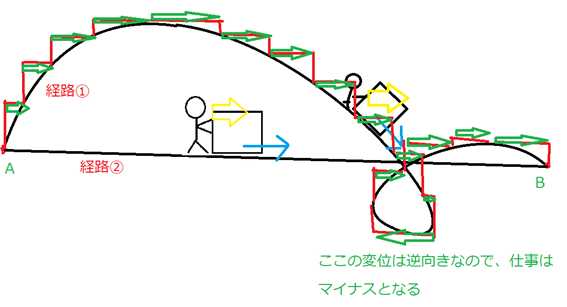
この緑の変位を足し合わせたら、経路②と同じではないだろうか?
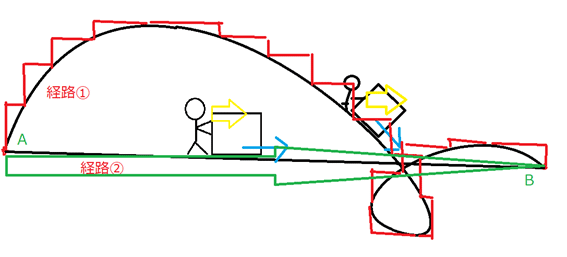
もし、Fc(r)が、縦方向に位置によらず一定ならば、経路①の仕事と経路②の仕事は完全に一致する。線積分の結果が経路によらず一定になる力を保存力というのだ。
なぜ一定になるのだろう?これは、黄色い矢印を最初に「右向きに固定」し、さらに大きさが「縦方向によらない」ことによっておきる。これらの性質は重力や万有引力に当てはまる。力の及び方の対称性が大きくかかわってくるのだ。


もし、黄色い矢印が変位と常に同じ向きだったらどうなるだろうか。青い矢印はわざわざ縦と横に分ける必要がなくなり、移動距離が長くなれば長くなるほど仕事は多くなるだろう。つまり、経路に依存する。

また、「向きは右だが、上に行くほど力の大きさが大きくなる力」ならどうなるだろう。そうなると上側を通ったときと下側を通った時で仕事が違ってしまう。やはり経路に依存する。

このように通常、仕事は経路に依存してしまう。仕事を求める際、どの経路をたどったかの情報が必要となる。だからこそ、最初と最後の位置さえわかってしまえば仕事がわかってしまう保存力は注目されるものであり、それによって蓄えられるエネルギーを位置エネルギーという。蓄えられるので、ポテンシャル(潜在的)エネルギーとも言う。
さて、最初に書いた位置エネルギーの式は向きの情報が含まれていたが、保存力の線積分は経路に依らない。つまり途中でどんな方向に変位が行こうがどうでもよいので、なるべく簡単にするために、力と同じ向きの、始点と終点の距離だけ考えた式に直そう。

これはr0からA地点までの、保存力と微小変位の積を足し合わせたものに見込みという意味でマイナス1をかけたものといえる。r0は基準点である。
基準点とはなんであろうか?基準点によって位置エネルギーの大きさは如何様にも変わるが、本質的にはどうでもよいものである。
まず積分の説明をしようか。具体例をもって図示した方がいいので保存力Fcは万有引力を採用しよう。

最初の式の万有引力にマイナスがついているのは、変位と力の向きが逆であることを意味する。結果的に万有引力の大きさを変位で積分する形になった。万有引力をy軸、変位をx軸、原点を地球の重心としてグラフの概形を書こう。

ここではグラフの形だけ知りたいので、GMm=10とした。そうでないとx軸の桁が7桁ほどになって見づらいことこの上ない。
先ほども述べたように、積分とは小さな間隔で区切った小さな仕事の足し合わせであった。それをグラフに示すと、
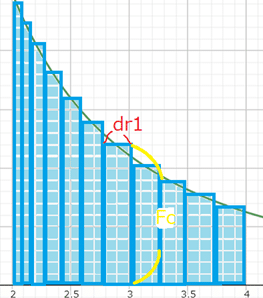
このようになる。r0=2からA=4の間で小さな仕事を足し合わせている。小さな仕事はFc(r)×dr1であった。(ここでのdr1は、変位drのうち力と同じ方向の部分を意味する)グラフにおいてそれはx軸から曲線までの縦の長さ(Fc)と小さな横の長さ(dr1)の掛算、つまり面積で表されることになる。dr1が極限まで小さければ、位置rが動くことによるFcの変化の影響を忠実に再現でき、結果として積分の値は

曲線とx軸が囲む面積の大きさになる。このことから、たとえA地点で重力が0だとしても、r0からAまで常に力が0でないならば、面積が0であるとは限らない。つまり位置エネルギーが0であるとは言えない。(ひろゆき氏の誤解①の反例)

さて、位置エネルギーと積分の関係がなんとなくわかったところで、基準点の話にもどろう。さきほどは例として万有引力を用いたが、この面積の具体的な求め方はまた長い説明が必要になるので、一定の力とみなせる重力で考えてみよう。

この時曲線とx軸が囲む図形は、長方形になるので、

と書ける。ここでのmgの前のマイナスは先の万有引力と同じく、変位の向きと反対向きの力であることを示す。
A-r0をhとすれば、中学校で見た位置エネルギーの公式mghとなる。
さて、上のグラフではr0を4にしたが、24ならどうなるか?

24の時は位置エネルギーがマイナスになってしまった。基準点が16であれば、上の位置エネルギーが0になるパターンである。つまり位置エネルギーは基準点で如何様にもかわってしまうのだ。
なぜこんな不安定な結果を導く基準点など採用するのか?それは、位置エネルギーは力学的エネルギー保存の法則など、ある状態からある状態への変化を前提として考えるからで、その過程で基準点の数値が消えてしまうからだ。力学的エネルギー保存の法則を見ていこう。

KA、UAはそれぞれ地点Aの運動エネルギー、位置エネルギー、KB、UBはそれぞれ地点Bの運動エネルギー、位置エネルギーである。運動エネルギーとは、動いている物体がもつエネルギーで、速度や質量が増すと運動エネルギーが増す。詳細は省略。
この式は「ある物体に保存力だけが働いている時、その力学的エネルギー(運動エネルギーと位置エネルギーの和)が保存される(一定である)」という意味である。エネルギーが保存される場の力、という意味で、保存力と言う名前なのだ。
さて、我々はもう位置エネルギーを具体的に記述できる。今回働く保存力は重力としようか

さて、上式を見れば、最終的にr0の情報が消えている。つまり状態Aから状態Bへの変化において基準点は関係がないのだ。変化を考えない単独の状態Aの位置エネルギーの公式だけでは、あまり物理的意味はない。
もう一つこの式から発見できることがある。左辺KB―KAは「運動エネルギーの変化量」、右辺-1×mg(B-A)は「-1×位置エネルギーの変化量」であった。
さて最初の方で位置エネルギーは「保存力がする仕事×-1」と言った。これを当てはめると、「-1×AB間で保存力がする仕事×-1」=「AB間で保存力がする仕事」。
つまり「保存力がした仕事分だけ、運動エネルギーが増える」という意味になる。仕事した分だけエネルギーが増えるのは、考えたら当然の話なのである。
位置エネルギーに概要が分かったところでひろゆき氏の誤解②を訂正させていただく。
ひろゆき氏の主張は放送回によって若干異なるので、発言を二つの捉え方で解釈できる。
② ―1「位置エネルギーはない。宇宙いって重力なくなるんだからまるっきり嘘」
② ―2「位置エネルギーはない。都合よいから概念上導入したもの。重力で説明すればよい」
一つ目は、本記事でも否定できるが、身近にある現象からもあきらかに否定できる。
ダムだ。
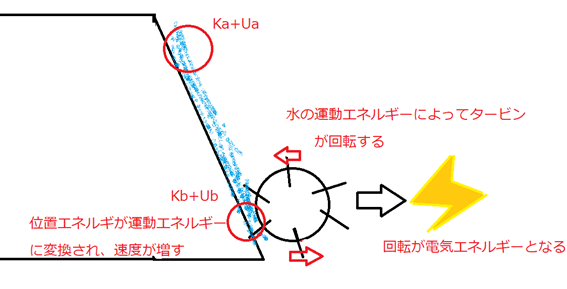
ダムとは水の位置エネルギーを運動エネルギーに変換し、タービンを回転させて電気エネルギーに変換している。もし位置エネルギーがまるっきり嘘なら、水力発電というシステムはこの世に存在しない。
二つ目は、あっているともいえるし、間違っているともいえる。なぜならエネルギーは物体や場が持っている状態であって、エネルギーそのものを可視化して表現はできない。様々な現象から、そこに蓄えられていることを類推することしかできない。
状態で定義しているものを存在するというのかどうかは、国語や哲学の話だろう。私はそれらの分野に明るくないので、だれか「ひろゆきでもわかる存在の定義(哲学)」で解説してくれないだろうか。
重力で説明すればよい、というのは物理学的には古典物理学に近い発想だろうか。一つの見方としては正しいと思うが、やはりそれだけではエネルギーや保存量の概念に到達しない。
古典物理学…ニュートンの運動方程式に対比して、解析力学におけるラグランジュの運動方程式というものがある。このラグランジュLは、L=K-Uを意味する。
古典力学の立場では表現しきれなかったことが、解析力学では表現できる、らしい。筆者も未だ勉強中の身なので多くは述べないが、この学問は電磁気学や相対論、量子力学、素粒子論の基礎になるといえば重要性が伝わるだろうか。
さて、稚拙ながらもひろゆき氏の誤解を解いてみたので、次によく見る誤解を解くとする。本旨ではないので懇切丁寧には解説しない。ちゃんとわかりたければある程度は自分で勉強する必要がある。主に数学を。
わからなかったら飛ばしてもよい(この部分を動画化するかは検討中)
・無限遠点とは何か
無限遠点とは万有引力やクーロン力など、逆二乗の力の基準点として採用される、無限に遠い点のことである。
万有引力の位置エネルギーは、地球の重心に原点を置くと、

であらわされる。この時、r0が無限だったらどうなるか?右辺第二項は0になる。圧倒的に見やすい。
また見やすいだけでなく①無限遠点より高くなることはないので、符号が固定されて比較しやすい②無限遠点はどの星から見ても無限の位置にあるので、二つ以上の星からの位置エネルギーを考慮する際、相対的な位置関係を考慮する必要がない
という理由でよく無限遠点が基準点に採用される。
・発散する点
上記の通り、無限遠点を基準点にとると、重心からr離れた位置には、

の位置エネルギーがある。これだと原点近くで、負の無限大にならないか?自然界で無限大に発散するのはおかしい、という疑問があった。
まあ自然界でもブラックホールの重力は無限大と言えるのだが、もちろん地球付近で無限大の現象があったら何が起きるかわからんので怖い。実はブラックホールとはまた違う理屈が存在する
皆、万有引力の法則の定義を覚えているだろうか?「二物体に相互作用し引き合う力」である。物体は細かく分割できる。原子と原子同士で引き合っているのだ。
ここでの分割は地殻と中心部だけにしようか。地球の中にある物質は、地殻と中心部両方から引っ張られている。地球の密度分布が球対称である場合、なんと、地殻が地球内部にある物体に対して働きかける万有引力は合計して0になるのだ。これは純粋な積分の結果から導かれる。
よって、その物体がある内側の球体分からの重力しかかからない。密度分布が一定ならば、グラフの概形は以下

この曲線は無限まで続くが、曲線と軸が囲む面積は有限に収束する。詳しくは広義積分でググってほしい。
よって重心の位置エネルギーは有限で、重力は0である。
・公転分の移動
地球は公転しているので、この分距離が縮まらないか?仕事は変わらないか?という疑問
以下は文献なしで考え、SNSで頂いたヒントを元にまとめた論なので、間違えていたら指摘して欲しい。
これは、地球が固定されていない座標系で考えている。
重力は場を形成し、空間を歪ませる。
地球が動いているとき、力の等高線は、ドップラー効果で見られるような歪んだ円を描く。そうなると、対称性が失われるので、仕事は経路に依存する。故に保存力と言えない。

ただし、これは地球だけが公転してもう一方の物体が公転していない状態の論である。実際はもう一方の物体も公転するので、相対的な距離は地球が固定された座標系で考察することとなんら変わりがない。なので、保存力とみなせる。
まとめ
ここまで読んでくださり、ありがとうございます。普段物理学から遠い所にいる人も楽しめたでしょうか?物理学を修めた方々は退屈だったかもしれません。数学が好きな方には、荒っぽい説明にひっかかりを覚えたかもしれません。
未だ学生の身であるので、間違い、指摘、質問等あれば遠慮なくコメント欄やtwitterに投げかけて頂けると幸いです。
参考文献:『考える力学』兵頭俊夫
