【ABC341】緑コーダーの競プロ参加記録 #3

igasu_7

2024年2月22日 22:00

「数学的な正しさより雰囲気のつかみやすさを優先した灰コーダー茶コーダー向けの記事があったらなぁ」

本記事は、そんな茶コーダーの頃の私の気持ちをベースにしています。

今回はAtCoder Beginner Contest 341。使用言語はPythonです。

【解説】 A問題 - Print 341

コンテスト中の提出
https://atcoder.jp/contests/abc341/submissions/50331282

正整数$${N}$$が与えられる
$${N}$$個の '0' と$${N+1}$$個の '1' からなる、'0' と '1' が交互に並んだ文字列を出力してね。

ABCのA問題では、プログラミング言語の基礎的な処理を問われることが多いです。この問題も例にもれず、入力・出力、文字列の扱い方が問われています。
まずは入力と出力から見ていきましょう。

Pythonではinput関数を利用することで入力を受け取ることができます。input関数は入力1行をまるまる文字列として受け取りますので、整数やリストを扱う問題では工夫が必要です。

出力はprint関数を利用します。ABCではprint関数で出力された値をユーザーの答えとして扱うので、必要以上にprint関数を実行して不正解にならないよう気を付けましょう。

""" 入力を受け取る """
S = input()

""" 問題を解く処理 """

""" 答えを出力 """
print(ans)

整数$${N}$$を入力から受け取ります。input関数で受け取った値は文字列なのでint関数で整数に変換しておきます。

""" 入力を受け取る """
N  = int(input())

さて求められている文字列は '1' の個数が '0' の個数より1つ多いです。
$${N}$$個の '01' あるいは '10' を作り、いい感じに残りの '1' をくっつけることを考えます。

文字列として扱うのであればこうなります。

""" 入力を受け取る """
N = int(input())

""" 問題を解く処理 """
ans = '10' * N + '1'

""" 答えを出力 """
print(ans)

forループを使ってもよいです。

""" 入力を受け取る """
N = int(input())

""" 問題を解く処理 """
ans = '1'
for _ in range(N):
    ans += '01'

""" 答えを出力 """
print(ans)

今回は問題になりませんが、実はPythonにおいて '+' 演算子で文字列を連結していると非常に時間がかかるケースがあります。そういった場合は一旦リストに文字をまとめておいて後でjoinする必要があります。

""" 入力を受け取る """
N = int(input())

""" 問題を解く処理 """
str_list = ['1']
for i in range(N):
    str_list.append('01')
ans = ''.join(str_list)

""" 答えを出力 """
print(ans)

今回の問題は1行で解くこともできます。

print('10' * int(input()) + '1')

$${N}$$個の '01' あるいは '10' を作る以外の解法もあります。

""" 2で割った余りを利用する """
N = int(input())
ans = [str((i + 1) % 2) for i in range(2 * N + 1)]
print(''.join(ans))

$${N \leq 100}$$なのでこんなこともできます。

""" 整数として扱う """
N = int(input())
ans = 1
for _ in range(N):
    ans = ans * 100 + 1
print(ans)

""" 二進数を利用する """
N = int(input())
mask = 0
for i in range(2 * N + 1):
    if i % 2 == 0:
        mask |= 1 << i
ans = bin(mask)[2:]
print(ans)

なお、この2つは$${N}$$が大きい場合には使えません。
気になる方は上のコードを$${N=200000}$$で試してみてください。

【解説】 B問題 - Foreign Exchange

コンテスト中の提出
https://atcoder.jp/contests/abc341/submissions/50339918

$${N}$$個の国がある。
国$${i}$$の通貨を$${A_i}$$円持っている。
国$${i}$$の通貨$${S_i}$$円を国$${i+1}$$の通貨$${T_i}$$円と何回でも交換できる。
国$${N}$$の通貨を最大で何円持てるか出力してね。

ぱっと見、D問題レベルかと思ってしまいます。
よく読むと最大化するのは国$${N}$$の通貨だけでよく、通貨の流れは国の番号が +1 ずつ大きくなる方向のみです。

お金の流れを逆から考えると、国$${N}$$の通貨を最大にするためには国$${N-1}$$の通貨を最大にする必要があり、そのためには国$${N - 2}$$の・・・と続き、結局は国$${2}$$の通貨を最大にすることに繋がります。

つまり$${i=1}$$から始めて、国$${i}$$の通貨を交換できるだけ全て国$${i+1}$$の通貨に交換すればよいです。

""""""
N = int(input())
A = list(map(int, input().split()))
for i in range(N - 1):
    s, t = map(int, input().split())
    p = A[i] // s
    A[i + 1] += t * p
print(A[N - 1])

【解説】 C問題 - Takahashi Gets Lost

コンテスト中の提出
https://atcoder.jp/contests/abc341/submissions/50347113

陸 or 海からなるグリッドが与えられる。
長さ$${N}$$の文字列$${T}$$に従って陸を移動可能。
移動後のマスとして考えられるものの個数を出力してね。

全探索すればよさそうですが、$${H,W≤500, N≤500}$$なので$${O(HWN)}$$解法は計算量が$${500^3 = 1.25 \times 10^8}$$になり 2 sec だと間に合うか微妙です。

ここで問題ページをよく見ると「実行時間制限: 3 sec」とあり、PyPyであれば間に合うかもしれません。

というわけで開始地点を全探索して移動をシミュレーションします。
グリッドを移動するタイプの問題では、移動用のリストを用意すると実装が少し楽になります。

問題の指示通りのコードを提出すると2919msでした。C問題でこんなギリギリになるの・・・？

コンテスト後に何回か提出しているとPyPyでも 2999ms とか出たので、ジャッジサーバーの機嫌によっては運悪くTLEになることもあるのかもしれません。

TLEはdictのせい？

こんなに時間ギリギリなんて問題設定上どうなんだろうとモヤモヤしつつもACになったから良いか、と過ごしていたところTwitterで「Pythonでdictを使ってTLEになった」と言っている方を見かけました。

私はdictを使ってもACになっているのでどういうことだろう？と思って色々と試してみると・・・左がAC ( = 2700 ms) で右がTLE ( > 3300 ms) です。

そもそもdictを使わず書くと 1800 ms でした。

""" dictを使わない """
for t in T:
    d = 0
    if t == 'R':
        d = 1
    elif t == 'U':
        d = 2
    elif t == 'D':
        d = 3
    u += Di[d]
    v += Dj[d]

dictへのアクセスでそんなに差が出るかなぁ？と思って、dictのキーをstrからintに変更してみると 1800ms。if を使うのと同等になりました。
やっぱり文字列をdictのキーにすると遅い？

""" dictのキーを int にする """
P = {}
for i, t in enumerate('LRUD'):
    P[ord(t)] = i

""" 中略 """

        for t in T:
            u += Di[P[ord(t)]]
            v += Dj[P[ord(t)]]

かなり回りくどく、dictをリストで代用してみると1500ms。

""" dictをリストで代用 """
M = max(map(ord, 'LRUD'))
P = [0] * (M + 1)
for i, t in enumerate('LRUD'):
    P[ord(t)] = i

""" 中略 """

        for t in T:
            u += Di[P[ord(t)]]
            v += Dj[P[ord(t)]]

ordを通してdictにアクセスするくらいなら最初から文字列$${T}$$のほうをintのリストにしておけばいいのでは？
これがなんと 600ms でした。$${O(HWN)}$$だけあって、たかがif 文、リストアクセスでもかなりの時間を食っていたようです。
まぁ$${O(1)}$$の処理でも$${1.25 \times 10^8}$$回くらい実行されますもんね。たしかに。

""" T を int のリストに変換 """
T = list(input())
P = {'L': 0, 'R': 1, 'U': 2,'D': 3}
for i in range(N):
    T[i] = P[T[i]]

""" 中略 """

        for d in T:
            u += Di[d]
            v += Dj[d]

「想定解で時間ギリギリなんてひどい問題だ！」

と、正直思っていましたが「どの処理にどれだけ時間がかかっているかちゃんと理解してますか？」という公式からの問いかけだと思えば良い問題だと思えるかもしれません。

いや。

【余談】
コンテスト後に気付きましたが私の提出コードは結構めちゃくちゃなことをしていて、必要のない番兵を外周に置いている上にループは[0, H), [0, W)のままです。問題設定上たまたまACになっていますが、問題文はよく読みケアレスミスにも注意しないといけないですね。

【解説】 D問題 - Only one of two

コンテスト中の提出
https://atcoder.jp/contests/abc341/submissions/50369253

正整数$${N, M, K}$$が与えられる。
$${N}$$と$${M}$$どっちか片方のみで割り切れる$${K}$$番目の正整数を出力してね。

まずは簡単なところから

「正整数」とあるので 0 は含まれません。

まず$${N}$$についてのみ考えてみます。$${N}$$の倍数のうち$${k}$$番目の正整数を$${X}$$とすると、$${X=kN}$$と表せます。
たとえば、3の倍数の2番目は6であり、10の倍数の5番目は50です。

これの逆を考えてみます。6が2番目の3の倍数であるということは、1から6までの数の中に3の倍数が2つ含まれることになります。
では1から5までの数の中に3の倍数はいくつあるかというと1つです。これを計算式で表すと$${\large \lfloor \frac{5}{3} \rfloor}$$$${ = 1}$$です。

つまり$${X}$$以下の$${N}$$の倍数は$${\large \lfloor \frac{X}{N} \rfloor}$$個あります。

$${\lfloor A \rfloor}$$は$${A}$$を切り捨てした値 ($${A}$$の整数部分) を表します。

互いに素なN, M

上記をもとに$${N, M}$$が互いに素な場合、つまり1以外に共通の約数を持たない場合における「$${N}$$と$${M}$$どっちか片方のみで割り切れる正整数の個数」について考えます。ある正整数$${X}$$について、

$${X}$$以下の$${N}$$の倍数は$${P=\large \lfloor \frac{X}{N} \rfloor}$$個あります。
$${X}$$以下の$${M}$$の倍数は$${Q=\large \lfloor \frac{X}{M} \rfloor}$$個あります。
$${X}$$以下の$${NM}$$の倍数は$${R=\large \lfloor \frac{X}{NM} \rfloor}$$個あります。

$${NM}$$の倍数は「$${N}$$の倍数かつ$${M}$$の倍数」であり、$${N}$$の倍数の中にも$${M}$$の倍数の中にも含まれますのでその両方から除外します。
よって「$${N}$$の倍数または$${M}$$の倍数である数のうち$${NM}$$の倍数を除いた正整数の個数」すなわち「$${N}$$と$${M}$$どっちか片方のみで割り切れる正整数の個数」は$${(P-R)+(Q - R)}$$と表せます。

$${X}$$を全探索すれば問題を解けそうですが、いかにも$${X}$$の値が大きくなりそうで全探索できませんので二分探索を使います。「求めたい整数は$${X}$$以下ですか？」という判定問題を考え、$${(P-R)+(Q - R) \geq K}$$を判定することでこの問題を解くことができます。

Pythonは整数の上限がないので二分探索する区間の最大値は適当に大きな数を設定しておけばOKで、たとえば$${10^{10000}}$$でもACになります。なお公式解説に答えの上限が$${2 \times 10^{18}}$$であることの証明が掲載されています。

互いに素でないN, M

ところで$${N, M}$$が互いに素でない場合、つまり共通の約数を持つ場合はどうでしょうか。ある正整数$${X}$$について、

$${X}$$以下の$${N}$$の倍数は$${P=\large \lfloor \frac{X}{N} \rfloor}$$個あります。
$${X}$$以下の$${M}$$の倍数は$${Q=\large \lfloor \frac{X}{M} \rfloor}$$個あります。

ここまでは変わりません。除外する正整数の個数$${R}$$はいくつかになるかを考えます。

ここで$${N, M}$$の最大公約数 (gcd) を$${g}$$とおき、$${N = gN', M = gM'}$$とすると、$${N', M'}$$は互いに素な正整数であり、$${N', M'}$$について前節と同様に考えることができそうです。

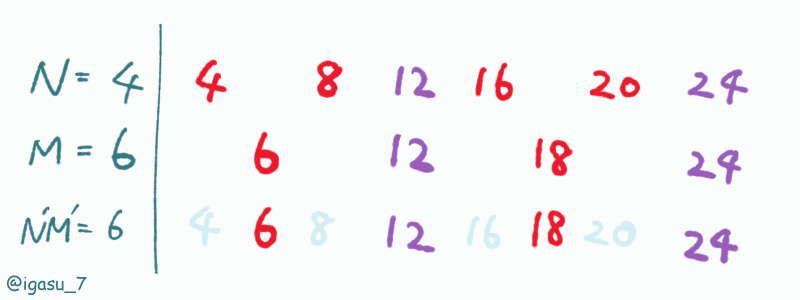
しかし、実際には$${N'M'}$$の倍数は「$${N}$$の倍数かつ$${M}$$の倍数」を常に満たすとは限りません。なぜなら$${N, M}$$の最大公約数$${g}$$が抜けたままだからです。なんとか$${g}$$を仲間に入れてあげたいです。

ところで、$${gN' = N, gM' = M}$$より$${gN'M'}$$は「$${gN'}$$の倍数かつ$${gM'}$$の倍数」すなわち「$${N}$$の倍数かつ$${M}$$の倍数」であり、かつその最小の正整数です。よって$${gN'M'}$$の倍数について考えればよさそうです。つまり、

$${X}$$以下の$${gN'M'}$$の倍数は$${R=\large \lfloor \frac{X}{gN'M'} \rfloor}$$個あります。

この場合も、求めたい整数の個数は$${(P-R)+(Q - R)}$$個あります。

解答

最大公約数は標準ライブラリのmathモジュールからgcd関数を使うのが楽です。
$${N, M}$$が互いに素の場合では$${g = 1, N = N', M=M'}$$なので、全てのケースにおいて$${N', M'}$$を考えてよいです。

from math import gcd
def solve(x):
    """ 答えは x 以下か？ """
    p = x // N
    q = x // M
    r = x // (g * n * m)
    res = p + q - 2 * r
    return res >= K

N, M, K = map(int, input().split())
g = gcd(N, M)
n = N // g
m = M // g

""" 二分探索 """
ng, ok = 0, 10 ** 10000
while ok - ng > 1:
    mid = (ng + ok) // 2
    if solve(mid):
        ok = mid
    else:
        ng = mid
print(ok)

【余談】

$${gN' = N, gM' = M}$$より$${gN'M'}$$は「$${gN'}$$の倍数かつ$${gM'}$$の倍数」すなわち「$${N}$$の倍数かつ$${M}$$の倍数」であり、かつその最小の正整数です。

これを簡潔に言うと、
$${N,M}$$の最大公約数$${g}$$に対して$${gN'M'}$$は$${N,M}$$の最小公倍数です。

また$${N,M}$$の最小公倍数を$${l}$$とすると、

$$
l = gN'M' = \frac{gN'gM'}{g} = \frac{NM}{g}
$$

より、$${NM = lg}$$です。

この関係を知っていると最大公約数から最小公倍数へと考察を切り替えることが容易になります。競プロにおいては最小公倍数より最大公約数のほうが汎用性が高い（と思っている）ので、考察ステップを簡略化する意味で知っていると便利です。

解説はここまでです。ありがとうございました。

E - Alternating String

0 と 1 が交互になっていると良い文字列。
$${Q}$$個のクエリが与えられる。
クエリ 1: 区間$${[L, R]}$$の 0 と 1 をすべて反転させる。
クエリ 2: 区間$${[L, R]}$$が良い文字列かどうか判定してね。

3週連続でE問題セグ木ですね～。

問題文を素直に読むと区間全体に対して操作するタイプっぽいので区間更新の遅延セグ木でなんやかんやしようとするも実装が上手くいかず。

問題文を読み換えると1点更新のセグ木でよかったんですね。

でもまぁ今までなら実装したくてもできない状態なので、解けなかったものの1歩進んでいるということで前向きに。

あとがき

今回のコンテストの結果はABCD4完46分、順位は2366位、1120 perfでした。

前回文字を書きすぎたのを少し反省しています。

ではまた～。