
【ABC347】緑コーダーの競プロ参加記録 #9
しばらくの間、コンテスト直後にざっくりとした記事を投稿しつつ、詳細な解説をちまちま追記していくスタイルで記事を制作しようと思います。
今回はAtCoder Beginner Contest 347。使用言語はPythonです。
A問題 - Divisible
コンテスト中の提出
https://atcoder.jp/contests/abc347/submissions/51800824
正整数$${K}$$と、数列$${A}$$が与えられる。
$${A}$$の要素のうち$${K}$$の倍数であるものを$${K}$$で割った値を出力してね。
$${K}$$の倍数の判定は、$${K}$$で割った余りが$${0}$$かどうかを考えます。
割り算を '/' で行うと float 型になってしまい WA になります。
これは小数誤差ではなく、5 が 5.0 と出力されることが原因なので int 関数で整数に変換すれば AC を得られます。
なお、切り捨て除算 '//' を行うと整数のまま処理できます。
""" AC コード """
N, K = map(int, input().split())
A = list(map(int, input().split()))
ans = []
for a in A:
if a % K == 0:
ans.append(a // K)
print(*ans)
A問題にしては引っかかるポイントが多くて難しい気がします。
制約を確認して、$${K}$$が$${0}$$でないかどうかも注意しましょう。
B問題 - Substring
コンテスト中の提出
https://atcoder.jp/contests/abc347/submissions/51807303
文字列$${S}$$が与えられる。
$${S}$$の部分文字列の種類数を出力してね。
ぱっと見、D問題レベルのことを問われている気がしてびっくりしました。
部分文字列の長さとスタート位置の組み合わせを全探索することで、考えられる部分文字列を全列挙できます。
これを set 型で重複なくカウントします。
""" AC コード """
S = input()
N = len(S)
res = set()
for length in range(1, N + 1):
for i in range(N):
res.add(S[i:i+length])
ans = len(res)
print(ans)
Pythonのスライスは始点、終点ともに元の文字列のインデックスをはみ出していてもエラーになりません。
ただし、始点がはみ出していると空文字が返ってくるので今回の問題では注意が必要です。
""" スライス の挙動 """
S = 'abcd'
i = 1000000000000
T = set()
T.add(S[i:i * 2])
T.add(S[2:i * 2])
print(T)
"""
>>> {'', 'cd'}
"""Pythonの set から要素を取り除くときは discard() を使うか、存在判定をしてから remove() します。
存在しない要素に対して remove() するとエラーになります。
""" set の discard と remove """
T = set()
T.add('abcd')
T.discard('')
T.remove('')
"""
>>> line 6, in <module>
>>> T.remove('')
>>> KeyError: ''
"""C問題 - Ideal Holidays
解けませんでした!!!!!!!!!!!!
1週間のうち前半の$${A}$$日間が休日で、後半の$${B}$$日間が平日。
$${i}$$番目の予定は今日から$${D_i}$$日後。
今日が何曜日かは不明。
すべての予定が休日である可能性があるか判定してね。
$${n}$$日後が休日かどうかを判断するには曜日だけ考えればよいです。
1週間が$${A+B}$$日なので、予定日を$${\mathrm{mod} (A+B)}$$で考えます。
数列$${D}$$の要素をそれぞれ$${A+B}$$で割った余りで置き換えます。
同じ曜日の予定は1つにまとめてよいので重複を削除します。
曜日を早い方から順に並べると見通しが良くなるのでソートします。
この操作で得られる数列を$${E}$$として、$${E}$$の長さを$${K}$$とします。
""" 予定日を mod (A + B) で考える """
N, A, B = map(int, input().split())
D = list(map(int, input().split()))
mod = A + B
for i in range(N):
D[i] %= mod
E = sorted(set(D))
K = len(E)
さて、すべて休日になる条件はなんなのでしょう。
パッと思いつくのは「$${E}$$の最大値と最小値の差が$${A}$$未満」ですが、これは以下の図のケースでWAになります。
""" WA 解法 """
if max(E) - min(E) < A:
print('Yes')
else:
print('No')$$
\mathrm{max}(E) - \mathrm{min}(E) = 10 - 1 = 9 > A = 6
$$

解法 1: 予定全体の幅を考える
$${\mathrm{max}(E) - \mathrm{min}(E)}$$が何を表すか考えてみると「予定全体の幅」と言えます。
「予定全体が休日の幅に収まるかどうか」を考えるのは考察として正しいです。WA になるのは「予定全体の幅」の求め方に原因がありそうです。
上の解法でACを得るためには、予定をいい感じに平行移動して「予定全体の幅の最小値」を考える必要があります。
「予定全体の幅」の左端を全探索して、$${K}$$個の予定全体の「幅の最小値」を求めることでACを得られます。
予定日を含む区間の幅なので、両端を含めるよう予定日の差から +1 します。
""" 予定全体の幅の最小値を求める """
mod = A + B
E = sorted(set(D))
K = len(E)
min_length = 1 << 60
for i in range(K):
j = (i + K - 1) % K
length = (E[j] - E[i]) % mod + 1
min_length = min(min_length, length)
if min_length <= A:
print('Yes')
else:
print('No')解説用コードの全体https://atcoder.jp/contests/abc347/submissions/51924033
Pythonであれば、負の値の余りを正整数として返してくれるので計算が楽です。
解法 2: 平日分のスキマを考える
解法 1 では「予定全体が休日の幅に収まるかどうか」を考えました。
この発想を逆転すると、「どこかに平日がすべて収まるスキマがあるかどうか」を考えることと同じです。

解法 1 と同様に、ありうるすべてのスキマの長さを求めて$${B}$$と比較します。
予定と予定に挟まれている区間の幅なので、両端を含めないよう予定日の差から -1 します。
$${0 - 1 \mathrm{mod}(A + B) = A + B - 1 >= B}$$であり、$${E}$$の要素数が$${1}$$でも問題ありません。
""" 平日分のスキマを考える """
mod = A + B
E = sorted(set(D))
K = len(E)
for i in range(K):
j = (i + 1) % K
length = (E[j] - E[i] - 1) % mod
if length >= B:
print('Yes')
exit()
print('No')解説用コードの全体
https://atcoder.jp/contests/abc347/submissions/51924380
公式解説も本質的にはこの解法と同じですが、$${E}$$の要素数が$${1}$$のとき予定日の差が$${0}$$となり、'Yes' であるはずが 'No' と出力されてしまうことに気を付けます。
解法 3: 予定を2倍の長さで考える
1週間はグルグル回り続けます。つまり「円環」とみなせます。
円環を考える問題の典型テクニックとして、「長さ2倍の列に置き換える」というものがあります。
(参考) 競プロ典型90問: 076 - Cake Cut(★3)

解法 1 も解法 2 も、予定日の差を$${\mathrm{mod} (A + B)}$$で考えるため重複削除が必須だったり、$${E}$$の要素数が$${1}$$の場合などWAの原因になりうるポイントがあります。
これに対し2倍の長さの列として捉えると、予定日の差をそのまま考えるだけでよいので悩むことが少なくなります。
重複削除もしなくてよいです。
2倍の長さと言いますが、解法 2 の判定方法であれば$${E}$$の末尾に$${E[0] + A + B}$$を追加するだけでよいです。
""" 円環を2倍の長さの列とみなす """
N, A, B = map(int, input().split())
D = list(map(int, input().split()))
mod = A + B
for i in range(N):
D[i] %= mod
D.sort()
D.append(D[0] + A + B)
for i in range(N):
length = D[i + 1] - D[i] - 1
if length >= B:
print('Yes')
exit()
print('No')解説用コードの全体
https://atcoder.jp/contests/abc347/submissions/51924778
【余談】
めちゃめちゃ難しいC問題だったと思います。
私が最初にパッと思いついたのは max - min 解法だったのですが、ダメなケースに気付いて提出もせずD問題に進みました。
コンテスト後に提出してみると 1 WA。
コーナーケースというほどの特殊例でもないはずですが、これで 1 WA だと「やり方は合ってるんだ!」と沼にハマってしまいそうです。
D問題 - Popcount and XOR
コンテスト中の提出
https://atcoder.jp/contests/abc347/submissions/51851807
非負整数$${a, b, C}$$が与えられる。
すべての条件を満たす非負整数$${X,Y}$$があれば1つ出力してね。
条件1: $${0 \leq X, Y < 2^{60}}$$
条件2: $${\mathrm{popcount}(X) = a, \mathrm{popcount}(Y) = b}$$
条件3: $${X \oplus Y = C}$$
$${0 \leq C < 2^{60}}$$なので、この節では「足りない部分は$${0}$$で埋めた60桁の二進数」について考えることにします。
$${X \oplus Y}$$は「$${X}$$と$${Y}$$の排他的論理和 (XOR)」を表します。
XORの挙動を再確認するところから考察をスタートします。

$${X \oplus Y = C}$$を満たすためには、
$${C}$$のビットが$${1}$$である桁では、$${X, Y}$$どちらか一方のみ$${1}$$
$${C}$$のビットが$${0}$$である桁では、$${X, Y}$$どちらも$${0}$$または どちらも$${1}$$
である必要があります。
$${\mathrm{popcount}(C) = K}$$とします。
forループでひとつずつカウントしてもよいですが、Pythonであればbit_count()で求められます。
$${C}$$のビットが$${1}$$である$${K}$$個の桁のうち、$${x}$$個の$${1}$$を$${X}$$に、$${y}$$個の$${1}$$を$${Y}$$に割り当てると仮定します。
$$
y = K - x
$$
このとき、$${C}$$のビットが$${0}$$である$${60 - K}$$個の桁のうち、$${X}$$では$${a - x}$$個、$${Y}$$では$${b - y}$$個の桁が$${1}$$である必要があります。
$${X, Y}$$ともに同じ桁について$${1}$$を割り当てるため、その桁数は一致していなければなりません。
$$
a - x = b - y \\
0 \leq (a - x, b - y) \leq 60 - K
$$
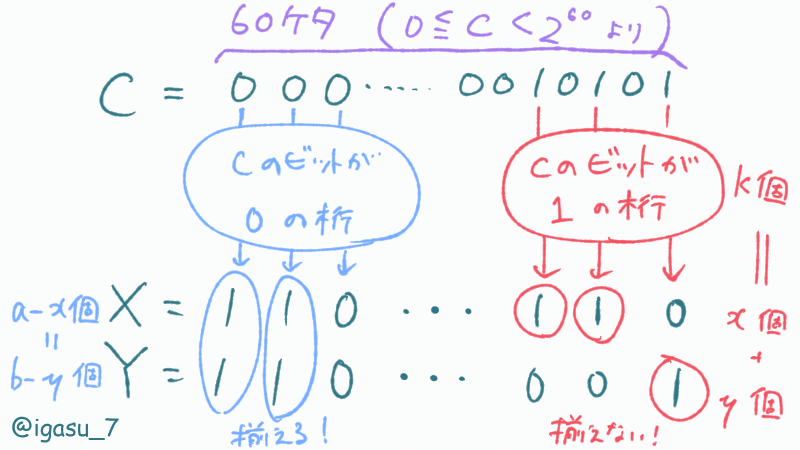
$${x, y}$$の組み合わせを全探索することで解きます。
そのあとは桁の小さい方から貪欲にビットを$${1}$$にしていけばよいです。最初から最大60桁であると決めておくと自然に$${0 \leq X, Y < 2^{60}}$$の条件を満たします。
""" AC コード """
a, b, C = map(int, input().split())
k = C.bit_count()
for x in range(k + 1):
y = k - x
if a - x == b - y and 0 <= a - x <= 60 - k:
X, Y = 0, 0
xx, yy, zz = x, y, a - x
for bit in range(60):
if xx == 0:
break
if (C >> bit) & 1 == 1:
xx -= 1
X |= (1 << bit)
for bit in range(60):
if yy == 0:
break
if (C >> bit) & 1 == 1 and (X >> bit) & 1 == 0:
yy -= 1
Y |= (1 << bit)
for bit in range(60):
if zz == 0:
break
if (C >> bit) & 1 == 0:
X |= (1 << bit)
Y |= (1 << bit)
zz -= 1
print(X, Y)
exit()
print(-1)ちなみに、bit_count() が使えるのは Python3.10 以降です。
E問題 - Set Add Query
コンテスト中の提出
https://atcoder.jp/contests/abc347/submissions/51871385
$${Q}$$個のクエリが与えられる。
操作 1: $${S}$$に$${x_i}$$が含まれないなら、$${S}$$に$${x_i}$$を追加。
操作 2: $${S}$$に$${x_i}$$が含まれるなら、$${S}$$から$${x_i}$$を削除。
操作の後、$${S}$$に含まれるすべての$${x}$$について$${A_x}$$に$${|S|}$$を加算。
最終的な数列$${A}$$を出力してね。
あるタイミングで集合に含まれるすべての整数について一気に処理をしようとすると大変です。
$${i}$$番目のクエリで整数$${x_i}$$が集合に追加されてから、$${j}$$番目のクエリで取り除かれるまでの$${j - i}$$回、各タイミングにおける集合の要素数$${|S|}$$が$${A_{x_i}}$$に加算され続けます。
$${i}$$番目のクエリで数列$${A}$$に加算される要素数$${S_i}$$は素直に調べていくことで$${O(Q)}$$で求められます。
$${i}$$番目のクエリから$${j}$$番目のクエリまでの$${j - i}$$回の間に加算される数の総和はこれの区間和になるため、累積和をとります。

ある整数$${x_i}$$が出現する位置をそれぞれ求めておき、集合に含まれている間のみ区間和を加算していくことで解けます。
区間を以下のように捉えると少し楽になる気がします。
$$
[i, j) = [i, Q] - [j, Q]
$$
""" AC コード """
from collections import defaultdict
from itertools import accumulate
N, Q = map(int, input().split())
X = list(map(int, input().split()))
""" 各 x の出現位置を調べる """
D = defaultdict(list)
for i, x in enumerate(X):
D[x].append(i)
""" i 番目のクエリ後における S の要素数を調べる """
Cnt = [0] * Q
S = set()
for i, x in enumerate(X):
if x in S:
S.remove(x)
else:
S.add(x)
Cnt[i] = len(S)
""" 要素数の累積和をとって、各 x ごとにクエリを再現 """
acc = list(accumulate(Cnt, initial=0))
A = [0] * N
for x, ids in D.items():
for turn, i in enumerate(ids):
if turn % 2 == 1:
A[x - 1] -= acc[Q] - acc[i]
else:
A[x - 1] += acc[Q] - acc[i]
print(*A)あとがき
今回はC問題が解けず、ABDE 4完 107分で 1968位、1232 perf。初めてレーティングが 1000 を超えました。
うれしいね。
3月はトータルで見てABCのパフォーマンスが良かった印象です。
ABCだけ見るとレーティング収支が$${\Large+ 129}$$。
ARCでレートを下げることでABCで無限の成長を感じられるライフハック。
解説を書くようになったおかげか、ARC参加を増やして考察寄りの問題に触れたおかげか、以前より解法が思い浮かびやすくなっている気がします。
ではまた~。


【更新履歴】
2024/03/31 (1時頃): 記事を投稿
2024/03/31 (21時頃): 一部文章を追加
2024/04/01 (3時頃): C問題の解説を追加
2024/04/01 (19時頃): B問題の解説を追加。全体の文章を調整。完成!
この記事が気に入ったらサポートをしてみませんか?
