
【ABC358】緑コーダーの競プロ参加記録 #23
今回はAtCoder Beginner Contest 358。使用言語はPythonです。

A問題 - Welcome to AtCoder Land
コンテスト中の提出
https://atcoder.jp/contests/abc358/submissions/54552054
文字列$${S,T}$$が与えられる。
$${S =}$$ 'AtCoder'、$${T =}$$ 'Land' かどうか判定してね。
やります。
""" AC コード """
S, T = input().split()
if S == "AtCoder" and T == "Land":
print('Yes')
else:
print('No')B問題 - Ticket Counter
コンテスト中の提出
https://atcoder.jp/contests/abc358/submissions/54559479
$${N}$$人がチケットを買う。
$${i}$$番目の人は時刻$${T_i}$$にチケット売り場の列に並ぶ。
チケットの購入手続きには$${A}$$秒かかる。
$${i}$$番目の人がチケットを購入する時刻をすべて出力してね。
$${i}$$番目の人は、待ち時間が無ければ時刻$${T_i + A}$$にチケットを購入します。
待ち時間があった場合、これまでに経過した時間$${x}$$に対して時刻$${x + A}$$にチケットを購入します。
「これまでに経過した時間$${x}$$」とは、「1つ前の人がチケットを購入した時刻」と同じです。
よって、前の人のチケット購入時刻をメモしながら処理を進めます。
""" AC コード """
N, A = map(int, input().split())
T = list(map(int, input().split()))
ans = 0
x = 0
for t in T:
if t > x:
ans = t + A
else:
ans = x + A
print(ans)
x = ans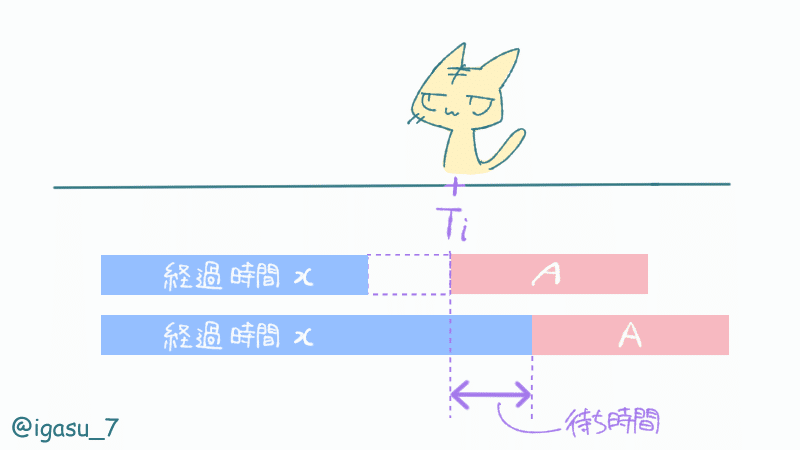
C問題 - Popcorn
コンテスト中の提出
https://atcoder.jp/contests/abc358/submissions/54565467
$${N}$$個のポップコーン売り場と、$${M}$$種類のポップコーンがある。
$${i}$$番目の売り場の品揃えは$${S_i}$$。
全種類のポップコーンを食べるために訪れる売り場の最小数を出力してね。
訪れるポップコーン売り場の選び方は$${2^N}$$通りあります。
$${N \le 10}$$であり$${2^N}$$通り調べることができるので、bit全探索をします。
ビットマスクの$${i}$$桁目が「$${1}$$なら$${i}$$番目のポップコーン売り場に訪れる」、「$${0}$$なら訪れない」とします。
訪れる全ての売り場で売っているポップコーンの種類をカウントし、その種類数が$${M}$$であったとき、答えを更新すればよいです。
種類数を数えるときは重複削除のため set を使い、訪れた売り場の個数は ビットマスクの$${1}$$である桁の個数を数えます。
""" AC コード """
N, M = map(int, input().split())
S = [input() for _ in range(N)]
ans = 999999
for mask in range(1 << N):
res = set()
for i in range(N):
if (mask >> i) & 1 == 1:
for j in range(M):
if S[i][j] == 'o':
res.add(j)
if len(res) == M:
ans = min(ans, mask.bit_count())
print(ans)
D問題 - Souvenirs
コンテスト中の提出
https://atcoder.jp/contests/abc358/submissions/54572999
$${N}$$個の箱がある。
$${i}$$番目の箱は$${A_i}$$円で、$${A_i}$$個のお菓子が入っている。
$${j}$$番目の人には$${B_j}$$個以上のお菓子が入った箱を渡したい。
同じ箱は複数購入できない。
必要な最小金額を出力してね。
必要なお菓子の個数が少ない人には、安い箱を渡せばよいです。
(証明については公式解説をご覧ください。)
$${A, B}$$ともに小さい方から順に見たいのでソートします。
ソート後の$${A, B}$$について、$${A_i \ge B_j}$$であるものがあれば箱$${i}$$を人$${j}$$に渡します。
「同じ箱は複数購入できない」という条件があるので、後戻りしない探索法である尺取り法を使います。
選べる箱がない人がいれば答えは$${-1}$$です。
""" A, B をソート """
N, M = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))
A.sort()
B.sort()
""" しゃくとり法 """
ans = 0
i = 0
for j in range(M):
while i < N and A[i] < B[j]:
i += 1
if i == N:
print('-1')
exit()
ans += A[i]
i += 1
print(ans)
E問題 - Alphabet Tiles
upsolve
https://atcoder.jp/contests/abc358/submissions/54618163
正整数$${K}$$と、長さ$${26}$$の数列$${C}$$が与えられる。
$${i}$$番目のアルファベットは$${0}$$個以上$${C_i}$$個以下使える。
長さ$${1}$$以上$${K}$$以下の文字列の個数を出力してね。$${\pmod{998244353}}$$
長さ$${j}$$の文字列について、$${1}$$番目から$${i}$$番目までのアルファベットのみを使って作ることを考えます。
$${i}$$番目のアルファベットを$${k}$$個使うと決めたとき、その$${k}$$文字の配置方法は$${_j\mathrm{C}_k}$$通りあります。
残りの$${j - k}$$文字について、$${1}$$番目から$${i - 1}$$番目までのアルファベットのみを使うことになりますが、これは上と同様の考え方ができます。

つまり、以下のようなDPで解くことができます。
$$
dp[i][j]: i 番目までのアルファベットで作れる長さjの文字列の個数
$$
遷移は以下のようになります。
$$
dp[i][j] \xleftarrow{+} dp[i - 1][j - k] \times _j\mathrm{C}_k
$$
$${_j\mathrm{C}_k}$$の計算を$${O(1)}$$で出来るように前計算しておきます。
$${_n\mathrm{C}_k = {\Large\frac{n!}{k! (n-k)!}}}$$であり、mod の世界で分数の計算をするため逆元を求める必要があります。
Python であれば pow 関数の第2引数を $${-1}$$にすればよいです。
""" 二項係数 nCk の前計算 (mod 998244353) """
def get_fact(n):
fact = [0] * (n + 1)
inv = [0] * (n + 1)
fact[0] = 1
inv[0] = 1
for i in range(1, n + 1):
fact[i] = fact[i - 1] * i % mod
inv[i] = pow(fact[i], -1, mod)
return fact, inv
def nCk(n, k):
return fact[n] % mod * inv[k] % mod * inv[n - k] % mod
""" 入力を受け取る """
K = int(input())
C = list(map(int, input().split()))
mod = 998244353
fact, inv = get_fact(K)今回、DPの$${i}$$はひとつ前のものしか参照しないので、リストを分割して実装しました。
各アルファベットには使用数の上限があることに注意が必要です。
すべてのアルファベットを使って作れる長さ$${j}$$の文字列の個数の総和が答えになります。
"""
dp[j]: i 番目までのアルファベットで作れる、長さ j の文字列の個数
"""
dp = [0] * (K + 1)
dp[0] = 1
for i in range(26):
ndp = [0] * (K + 1)
for j in range(K + 1):
for k in range(C[i] + 1):
if j < k:
break
ndp[j] += dp[j - k] * nCk(j, k) % mod
ndp[j] %= mod
dp = ndp
""" 答えを求める """
ans = 0
for j in range(1, K + 1):
ans += dp[j]
ans %= mod
print(ans)G問題 - AtCoder Tour
upsolve
https://atcoder.jp/contests/abc358/submissions/54625180
$${H\times W}$$のグリッドが与えられる。
$${(S_i, S_j)}$$からスタートして、$${K}$$回移動する。
$${(i, j)}$$に移動した時スコア$${A_{i,j}}$$を得る。
スコアの最大値を出力してね。
G問題にしてはとっつきやすそうなのでやってみました。
(F問題は出力形式が理解できません。)
$${t}$$ターン使ってマス$${(i, j)}$$に移動することを考えます。
マス$${(i, j)}$$に到達するまでのスコアを最大化するのはDPで解くことができます。
マス$${(i, j)}$$に移動した後は、残りの$${K - t}$$ターンをマス$${(i, j)}$$に留まって過ごします。
この行動に基づいてスコアを計算し、その最大値を求めればよいです。
ここで、マス$${(i, j)}$$に移動するとき最短ルートである必要はないこと、$${K \le 10^9}$$であることの2点に注意が必要です。
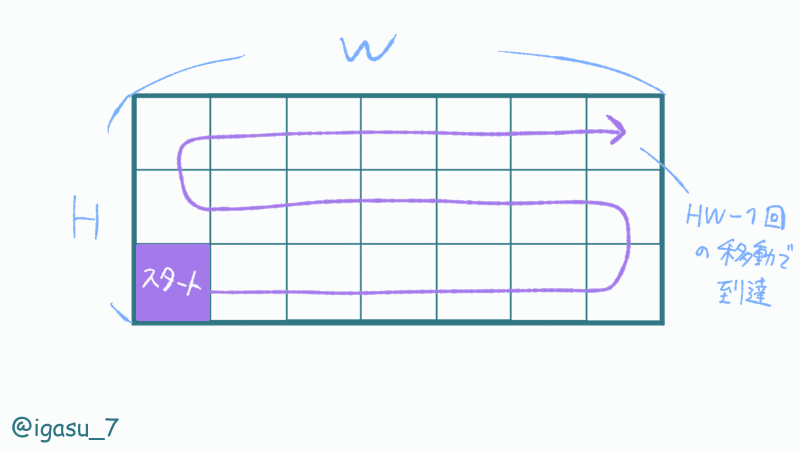
$${t}$$の全探索は、大きくても$${H \times W - 1}$$あれば十分です。
""" 入力を受け取る (si, sj を 0-index に変換) """
H, W, K = map(int, input().split())
si, sj = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(H)]
si -= 1; sj -= 1
""" DP用のあれこれ """
inf = 1 << 60
T = min(K, H * W - 1)
Di = [1, -1, 0, 0]
Dj = [0, 0, 1, -1]
"""
dp[t][i][j]: t ターン使って、マス(i, j) に移動するときのスコアの最大値
"""
dp = [[[-inf] * W for _ in range(H)] for _ in range(T + 1)]
dp[0][si][sj] = 0
for t in range(T):
for i in range(H):
for j in range(W):
if dp[t][i][j] == -inf:
continue
for di, dj in zip(Di, Dj):
u = i + di
v = j + dj
if not(0 <= u < H and 0 <= v < W):
continue
dp[t + 1][u][v] = max(dp[t + 1][u][v], dp[t][i][j] + A[u][v])
""" 答えを求める (移動スコア + 待機スコア) """
ans = 0
for t in range(T + 1):
for i in range(H):
for j in range(W):
ans = max(ans, dp[t][i][j] + A[i][j] * (K - t))
print(ans)あとがき
今回は ABCD 4完 15分で 1975位、1281perf でした。
2000位以内だと「良い成績取れたな~」という気持ちになるのですが、早解き回で良い成績を取れたのは初めてかもしれません。
ではまた~。


【更新履歴】
2024/06/16 (1時頃):記事投稿。
2024/06/16 (11時頃):G問題を追加。
