【ABC345】緑コーダーの競プロ参加記録 #8

今回はAtCoder Beginner Contest 345。使用言語はPythonです。

A問題 - Leftrightarrow

A - Leftrightarrow

コンテスト中の提出
https://atcoder.jp/contests/abc345/submissions/51276800

---

• <, =, > のみからなる文字列$${S}$$が与えられる。

• <==========> みたいなやつを「双方向矢印」と呼ぶ。

• $${S}$$が「双方向矢印」かどうか出力してね。

---

まず入力を受け取ります。
文字列$${S}$$の1つなのでinput関数からそのまま受け取ればよいです。

ついでに文字列$${S}$$の長さ$${N}$$も用意しておきます。len関数を使います。

""" 入力を受け取る """
S = input()

""" 問題を解く """
N = len(S)

文字列$${S}$$が双方向矢印「<====>」の形になっているか確かめたいので、まず端っこをチェックしてみます。

Pythonであれば文字列の先頭は$${S[0]}$$、末尾は$${S[-1]}$$で取得できます。末尾は$${S[N - 1]}$$でもOKです。

両端が矢印になってなければ、この時点で答えは 'No' です。

""" 入力を受け取る """
S = input()

""" 問題を解く """
N = len(S)
ans = ''
if not (S[0] == '<' and S[-1] == '>'):
    ans = 'No'

そうでなければ、端っこ以外がすべて '=' であるかチェックします。
方法はいくつかありますが、問題文にならって '=' の個数$${k}$$を数えてみます。$${k = N - 2}$$であれば答えは 'Yes' です。

""" 入力を受け取る """
S = input()

""" 問題を解く """
N = len(S)
ans = ''
if not (S[0] == '<' and S[-1] == '>'):
    ans = 'No'
else:
    k = 0
    for i in range(1, N - 1):
        if S[i] == '=':
            k += 1
    if k == N - 2:
        ans = 'Yes'
    else:
        ans = 'No'

スライスを利用して、$${S}$$の両端を除いた文字列が$${N-2}$$個の '=' であるかチェックする方法もあります。
Pythonでは文字列生成を '*' 演算子を使って行うことができます。

""" 入力を受け取る """
S = input()

""" 問題を解く """
N = len(S)
ans = ''
if not (S[0] == '<' and S[-1] == '>'):
    ans = 'No'
else:
    if S[1:-1] == '=' * (N - 2):
        ans = 'Yes'
    else:
        ans = 'No'

最初から「長さ$${N}$$の双方向矢印」を作ってしまってもよいです。
Pythonでは '+' 演算子を使って文字列を連結できます。

""" 入力を受け取る """
S = input()

""" 問題を解く """
N = len(S)
T = '<' + '=' * (N - 2) + '>'
ans = ''
if S == T:
    ans = 'Yes'
else:
    ans = 'No'

答えはprint関数で出力します。

""" 答えを出力 """
print(ans)

B問題 - Integer Division Returns

B - Integer Division Returns

コンテスト中の提出
https://atcoder.jp/contests/abc345/submissions/51279181

---

• 整数$${X}$$が与えられる。$${  (-10^{18} \leq X \leq 10^{18}) }$$

• $${\Large \lceil \frac{X}{10} \rceil}$$を出力してね。

---

Pythonでの解法

問題文がやや小難しいですが、要は「$${X}$$を10で割って切り上げした数」を答える問題です。

切り上げは標準ライブラリの math モジュールにceil関数があります。

""" ぱっと見 AC になりそうなコード """
from math import ceil
X = int(input())
ans = ceil(X / 10)
print(ans)

以上で解けました…と、言いたいのですが実はこれでは WA になります。

その原因は$${\Large\frac{X}{10}}$$の時点で小数 (float 型) を経由してしまうことで小数誤差が発生するケースがあるためです。(後述)

小数を経由しない切り捨て、切り上げは次のコードで可能です。

""" 切り捨て """
x = b // a

""" 切り上げ """
y = (b + a - 1) // a

これを利用してWAになったコードを修正します。

""" ACコード """
X = int(input())
ans = (X + 10 - 1) // 10
print(ans)

Python であれば、以上で解けました。

小数誤差について

やや極端な話をします。
たとえば$${\Large\frac{6}{2}}$$を人間が計算すると$${3}$$になりますが、これをコンピュータが計算するとfloat型の小数誤差で$${3.0000…1}$$になったりすることがあります。本来$${3}$$は切り上げしても$${3}$$なのに対して$${3.0000…1}$$だと$${4}$$になります。

実際には大きい数を扱う時に起こる現象で、浮動小数点数の精度が15桁であることに起因します。今回の問題はそれを狙って$${X \leq 10^{18}}$$の制約になっているんですね。

""" 小数誤差の例 """
from math import ceil
print(ceil(777777777777770020 / 10))

"""
>>> 77777777777777008  # ?!
"""

競プロにおいて、整数を扱う問題ではなるべく常に整数で扱うようにし、小数を経由することによる誤差を発生させないよう気を付ける必要があります。

Python以外での解法

今回の問題は$${-10^{18} \leq X}$$が認められています。

上の解法では、「切り上げ」を「(10 - 1) を足してから切り捨て除算」に置き換えて解きました。
実は、負の値に対する切り捨て除算はプログラミング言語によって挙動が異なります。

実際に、Pythonで AC となったコードを Rust で書くと WA になりました。

// Rust の WA コード
#[allow(non_snake_case)]
fn main() {
    input!{
        X: i64
    }
    let ans:i64 = (X + 9) / 10;
    println!("{}", ans)
}

こういった言語ではちょっと工夫が必要で、たとえば負の値を正の値に変換してから切り捨てするなどします。

// Rust の AC コード
#[allow(non_snake_case)]
fn main() {
    input!{
        X: i64
    }
    let mut ans: i64;
    let m: i64 = 1_000_000_000_000_000_000;
    if X >= 0{
        ans = (X + 9) / 10;
    }else{
        ans = (X + m + 9) / 10;
        ans -= m / 10;
    }
    println!("{}", ans)
}

解説用コード
https://atcoder.jp/contests/abc345/submissions/51357938

公式解説により詳しい内容が掲載されています。

---

余談ですが、負の値に対する「余り」の計算もプログラミング言語によって挙動が異なります。

C問題 - One Time Swap

C - One Time Swap

コンテスト中の提出
https://atcoder.jp/contests/abc345/submissions/51305387

---

• 文字列$${S}$$が与えられる。

• 操作: $${i < j}$$として、$${S}$$の$${i}$$文字目と$${j}$$文字目を入れ替える。

• 操作を 1回 した後の文字列としてあり得るものの個数を出力してね。

---

必ず1回は操作をしなければなりません。
そのため元の文字列$${S}$$が答えに含まれない場合もあります。

文字列 S と異なる文字列を作る

まずは文字列$${S}$$と異なる文字列を作ることにします。
つまり$${S_i \not = S_j}$$である$${(i, j)}$$について考えます。

文字列$${S}$$の長さは$${N \leq 10^6}$$であり、$${(i, j)}$$を全探索すると$${O(N^2)}$$になるので TLE してしまいます。

""" TLE !!!! """
for i in range(N):
    for j in range(i + 1, N):
        if S[i] != S[j]:
            ans += 1

ここで、$${S_i \not = S_j}$$であれば$${i}$$文字目と$${j}$$文字目を入れ替えると必ず「文字列$${S}$$と異なる」かつ「この操作でしか作れない文字列」が得られます。

よって$${i}$$を決め打ちしたとき、$${i}$$文字目より後ろに$${S_i}$$でない文字が何個あるかが分かっていればよさそうです。
文字列$${S}$$を後ろから見ていき、各アルファベットごとにDPっぽくカウントしていきます。

$$
dp[i][c]: Sのi文字目より後ろにある文字cの個数 \\
(c: a = 0, b = 1, … , y = 24, z = 25)
$$

$${a-z}$$を$${0-25}$$に対応させるのはord関数を利用するとよいです。

"""
dp[i][c]: S の i 文字目より後ろにある文字 c の個数
"""
dp = [[0] * 26 for _ in range(N + 1)]
for i in reversed(range(N)):
    for c in range(26):
        dp[i][c] = dp[i + 1][c]
        if ord(S[i]) - ord('a') == c:
            dp[i][c] += 1

あとは各$${i}$$について「$${i}$$文字目より後ろにある$${S_i}$$でない文字の個数」、すなわち$${S_i \not = c}$$である文字$${c}$$における$${dp[i][c]}$$を答えに加算し続けます。

""" S と異なる文字列の作り方 """
ans = 0
for i in range(N):
    for c in range(26):
        if ord(S[i]) - ord('a') == c:
            continue
        ans += dp[i + 1][c]

本記事では$${S_i, dp[i]}$$の$${i}$$は1-indexであるのに対して文字列$${S}$$の走査は0-indexであり、添え字のミスに注意してください。

文字列 S を作れる条件は？

$${S_i = S_j}$$であればよいです。
そして$${S_i = S_j}$$を満たす$${(i, j)}$$であればどんな選び方をしても文字列$${S}$$を作れます。

よって「文字列$${S}$$の中に$${S_i = S_j}$$である$${(i, j)}$$が存在する」、すなわち「文字列$${S}$$の中に2回以上現れる文字$${c}$$がある」場合に答えを +1 します。

""" 文字列 S を作れるか？ """
if max(dp[0][c] for c in range(26)) >= 2:
    ans += 1
print(ans)

以上で解けました。

---

公式解説では、以下の方法を取っています。

1. $${i \geq j}$$でもOKと考えて、$${(i, j)}$$の選び方は$${N^2}$$通りある。

2. $${S_i = S_j}$$である$${(i, j)}$$の選び方$${\displaystyle\sum_{c=0}^{25}cnt[c] ^ 2}$$通りを引く。

3. $${i > j}$$のパターンを除くため 2 で割る。

組み合わせで考えると、よりシンプルになる気がします。
「$${n}$$個の中から$${2}$$個選ぶ」組み合わせは$${_nC_2 = \large\frac{n(n-1)}{2}}$$通りです。

""" 公式解説の解き方(改) """
from collections import Counter
from string import ascii_lowercase
S = input()
N = len(S)
Cnt = Counter(S)
ans = N * (N - 1) // 2
for c in ascii_lowercase:
    ans -= Cnt[c] * (Cnt[c] - 1) // 2
if max(Cnt[c] for c in ascii_lowercase) >= 2:
    ans += 1
print(ans)

D問題 - Tiling

D - Tiling

コンテスト中の提出
https://atcoder.jp/contests/abc345/submissions/51339900

---

• $${H}$$行$${W}$$列のマス目と、$${N}$$枚のタイルが与えられる。

• $${i}$$枚目のタイルの大きさは$${A_i \times B_i}$$。

• タイルは回転してもOK。使わないタイルがあってもOK。

• マス目をすべて埋められるか出力してね。

---

ABC307 - C - Ideal Sheet や ABC322 - D - Polyomino と似た香りを感じます。

まずは情報の整理から

( 1 )
$${N \leq 7, H, W \leq 10}$$と、アヤシイ制約をしています。
$${N}$$はさておき、$${H \times W \leq 100}$$は「マス目を全探索してもいいよ」というメッセージとして受け取っておきます。

( 2 )
条件の中に、「使わないタイルがあってもOK」というものがあります。
つまり「あるタイルを使う/使わない」を考慮した$${2^N}$$通りのタイルの選び方があるので、bit全探索をします。

ここで$${N \leq 7}$$という制約に合点がいきます。

( 3 )
さらに「タイルを回転・裏返ししてOK」という条件もあります。
ここで「マス目に沿って置いてね」という条件から回転は90度ごとに限定されます。

タイルが$${A \times B}$$の長方形であることを考えると、どれだけ回転・裏返しをしても$${A \times B}$$か$${B \times A}$$の2パターンしかありません。

よって$${i}$$枚のタイルを使うことを決めたとき、「タテ/ヨコ」を考慮した$${2^i}$$通りのタイルの置き方があるので、これもbit全探索します。

---

問題文から読み取れるのはこのあたりでしょうか。
現時点で計算量が$${HW \times \displaystyle\sum_{i=1}^N  (_NC_i \times 2^i)}$$くらいありそうです。

$${N = 7, H = 10, W = 10}$$だと$${218,600}$$です。意外と小さい。

""" 現時点での 全体のイメージ """
N, H, W = map(int, input().split())
T = [tuple(map(int, input().split())) for _ in range(N)]

for choice in range(1, 1 << N):
    tiles = get_tiles(choice)
    M = len(tiles)
    for spin in range(1 << M):
        if completed(tiles, spin):
            print('Yes')
            exit()
print('No')

タイルはどう置けばよい？

使うタイルの選び方、各タイルの向きが決まったところで、タイルをどこに配置するかはどのように決めればいいのでしょう。
ここがこの問題の難しいポイントです。

タイルの置き場所をやみくもに全探索しようとすると計算量が膨れ上がってしまいそうです。

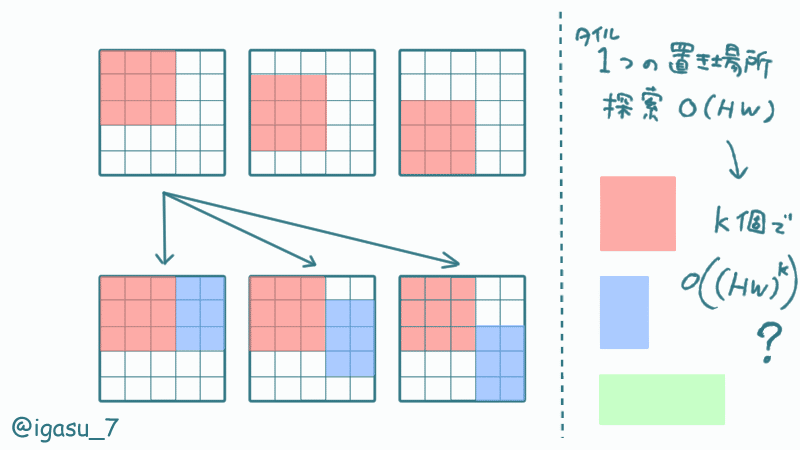
左上から貪欲に置くだけで済むなら楽なのになぁ。

・・・

ここで、問題ページに添付されている図を眺めてみます。

これを左上から貪欲に置いた結果だと捉えると、$${2 \rarr 4 \rarr 5}$$の順番で配置したことになります。その他に$${5 \rarr 4 \rarr 2}$$の順番でも条件を満たせそうですが$${2 \rarr 5 \rarr 4}$$と置くとタイル$${5}$$がはみ出てしまいます。

タイルの選び方、向き、置く順番のすべてが正しければ貪欲に置いても条件を満たす配置を実現できそうです。
（正直上手く説明できません。フィーリングです。）

公式解説では「タイル配置が決まっているとき各タイルを置く順番がどうであれ答えは変わらないので、勝手に順番を決めてよい」となっています。

ということで、タイルを置く順番を決めてみます。
順番の決め方は、選んだタイルを横一列に並べる方法と同じであり、これはまさに順列のことを指しています。

あり得る順番をすべて試すため順列全探索をします。
$${i}$$枚のタイルを選んだ時、その順番の決め方は$${i!}$$通りあります。

""" 現時点での 全体のイメージ """
from itertools import permutations
N, H, W = map(int, input().split())
T = [tuple(map(int, input().split())) for _ in range(N)]

for choice in range(1, 1 << N):
    tiles = get_tiles(choice)
    M = len(tiles)
    for perm in permutations(tiles):
        for spin in range(1 << M):
            if completed(perm, spin):
                print('Yes')
                exit()
print('No')

現時点で計算量が$${HW \times \displaystyle\sum_{i=1}^N  (_NC_i \times 2^i \times i!)}$$くらいありそうです。

$${N = 7, H = 10, W = 10}$$だと$${106,362,200}$$です。

これに定数倍かかると間に合うか不安ですが、枝刈りでなんとかなることを祈ります。

後は、がんばる。

解説用コードの全体
https://atcoder.jp/contests/abc345/submissions/51425162

bit全探索で使うタイルを選ぶのは、ビットマスクの$${k}$$桁目が 1 になっているときにタイル$${k}$$を選べばよいです。

def get_tiles(mask: int):
    """ 使うタイルを選ぶ """
    tiles = []
    for k in range(N):
        if (mask >> k) & 1 == 1:
            tiles.append(T[k])
    return tiles

この選んだタイルについて順番と回転の方法を決めて、条件を満たすことができるか試します。
タイルの回転は、ビットマスクの$${k}$$桁目が 1 になっているときに$${A, B}$$を$${B, A}$$に置き換えればよいです。

def completed(perm: tuple[int, int], mask: int):
    """ タイルを順番に配置して、マス目を埋められるか判定 """
    used = [[False] * W for _ in range(H)]
    k = 0
    for i in range(H):
        for j in range(W):
            if used[i][j]:
                continue
            if k >= len(perm):
                return False
            h, w = perm[k]
            if (mask >> k) & 1 == 1:
                h, w = w, h
            k += 1
            if not(i + h <= H and j + w <= W):
                return False
            for u in range(i, i + h):
                for v in range(j, j + w):
                    if used[u][v]:
                        return False
                    used[u][v] = True
    return True

以下の条件に注意してください。

• マス目をはみ出してはいけない。

• 他のタイルと重なってはいけない。

• 同じタイルを使ってはいけない。

• 空きマスが残ってはいけない。

条件を満たす配置パターンが1つでも見つかったとき 'Yes' を出力してプログラムを停止するようにしていれば 2 sec に間に合います。
PyPy で 1200 ms 程度です。

---

解説用コードの全体 (2)
https://atcoder.jp/contests/abc345/submissions/51422796

選んだタイルの面積の総和が$${HW}$$と一致しない場合は明らかに条件を満たすことができません。

def different_size(tiles: list[tuple[int, int]]):
    """ 選んだタイルとマス目のサイズが同じかどうか判定 """
    s = 0
    for a, b in tiles:
        s += a * b
    return s != H * W

# 略

for choice in range(1, 1 << N):
    tiles = get_tiles(choice)
    if different_size(tiles):
        continue
    
    # 略

この枝刈りをしていると PyPy で 300 ms、CPython でも 1200 ms 程度です。

解説はここまでです。ありがとうございました。

E問題 - Colorful Subsequence

E - Colorful Subsequence

$$
\Huge 　 diff 2356 　
$$

あとがき

今回のコンテストの結果はABCD4完、順位は1178位、1487 perf でした。

D問題を解けたのはえらい。

ABC343, 344, ARC173で減らした分を回収しました。
翌日のARC174で同じ分だけ消し飛びましたけども。

ではまた～。

Contest Result - AtCoder