
【ABC357】緑コーダーの競プロ参加記録 #22
今回はAtCoder Beginner Contest 357。使用言語はPythonです。

A問題 - Sanitize Hands
コンテスト中の提出
https://atcoder.jp/contests/abc357/submissions/54323110
$${N}$$人の宇宙人と、$${M}$$本の手に使える消毒液がある。
$${i}$$人目の宇宙人は$${H_i}$$本の手がある。
最大で何人目まで手を消毒できるか出力してね。
消毒の順番が決まっており、「最大で何人が消毒できるか」でないことに注意が必要です。
1人目から順に、これまで消毒した手の本数の合計を記録しつつ、$${i}$$番目の人が$${H_i}$$本の手をすべて消毒できるか if 文で判定します。
""" AC コード """
N, M = map(int, input().split())
H = list(map(int, input().split()))
total = 0
ans = 0
for h in H:
if total + h > M:
break
total += h
ans += 1
print(ans)B問題 - Uppercase and Lowercase
コンテスト中の提出
https://atcoder.jp/contests/abc357/submissions/54328570
奇数の長さの文字列$${S}$$が与えられる。
操作 A: 大文字の方が多いなら、すべて大文字に変換。
操作 B: 小文字の方が多いなら、すべて小文字に変換。
操作をしたあとの$${S}$$を出力してね。
文字列$${S}$$の長さを$${N}$$とします。
また、$${S}$$に含まれる大文字の個数を$${U}$$、小文字の個数を$${L}$$とします。
$${N}$$は奇数なので、$${U = L}$$にはなりません。
$${S}$$に含まれる文字を1つずつチェックして、$${U, L}$$を特定します。
大文字 / 小文字の判定は、$${S}$$の$${i}$$文字目に対して「(1) 大文字 / 小文字の羅列のどちらに含まれているか」または「(2) isupper メソッド / islower メソッド」で行うことができます。
""" 大文字 / 小文字 の判定 (1) """
S = input()
N = len(S)
lower_case = "abcdefghijklmnopqrstuvwxyz"
upper_case = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
U, L = 0, 0
for i in range(N):
if S[i] in upper_case:
U += 1
if S[i] in lower_case:
L += 1""" 大文字 / 小文字 の判定 (2) """
S = input()
N = len(S)
U, L = 0, 0
for i in range(N)
if S[i].isupper():
U += 1
if S[i].islower():
L += 1出力時の大文字 / 小文字の変換は、upper メソッド / lower メソッドを使います。
""" 答えを出力 """
if U > L:
print(S.upper())
else:
print(S.lower())なお、「大文字 / 小文字の羅列」は手入力で用意してもよいですが、Python の標準ライブラリに用意されています。
""" 英大文字 / 英小文字 """
from string import ascii_lowercase, ascii_uppercase
print(ascii_lowercase)
print(ascii_uppercase)
"""
>>> abcdefghijklmnopqrstuvwxyz
>>> ABCDEFGHIJKLMNOPQRSTUVWXYZ
"""C問題 - Sierpinski carpet
コンテスト中の提出
https://atcoder.jp/contests/abc357/submissions/54377075
レベル$${0}$$のカーペットは黒マスからなる$${1 \times 1}$$のグリッド。
レベル$${K}$$のカーペットは$${3^{K-1} \times 3^{K-1}}$$の9ブロックで構成され、中央は白マス、中央以外はレベル$${K - 1}$$のカーペット。
レベル$${N}$$のカーペット出力してね。
どのレベルのカーペットも「9つのブロックに分けて~」という同じ操作を繰り返すことで作られています。
つまり、すべてのレベルのカーペットは規則的に並んでいます。
よって、レベル$${N}$$のカーペットに含まれるレベル$${k}$$のカーペットを全て1つずつ作っていけばよいです。
レベル$${N}$$のカーペットに含まれるレベル$${k}$$のカーペットについて情報を整理します。
レベル$${k}$$のカーペットの1辺の大きさは$${\mathrm{size} = 3^k}$$。
レベル$${k}$$のカーペットを一列に並べたとき、その個数は$${\mathrm{cnt} = \Large{\frac{3^N}{\mathrm{size}}}}$$。
レベル$${k}$$のカーペットのうち、上から$${x}$$番目、左から$${y}$$番目であるものの左上のマスの座標は$${(\mathrm{size} \times x, \mathrm{size} \times y)}$$。$${(x, y \ge 0)}$$
レベル$${k}$$のカーペットを9ブロックに分割したときの、1ブロックの1辺の大きさは$${\mathrm{sub} = \Large{\frac{\mathrm{size}}{3}}}$$。
レベル$${k}$$のカーペットを9ブロックに分割したときの、中央のものはすべて白マス。

あとは、これをコードに落とし込みます。
最初、カーペットのすべてのマスを黒マスとして初期化しておきます。
9ブロックに分割したときの中央ブロックを白マスに変更することで、問題を解くことができます。
""" AC コード """
def solve():
grid = [['#'] * pow(3, N) for _ in range(pow(3, N))]
for level in range(N + 1):
size = pow(3, level) # レベル = level の1辺の大きさ
cnt = pow(3, N) // size # レベル = level の個数
sub = size // 3 # 9分割したサブブロックの1辺の大きさ
for x in range(cnt):
for y in range(cnt):
"""
レベル = level のカーペット のうち、
上から x 番目、左から y 番目の 左上の座標 (xi, yj)
"""
xi = size * x
yj = size * y
"""
レベル = level のカーペットを 9 分割したときの、
中央ブロックの左上の座標 (si, sj)
"""
si = xi + sub
sj = yj + sub
for i in range(si, si + sub):
for j in range(sj, sj + sub):
grid[i][j] = '.'
return grid
N = int(input())
ans = solve()
for row in ans:
print(''.join(row))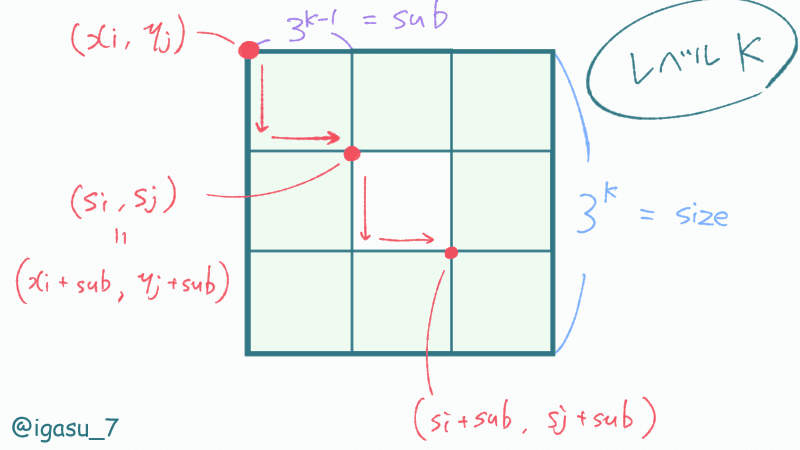
また、左上の座標を$${(i, j)}$$とするレベル$${k}$$のカーペットを作る関数を再帰的に使うと、よりシンプルな実装になります。
こちらは最初、カーペットのすべてのマスを白マスとして初期化しておきます。
""" 再帰で実装 """
from sys import setrecursionlimit
setrecursionlimit(100100100)
def dfs(i, j, level):
""" 左上の座標を (i, j) とするレベル = level のカーペットを描画 """
if level == 0:
ans[i][j] = '#'
return
size = pow(3, level)
sub = size // 3
for x in range(3):
for y in range(3):
if (x, y) != (1, 1):
xi = i + sub * x
yj = j + sub * y
dfs(xi, yj, level - 1)
N = int(input())
ans = [['.'] * pow(3, N) for _ in range(pow(3, N))]
dfs(0, 0, N)
for a in ans:
print(''.join(a))D問題 - 88888888
コンテスト中の提出
https://atcoder.jp/contests/abc357/submissions/54357757
正整数$${N}$$が与えられる。
$${N}$$を$${N}$$個繋げた整数を$${V_N}$$とする。
$${V_N \pmod{998244353}}$$を出力してね。
$${N}$$の桁数を$${k}$$とします。
すると、$${V_N}$$は以下のようになります。

$$
V_N = N + N \times 10^k +N \times 10^{2k}+N \times 10^{3k} + \dots +N \times 10^{(N - 1)k} \\
\rArr V_N = \displaystyle\sum_{i = 1}^{N} N \times (10^k)^{i-1}
$$
これは初項 $${N}$$、公比$${10^k}$$、項数$${N}$$の等比数列の和になります。
Google検索をすると公式が出てきます。
$$
\displaystyle\sum_{i = 1}^{n} a \times r^{i-1} = \frac{a(r^n - 1)}{r -1} \\
\rArr \displaystyle\sum_{i = 1}^{N} N \times (10^k)^{i-1} = \frac{N((10^k)^N - 1)}{10^k -1}
$$
$${\mathrm{mod}}$$の世界なので、分数の計算をするために逆元を求める必要があります。
Python ならpow関数の第2引数を$${ -1}$$ にするだけで求まります。
""" AC コード """
N = int(input())
mod = 998244353
k = len(str(N))
r = pow(10, k, mod)
inv = pow(r - 1, -1, mod)
ans = N * (pow(r, N, mod) - 1) % mod * inv % mod
print(ans)等比数列の和の公式の分母が$${r- 1}$$になっていますが、公式解説によると今回は$${r - 1 = 0}$$になることはないそうです。
下記のようなコードは TLE になります。
""" TLE コード """
N = int(input())
mod = 998244353
k = len(str(N))
r = 10 ** k % mod
inv = pow(r - 1, -1, mod)
ans = N * (r ** N % mod - 1) * inv % mod
print(ans)Python では int の上限がありませんが、大きすぎる数の計算にはとても時間がかかります。
累乗を計算する際、'**' 演算子を使うと$${\mathrm{mod}}$$をとる前に一度大きすぎる数を経由します。
一方で、pow 関数は計算過程で都度$${\mathrm{mod}}$$をとることで大きすぎる数が発生しないため、TLEになりません。
E問題 - Reachability in Functional Graph
upsolve
https://atcoder.jp/contests/abc357/submissions/54394963
$${N}$$頂点$${N}$$辺の有向グラフが与えられる。
すべての頂点の出次数は$${1}$$。
頂点$${i}$$から頂点$${A_i}$$に辺が伸びている。
頂点$${u}$$から頂点$${v}$$に到達可能な$${(u, v)}$$の個数を出力してね。
考察
「$${N}$$頂点$${N}$$辺、全ての頂点の出次数$${1}$$」という条件から、このグラフの各連結成分としてありうる形は以下の2パターンです。

まず、サイクルの中では任意の頂点間を移動可能です。
よって、サイクルの頂点数を$${C}$$とすると、サイクル内のある頂点から到達可能な頂点数は$${C}$$になります。
次に、サイクルでない部分に着目します。
「あるサイクル内の頂点$${y}$$」から1つ離れたところにある「サイクル外の頂点$${x}$$」を考えます。($${A_x = y}$$)
このとき、頂点$${x}$$から到達可能な頂点数は$${C + 1}$$になります。(サイクル + $${x}$$自身。)
同様に、頂点$${x}$$に辺を伸ばしている、すなわち$${A_i = x}$$である頂点$${i}$$について、頂点$${i}$$から到達可能な頂点数は$${(C + 1) + 1}$$になります。($${x}$$から到達可能 + $${i}$$自身。)
このことから、サイクルでない部分のうちサイクルに近い方の頂点から順に、到達可能な頂点数をカウントすることができます。

問題を解く
入次数$${0}$$の頂点から探索を始めて、到達した頂点$${i}$$について頂点$${A_i}$$の入次数を$${-1}$$し、入次数が$${0}$$になれば探索候補に追加することを繰り返します。
(トポロジカルソートのような動きになります。)
サイクルに含まれる頂点の入次数が$${0}$$になることはありません。
これによって、「サイクルでない部分」の頂点を「サイクルに1つずつ近づくような順番」で探索できます。
探索順を維持したまま、探索した頂点を記録しておきます。(後述)
""" 入力を受け取る (0-index に変換) """
N = int(input())
A = list(map(lambda x: int(x) - 1, input().split()))
""" 入次数を調べる """
Cnt = [0] * N
for a in A:
Cnt[a] += 1
roots = []
for i in range(N):
if Cnt[i] == 0:
roots.append(i)
""" サイクルでない部分のみを探索する """
seen = [False] * N
acyclic = []
while roots:
curr = roots.pop()
seen[curr] = True
nxt = A[curr]
if not seen[nxt]:
Cnt[nxt] -= 1
if Cnt[nxt] == 0:
roots.append(nxt)
acyclic.append(curr)次に、サイクル部分を探索してサイクルの頂点数を求めます。
頂点$${i}$$から到達可能な頂点数を$${\mathrm{res}[i]}$$とします。
""" サイクル部分のサイズと、到達可能な頂点数をカウント """
res = [0] * N
for i in range(N):
if seen[i]:
continue
curr = i
cycle_size = 0
while not seen[curr]:
seen[curr] = True
curr = A[curr]
cycle_size += 1
for _ in range(cycle_size):
res[curr] = cycle_size
curr = A[curr]最後に、「サイクルでない部分」の頂点を「サイクルから1つずつ離れていくような順番」で探索します。
つまり、サイクル内の頂点を始点として、与えられた辺の向きと逆向きに処理を進めます。
これは、「サイクルでない部分」の頂点を「サイクルに1つずつ近づくような順番」で記録したリストを逆から見ていくことで実現できます。
""" サイクルでない部分の、到達可能な頂点数をカウント """
while acyclic:
curr = acyclic.pop()
nxt = A[curr]
res[curr] = res[nxt] + 1
""" 答えを出力 """
ans = sum(res)
print(ans)あとがき
今回は ABCD 4完 1ペナ 104分で 3344位、981 perf でした。
C問題が苦手すぎて解くのに合計80分かかりました・・・。
いったん飛ばしてD問題に進んだのはよかったです。
終了後に「C問題を解かずにE問題に進んでればよかったなぁ」と思ったものの、ふつうに実装に困ったのでC問題に戻って正解でした。
ではまた~。

【更新履歴】
2024/06/09 (15時頃):記事投稿。
