
【ABC353】緑コーダーの競プロ参加記録 #17
今回はAtCoder Beginner Contest 353。使用言語はPythonです。

A問題 - Buildings
コンテスト中の提出
https://atcoder.jp/contests/abc353/submissions/53322799
$${N}$$個のビルがある。
$${i}$$番目のビルの高さは$${H_i}$$。
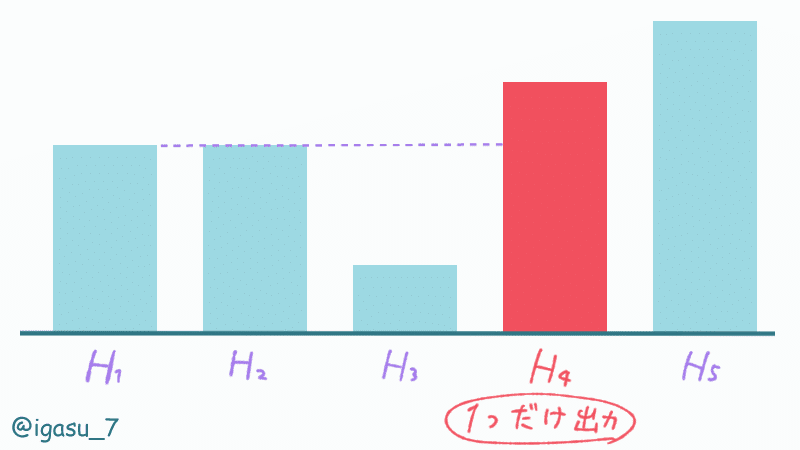
$${1}$$番目のビルより高い最初のビルは何番目か出力してね。
$${H_1 < H_i}$$となる最初の$${i}$$を出力すればよく、そのような$${i}$$がなければ答えは -1 です。
リストを全探索するときは 0-index で出力は 1-index になること、2つ以上の出力をしないことに注意が必要です。
""" ACコード """
N = int(input())
H = list(map(int, input().split()))
for i in range(1, N):
if H[0] < H[i]:
print(i + 1)
exit()
print(-1)B問題 - AtCoder Amusement Park
コンテスト中の提出
https://atcoder.jp/contests/abc353/submissions/53329932
$${K}$$人乗りのアトラクションと$${N}$$組のグループがある。
$${i}$$番目のグループは$${A_i}$$人。
$${i=1}$$から$${i=N}$$まで順番に操作を繰り返す。
操作: グループ単位で可能な限り乗せてスタートする。
何回アトラクションをスタートさせるか出力してね。
問題文が長く読むのが大変ですが、問題文に書かれてあることを丁寧にコードになおしていけばよいです。入力例1の図も参考になります。
$${1 \le N, K \le 100}$$なのでシンプルな実装で 2 sec に間に合います。
""" ACコード """
N, K = map(int, input().split())
A = list(map(int, input().split()))
ans = 0
B = 0
i = 0
while i < N:
while i < N and B + A[i] <= K:
B += A[i]
i += 1
ans += 1
B = 0
print(ans)上記のような while ループではなく、for ループを使って解くこともできます。
その際、最後のグループが取り残されるので答えを +1 することに注意が必要です。
""" 別解 """
N, K = map(int, input().split())
A = list(map(int, input().split()))
ans = 0
B = 0
for i in range(N):
if B + A[i] <= K:
B += A[i]
else:
ans += 1
B = A[i]
ans += 1
print(ans)C問題 - Sigma Problem
コンテスト中の提出
https://atcoder.jp/contests/abc353/submissions/53355538
$${f(x, y)}$$は「$${x + y}$$を$${10^8}$$で割った余り」。
$${\displaystyle\sum_{i =1}^{N-1}\displaystyle\sum_{j=i+1}^Nf(A_i,A_j)}$$を出力してね。
式に表れているように、素直に解こうとすると$${O(N^2)}$$であり TLE になってしまいます。
和が小さい場合
たとえば、どの$${(A_i, A_j)}$$のペアを選んだとしてもその和が$${10^8}$$未満であるとします。
つまり、$${f(A_i, A_j) = A_i + A_j}$$です。
ある$${i}$$に対しては、$${i < j}$$である$${N - i}$$個の$${(i, j)}$$のペアを作ることができます。
このとき、答えに加算する値は以下のようになります。
$$
\displaystyle\sum_{j =i+1}^N (A_i + A_j) \\
= (N - i) \times A_i +\displaystyle\sum_{j =i+1}^N A_j
$$
$${\displaystyle\sum_{j =i+1}^N A_j}$$は累積和を用いて$${O(1)}$$で計算できます。

【補足】
$$
\displaystyle\sum_{j =i+1}^N (A_i + A_j)
$$
上式は「$${i + 1 \le j \le N}$$を満たす$${j}$$における$${A_i + A_j}$$の総和」を意味しています。
$${i + 1 \le j \le N}$$を満たす$${j}$$の個数は$${N - i}$$です。
たとえば$${i = 3, N = 8}$$とすると$${j}$$の候補は$${{4, 5,6,7,8}}$$の5個になります。
ここで、上式は次のように分解できます。
$$
\displaystyle\sum_{j =i+1}^N (A_i + A_j) = \displaystyle\sum_{j =i+1}^N A_i + \displaystyle\sum_{j =i+1}^N A_j
$$
また、$${\displaystyle\sum_{j =i+1}^N}$$の中で動く値は$${j}$$であり、$${i}$$は関係ありません。
よって、以下が成り立ちます。
$$
\displaystyle\sum_{j =i+1}^N A_i = (N - i) \times A_i
$$
この手順で、先に述べた式が出てきます。
$$
\displaystyle\sum_{j =i+1}^N (A_i + A_j) \\
= (N - i) \times A_i +\displaystyle\sum_{j =i+1}^N A_j
$$
和が大きい場合
次に、どの$${(A_i, A_j)}$$のペアを選んだとしてもその和が$${10^8}$$以上であるとします。
$${1 \le A_i < 10^8}$$より、$${A_i + A_j}$$の最大値は$${2 \times 10^8 - 2}$$です。
つまり、$${A_i + A_j (\mathrm{mod} 10^8)}$$と$${A_i + A_j - 10^8}$$が同じ意味になります。
ある$${i}$$に対して、答えに加算する値は以下のようになります。
$$
\displaystyle\sum_{j =i+1}^N (A_i + A_j - 10^8) \\
= (N - i) \times (A_i - 10^8) +\displaystyle\sum_{j =i+1}^N A_j
$$

問題を解く
ある$${i}$$について、以下のように$${p, q}$$を定めます。
$${A_i + A_j < 10^8}$$かつ$${i < j}$$である$${j}$$の個数を$${p}$$
$${A_i + A_j \ge 10^8}$$かつ$${i < j}$$である$${j}$$の個数を$${q}$$
このとき$${p + q = N - i}$$であり、答えに加算する値は以下のようになります。
$$
\displaystyle\sum_{i =j+1}^N f(A_i, A_j) \\
= p \times A_i +q \times (A_i - 10^8) +\displaystyle\sum_{j =i+1}^N A_j \\
= (N - i) \times A_i - q \times 10^8 +\displaystyle\sum_{j =i+1}^N A_j \\
$$
ここで、$${f(A_i, A_j) = f(A_j, A_i)}$$なので$${A}$$をソートしても問題ありません。
また、ソート後の$${A}$$に対して$${10^8 - A_i}$$を二分探索をすることで$${q}$$を高速に求めることができます。

以下のコードでは累積和を itertools.accumulate、二分探索を bisect.bisect_left で行っています。
bisect_left で得られる$${j}$$について常に$${i < j}$$とならないことに注意してください。
from itertools import accumulate
from bisect import bisect_left
mod = 10 ** 8
""" ソートして累積和 """
N = int(input())
A = list(map(int, input().split()))
A.sort()
acc = list(accumulate(A))
""" 二分探索して足したり引いたり """
ans = 0
for i in range(N):
j = bisect_left(A, mod - A[i])
q = N - max(i + 1, j)
ans += acc[N - 1] - acc[i]
ans += (N - i - 1) * A[i]
ans -= mod * q
print(ans)この解法は ABC351- E - Jump Distance Sum や ABC351- F - Double Sum の部分問題に似ています。
公式解説と異なる解法なので、分かりやすいと思う方を参考にしてみてください。
D問題 - Another Sigma Problem
コンテスト中の提出
https://atcoder.jp/contests/abc353/submissions/53369939
$${f(x,y)}$$は「$${\mathrm{str}(x) + \mathrm{str}(y)}$$ を整数とみなした値」。
$${\displaystyle\sum_{i =1}^{N-1}\displaystyle\sum_{j=i+1}^Nf(A_i,A_j) }$$を出力してね。$${(\mathrm{mod} 998244353)}$$
C問題と異なり$${f(A_i, A_j) \not= f(A_j,A_i)}$$なので、$${A}$$をソートできません。
$${y}$$の桁数を$${k}$$とすると、$${f(x, y) = x \times 10^k + y}$$です。
$${1 \le A_i \le 10^9}$$より、$${1 \le k \le 10}$$です。

C問題と同様、$${f(x, y)}$$をシンプルな和の形に直せたので、$${x \times 10^k}$$と$${y}$$を独立して計算できるようになりました。
ここで、ある$${i}$$について、$${A_i}$$が$${x}$$になるパターンと$${y}$$になるパターンの2つが考えられます。
それぞれについて、答えに加算する値は以下のようになります。
$${A_i}$$が$${x}$$になるパターンでは$${A_i \times 10^k}$$
$${A_i}$$が$${y}$$になるパターンでは$${A_i}$$

$${A_i}$$が$${y}$$になるパターンは$${i - 1}$$個あります。
$${A_i}$$が$${x}$$になるパターンは$${N - i}$$個ありますが、$${y}$$の桁数によって加算する値が変わります。
ある$${i}$$について、$${i < j}$$を満たす$${A_j}$$のうち$${k}$$桁のものがいくつあるか分かっている必要がありそうです。
""" cnt[i][k]: A の i 番目以降に k 桁の整数がいくつあるか """
N = int(input())
A = list(map(int, input().split()))
cnt = [[0] * 11 for _ in range(N + 1)]
for i in reversed(range(N)):
d = len(str(A[i]))
cnt[i][d] += 1
for k in range(11):
cnt[i][k] += cnt[i + 1][k]$${y}$$の桁数$${k}$$を考えることで、ある$${i}$$を固定したとき$${j}$$の候補の探索を$${O(N)}$$から$${O(10)}$$程度まで減らせました。
""" A_i が x, y になるパターンを分けて加算 """
mod = 998244353
ans = 0
for i in range(N):
y = A[i]
ans += y * i
for k in range(11):
x = A[i] * pow(10, k)
ans += x * cnt[i + 1][k]
ans %= mod
print(ans)今回の制約では$${f(A_i, A_j) \le 10000000001000000000}$$であり、答えは最大でも$${_NC_2 \times 10000000001000000000 \le 10^{30}}$$程度なので、$${\mathrm{mod}}$$の計算は最後に行うだけでもよいです。
一般的には、$${\mathrm{mod}}$$の計算は都度行う方がよいです。
Python の int にオーバーフローはありませんが、大きすぎる数の計算には時間がかかるので TLE の原因になります。
""" mod の計算を都度行う """
mod = 998244353
ans = 0
for i in range(N):
y = A[i]
ans += y * i % mod
ans %= mod
for k in range(11):
x = A[i] * pow(10, k) % mod
ans += x * cnt[i + 1][k] % mod
ans %= mod
print(ans)E問題 - Yet Another Sigma Problem
upsolve
https://atcoder.jp/contests/abc353/submissions/53385473
$${f(x,y)}$$は「$${x, y}$$ の最長共通接頭辞の長さ」。
$${\displaystyle\sum_{i =1}^{N-1}\displaystyle\sum_{j=i+1}^Nf(S_i,S_j) }$$を出力してね。
公式解説にあるTrie木というものが分からないので独自の解法になります。
$${S}$$の各文字列を1文字目が「'a' のグループ」「'b' のグループ」…「'z' のグループ」に分けてみます。
異なるグループ間の$${f(S_i, S_j)}$$は$${0}$$になります。
1文字目が「'a' のグループ」の中ではどの$${(S_i, S_j)}$$を選んだとしても1文字目が共通接頭辞になるので、「'a' のグループ」のサイズを$${M}$$とすると、答えに加算する値は$${_MC_2}$$です。
次に、1文字目が「'a' のグループ」の文字列すべてから1文字目を削除したものとして、そのグループをさらに1文字目が「'a' のグループ」「'b' のグループ」…「'z' のグループ」に分けてみます。
これを繰り返せばよさそうです。再帰関数が使えます。

$${S}$$をソートすると接頭辞を考えやすくなります。
次のグループのサイズが$${2}$$以上の場合のみ処理を進めるなどの枝刈りをすることで 2 sec に間に合います。
""" ちょっとムリヤリかもしれない解法 """
from collections import deque
from sys import setrecursionlimit
setrecursionlimit(100100100)
""" グループ curr の k 文字目を考える """
def solve(curr, k):
global ans
i = 0
for c in range(26):
nxt = []
while i < len(curr):
s = curr[i]
if len(s) <= k:
i += 1
continue
if ord(s[k]) - ord('a') == c:
nxt.append(s)
i += 1
else:
break
M = len(nxt)
if M >= 2:
ans += M * (M - 1) // 2
solve(nxt, k + 1)
N = int(input())
S = input().split()
S.sort()
ans = 0
solve(S, 0)
print(ans)再帰関数を使っていますが、PyPy でも AC になります。
あとがき
今回はABCD 4完 81分 で 2966位、1051 perf でした。
A - E でC問題がいちばん難しかったまである。
問題文を見て「ABC351 - Eでつまづいたやつだ!」となったのと同時に「あれ青diffだったよね…?」ともなりました。
ABC351 - Eを解いてなければ今回の C も解けてなかったと思います。
ではまた~。

【更新履歴】
2024/05/12 (13時頃):記事投稿。
2024/05/12 (17時頃):E問題の掲載コード、一部文章を修正。
